图是不同于树的另一种非线性数据结构。在树结构中,数据元素之间存在着一种层次结构的关系,每一层上的数据元素可以和下一层的多个数据元素相关,但只能和上一层的单个数据元素相关。也就是说,树结构的数据元素之间是一种一对多的关系;在图结构中,数据元素之间的关系则是多对多的关系。即图中的每个数据元素可以和图中任意别的数据元素相关,所以图是一种比树更复杂的数据结构。
树结构可以看做是图的一种特例。
图的逻辑结构
图的定义和常用术语
图是一系列顶点(结点)和描述顶点之间的关系边(弧)组成。图是数据元素的集合,这些数据元素相互连接形成网络。其形式化定义为:G=(V,E)。其中,G表示图,V是顶点的集合,E是边或弧的集合。并且E可以表示为:E=(Vi,Vj),表示顶点Vi和Vj之间有边或弧相连。
- 顶点集:图中具有相同特性的数据元素的集合;
- 边(弧):边是一对顶点间的路径,通常带箭头的边称为弧;
- 弧头、弧尾
- 度:在无向图中顶点的度是指连接那个顶点的边的数目。在有向图中,每个顶点有两种类型的度(入度、出度);
- 入度:指向那个顶点的边的数目;
- 出度:由那个顶点出发的边的数目;
- 权:有些图的边或弧附带有一些数据信息,这些数据信息称为边或弧的权。在实际问题中,权可以表示某种含义,比如在一个地方的交通图上,边上的权值表示该条线路的长度。
图的分类
- 有向图:在一个图中,如果任意两顶点构成的偶对(如果存在)是有序的,那么称该图为有向图;
- 无向图:在一个图中,如果任意两顶点构成的偶对(如果存在)是无序的,那么称该图为无向图;
- 有向完全图:在一个有向图中,如果任意两个顶点之间都是有弧相连,则称该图是完全有向图;
- 有向完全图:在一个无向图中,如果任意两个顶点之间都是有边相连,则称该图是完全无向图;
- 稀疏图:有很少条边或弧的图;
- 稠密图:有很多条边或弧的图。
图的抽象数据类型
- 数据元素:具有相同元素(结点)的数据集合;
- 数据结构:结点之间通过边或弧相互连接形成网络;
- 数据操作:对图的基本操作定义在IGraph中,代码如下:
public interface IGraph<E> {public int getNumOfVertex();//获取顶点的个数boolean insertVex(E v);//插入顶点boolean deleteVex(E v);//删除顶点int indexOfVex(E v);//定位顶点的位置E valueOfVex(int v);// 定位指定位置的顶点boolean insertEdge(int v1, int v2,int weight);//插入边boolean deleteEdge(int v1, int v2);//删除边int getEdge(int v1,int v2);//查找边String depthFirstSearch(int v );//深度优先搜索遍历String breadFirstSearch(int v );//广度优先搜索遍历public int[] dijkstra(int v);//查找源点到其它顶点的路径
}
图的实现
由图的定义可知,一个图的信息主要包括两部分,图中顶点的信息以及描述顶点之间的关系——边或弧的信息。邻接矩阵和邻接表是图的两种最通用的存储结构。
邻接矩阵
邻接矩阵是用两个数组来表示图,一个数组是一维数组,存储图中的顶点信息;一个数组是二维数组,即矩阵,存储顶点之间相邻的信息,也就是边或弧的信息。如果图中有n个顶点,就需要n×n的二维数组来表示图。
- 如果图的边没有权值,用0表示顶点之间无边,用1表示顶点之间有边。
- 如果图的弧有权值,用无穷大表示顶点之间无边,用权值表示顶点之间有边,同一点之间的权值为0。
注意:如果图为稀疏图的话,在用邻接矩阵表示图的时候,由于在表示边的时候会导致变成一个系数矩阵,导致很多的浪费。所以,应在图为稠密图的时候使用邻接矩阵实现图。
public class GraphAdjMatrix<E> implements IGraph<E> {private E[] vexs;// 存储图的顶点的一维数组private int[][] edges;// 存储图的边的二维数组private int numOfVexs;// 顶点的实际数量private int maxNumOfVexs;// 顶点的最大数量private boolean[] visited;// 判断顶点是否被访问过@SuppressWarnings("unchecked")public GraphAdjMatrix(int maxNumOfVexs, Class<E> type) {this.maxNumOfVexs = maxNumOfVexs;edges = new int[maxNumOfVexs][maxNumOfVexs];vexs = (E[]) Array.newInstance(type, maxNumOfVexs);}// 得到顶点的数目public int getNumOfVertex() {return numOfVexs;}// 插入顶点public boolean insertVex(E v) {if (numOfVexs >= maxNumOfVexs)return false;vexs[numOfVexs++] = v;return true;}// 删除顶点public boolean deleteVex(E v) {for (int i = 0; i < numOfVexs; i++) {if (vexs[i].equals(v)) {for (int j = i; j < numOfVexs - 1; j++) {vexs[j] = vexs[j + 1];}vexs[numOfVexs - 1] = null;for (int col = i; col < numOfVexs - 1; col++) {for (int row = 0; row < numOfVexs; row++) {edges[col][row] = edges[col + 1][row];}}for (int row = i; row < numOfVexs - 1; row++) {for (int col = 0; col < numOfVexs; col++) {edges[col][row] = edges[col][row + 1];}}numOfVexs--;return true;}}return false;}// 定位顶点的位置public int indexOfVex(E v) {for (int i = 0; i < numOfVexs; i++) {if (vexs[i].equals(v)) {return i;}}return -1;}// 定位指定位置的顶点public E valueOfVex(int v) {if (v < 0 ||v >= numOfVexs )return null;return vexs[v];}// 插入边public boolean insertEdge(int v1, int v2, int weight) {if (v1 < 0 || v2 < 0 || v1 >= numOfVexs || v2 >= numOfVexs)throw new ArrayIndexOutOfBoundsException();edges[v1][v2] = weight;edges[v2][v1] = weight;return true;}// 删除边public boolean deleteEdge(int v1, int v2) {if (v1 < 0 || v2 < 0 || v1 >= numOfVexs || v2 >= numOfVexs)throw new ArrayIndexOutOfBoundsException();edges[v1][v2] = 0;edges[v2][v1] = 0;return true;}// 查找边public int getEdge(int v1,int v2){if (v1 < 0 || v2 < 0 || v1 >= numOfVexs || v2 >= numOfVexs)throw new ArrayIndexOutOfBoundsException();return edges[v1][v2];}// 深度优先搜索遍历public String depthFirstSearch(int v) {}// 广度优先搜索遍历public String breadFirstSearch(int v) {}// 实现Dijkstra算法public int[] dijkstra(int v) {}
}邻接表
前面的邻接矩阵方法实际上是图的一种静态存储方法。建立这种存储结构时需要预先知道图中顶点的个数。如果图结构本身需要在解决问题的过程中动态地产生,则每增加或者删除一个顶点都需要改变邻接矩阵的大小,显然这样做的效率很低。除此之外,邻接矩阵所占用的存储单元数目至于图中的顶点的个数有关,而与边或弧的数目无关,若图是一个稀疏图的话,必然造成存储空间的浪费。邻接表很好地解决了这些问题。
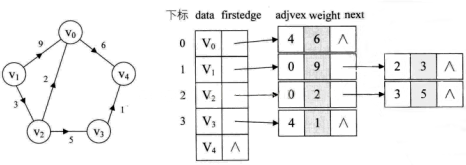
邻接表的存储方式是一种顺序存储与链式存储相结合的存储方式,顺序存储部分用来保存图中的顶点信息,链式存储部分用来保存图中边或弧的信息。具体的做法是,使用一个一维数组保存图中顶点的信息,数组中每个数组元素包含两个域。其存储结构如下:
| 域名称 | 域作用 |
| 顶点域(data) | 存放与顶点有关的信息 |
| 头指针域(firstadj) | 存放与该顶点相邻的所有顶点组成的单链表的头指针 |
邻接单链表中的每个结点表示依附于该结点的一条边,称作边结点,边结点的数据结构如下:
| 域名称 | 域作用 |
| 邻接点域(adjvex) | 指示与顶点的邻接点在图中的位置,对应着一维数组中的索引号 |
| 数据域(info) | 存储着边或弧的相关信息,如权值等 |
| 链域(nextadj) | 指向与顶点相邻的下一个边结点的指针 |
总而言之,邻接表是一个数组,数组的每个元素包含顶点信息和单链表的头指针两部分。而单链表的结构分成与顶点相邻的元素信息、边的信息和下一个与顶点相邻的元素指针。下面是图的邻接表Java代码实现:
public class GraphAdjList<E> implements IGraph<E> {// 邻接表中表对应的链表的顶点private static class ENode {int adjvex; // 邻接顶点序号int weight;// 存储边或弧相关的信息,如权值ENode nextadj; // 下一个邻接表结点public ENode(int adjvex, int weight) {this.adjvex = adjvex;this.weight = weight;}}// 邻接表中表的顶点private static class VNode<E> {E data; // 顶点信息ENode firstadj; // //邻接表的第1个结点};private VNode<E>[] vexs; // 顶点数组private int numOfVexs;// 顶点的实际数量private int maxNumOfVexs;// 顶点的最大数量private boolean[] visited;// 判断顶点是否被访问过@SuppressWarnings("unchecked")public GraphAdjList(int maxNumOfVexs) {this.maxNumOfVexs = maxNumOfVexs;vexs = (VNode<E>[]) Array.newInstance(VNode.class, maxNumOfVexs);}// 得到顶点的数目public int getNumOfVertex() {return numOfVexs;}// 插入顶点public boolean insertVex(E v) {if (numOfVexs >= maxNumOfVexs)return false;VNode<E> vex = new VNode<E>();vex.data = v;vexs[numOfVexs++] = vex;return true;}// 删除顶点public boolean deleteVex(E v) {for (int i = 0; i < numOfVexs; i++) {if (vexs[i].data.equals(v)) {for (int j = i; j < numOfVexs - 1; j++) {vexs[j] = vexs[j + 1];}vexs[numOfVexs - 1] = null;numOfVexs--;ENode current;ENode previous;for (int j = 0; j < numOfVexs; j++) {if (vexs[j].firstadj == null)continue;if (vexs[j].firstadj.adjvex == i) {vexs[j].firstadj = null;continue;}current = vexs[j].firstadj;while (current != null) {previous = current;current = current.nextadj;if (current != null && current.adjvex == i) {previous.nextadj = current.nextadj;break;}}}for (int j = 0; j < numOfVexs; j++) {current = vexs[j].firstadj;while (current != null) {if (current.adjvex > i)current.adjvex--;current = current.nextadj;}}return true;}}return false;}// 定位顶点的位置public int indexOfVex(E v) {for (int i = 0; i < numOfVexs; i++) {if (vexs[i].data.equals(v)) {return i;}}return -1;}// 定位指定位置的顶点public E valueOfVex(int v) {if (v < 0 || v >= numOfVexs)return null;return vexs[v].data;}// 插入边public boolean insertEdge(int v1, int v2, int weight) {if (v1 < 0 || v2 < 0 || v1 >= numOfVexs || v2 >= numOfVexs)throw new ArrayIndexOutOfBoundsException();ENode vex1 = new ENode(v2, weight);// 索引为index1的顶点没有邻接顶点if (vexs[v1].firstadj == null) {vexs[v1].firstadj = vex1;}// 索引为index1的顶点有邻接顶点else {vex1.nextadj = vexs[v1].firstadj;vexs[v1].firstadj = vex1;}ENode vex2 = new ENode(v1, weight);// 索引为index2的顶点没有邻接顶点if (vexs[v2].firstadj == null) {vexs[v2].firstadj = vex2;}// 索引为index1的顶点有邻接顶点else {vex2.nextadj = vexs[v2].firstadj;vexs[v2].firstadj = vex2;}return true;}// 删除边public boolean deleteEdge(int v1, int v2) {if (v1 < 0 || v2 < 0 || v1 >= numOfVexs || v2 >= numOfVexs)throw new ArrayIndexOutOfBoundsException();// 删除索引为index1的顶点与索引为index2的顶点之间的边ENode current = vexs[v1].firstadj;ENode previous = null;while (current != null && current.adjvex != v2) {previous = current;current = current.nextadj;}if (current != null)previous.nextadj = current.nextadj;// 删除索引为index2的顶点与索引为index1的顶点之间的边current = vexs[v2].firstadj;while (current != null && current.adjvex != v1) {previous = current;current = current.nextadj;}if (current != null)previous.nextadj = current.nextadj;return true;}// 得到边public int getEdge(int v1, int v2) {if (v1 < 0 || v2 < 0 || v1 >= numOfVexs || v2 >= numOfVexs)throw new ArrayIndexOutOfBoundsException();ENode current = vexs[v1].firstadj;while (current != null) {if (current.adjvex == v2) {return current.weight;}current = current.nextadj;}return 0;}// 深度优先搜索遍历public String depthFirstSearch(int v) {}// 广度优先搜索遍历public String breadFirstSearch(int v) {}// 实现Dijkstra算法public int[] dijkstra(int v) {}
}
其中关于图的几种遍历方式(深度优先、广度优先)和Dijkstra算法,在下一篇文章中会具体地讲到。