【二分·习题】Best Cow Fence（实数域上的二分答案）

Problem

题目描述
农场主 John (简称 FJ) 的农场有一长排的 N (1 <= N <= 100,000)块地组成. 每块地有一定数量 (ncows) 的牛, 1 <= ncows <=2000.

FJ 想修建环绕邻接的一组地块的栅栏, 以最大化这组地块中平均每块地中牛的个数.

这组地块必须包含至少 F (1 <= F <= N) 块地, F 作为输入给出.

给定约束, 计算出栅栏的布置情况以最大化平均数.

友情提示：由于本题过于陈旧，数据上有一些偏差，请在解答的时候精度设为"1e-5".

输入格式
第一行: 空格分隔的两个整数, N 和 F.

第2到第N+1行: 每行包含一个整数, 一块地中的牛数. 行 2 给出地块 1 中的牛数, 行 3 给出地块 2 中的牛数, …

输出格式
一行一个整数, 它是最大平均数的 1000 倍.

Solution

这道题的话是一个实数域上的二分答案，主要难点就是实数二分的书写以及如何求解最大平均数。

对于前者，只需要记住大致的一个模板即可。

while (l+eps<r)	{
    double mid=(l+r)/2;if (check(mid)) l=mid;else r=mid;}

其中输出的值l和r均可。eps是设置的精度，这里是$10^{?5}$

对于后者，也就是这里的check，我们可以这么思考：

• 对于一个平均数大于s的长度为len的序列，其总和$=len?s+k,k>0.$
• 对于一个平均数小于s的长度为len的序列，其总和$=len?s?k,k>0.$
• 对于一个平均数等于s的长度为len的序列，其总和$=len?s.$

因此我们只需要二分每一个平均数，只要哪个大于L的字段的平均数比L大，这就是一个合法的子段。

将所有数都减去这个平均数$s$，存在子段大于$0$就说明合法。

如何判断子段大于$0$呢？

以i结尾的字段中，最大的是：$sum[i]?min(sum[j]).$

j是不断更新的，在i更新的同事更新j即可在$O(n)$内完成$check$。

一些细节问题：

• 关于单调性：
  
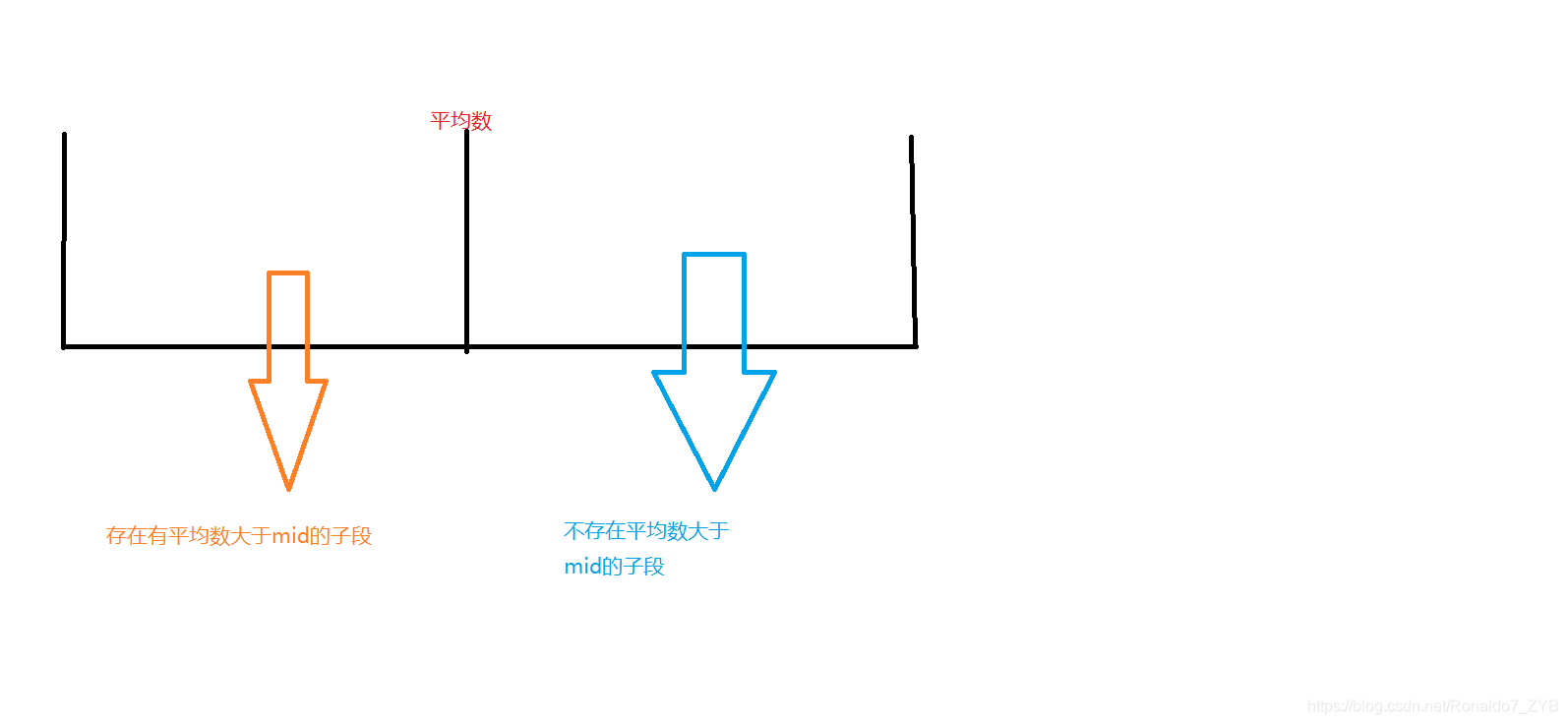
• 为什么要用实数：因为平均数。

代码如下：

#include<bits/stdc++.h>
using namespace std;
int n,f;
double mins,ans;
double b[200000];
double a[200000];
double sum[200000];
bool check(double s)
{
    ans=-1e9;mins=1e9;for (int i=1;i<=n;++i) b[i]=a[i]-s;for (int i=1;i<=n;++i) sum[i]=sum[i-1]+b[i];for (int i=f;i<=n;++i){
    mins=min(mins,sum[i-f]);ans=max(ans,sum[i]-mins);}return ans>=0;
}
int main(void)
{
    freopen("cowfnc.in","r",stdin);freopen("cowfnc.out","w",stdout);scanf("%d %d",&n,&f);for (int i=1;i<=n;++i)scanf("%lf",a+i);double l=-1e9,r=1e9,eps=1e-5;while (l+eps<r)	{
    double mid=(l+r)/2;if (check(mid)) l=mid;else r=mid;}cout<<int(r*1000)<<endl; return 0;
}