Encoder-Decoder和Seq2Seq with Attention

1 什么是 Encoder-Decoder ？

Encoder-Decoder 模型主要是 NLP 领域里的概念。它并不特值某种具体的算法，而是一类算法的统称。Encoder-Decoder 算是一个通用的框架，在这个框架下可以使用不同的算法来解决不同的任务,这个框架很好的诠释了机器学习的核心思路：将现实问题转化为数学问题，通过求解数学问题，从而解决现实问题。

Encoder 又称作编码器。它的作用就是「将现实问题转化为数学问题」

Decoder 又称作解码器，他的作用是「求解数学问题，并转化为现实世界的解决方案」

把 2 个环节连接起来，用通用的图来表达则是下面的样子：

< center> 图1

Encoder-Decoder框架可以这么直观地去理解_[1]：可以把它看作适合处理由一个句子（或篇章）生成另外一个句子（或篇章）的通用处理模型。对于句子对<X,Y>，我们的目标是给定输入句子X，期待通过Encoder-Decoder框架来生成目标句子Y。X和Y可以是同一种语言，也可以是两种不同的语言。而X和Y分别由各自的单词序列构成:
$$X=<x_1,x_2,...,x_m>$$$$Y=<y_1,y_2,...,y_n>$$

Encoder对输入句子X进行编码，将输入句子通过非线性变换转化为中间语义表示C：
$$C=F(x_1,x_2,...,x_m)$$对于解码器Decoder来说，其任务是根据句子X的中间语义表示C和之前已经生成的历史信息y1,y2….yi-1来生成i时刻要生成的单词$y_i$
$$y_i=g(C,y_1,y_2,...,y_n)$$每个$y_i$都依次这么产生，那么看起来就是整个系统根据输入句子X生成了目标句子Y。

因此，准确的说，Encoder-Decoder并不是一个具体的模型，而是一类框架。Encoder和Decoder部分可以是任意的文字，语音，图像，视频数据，模型可以采用CNN，RNN，BiRNN、LSTM、GRU等等。所以基于Encoder-Decoder，我们可以设计出各种各样的应用算法。

为了方便理解，我们先选取了编码和解码都是RNN的组合：
在RNN中，x={x1，x2，…，xt}代表输入，在每个时间步t，RNN的隐藏状态 $h_t$当前时刻隐层状态是由上一时刻的隐层状态和当前时刻的输入决定的，其更新公式如下：
$$h_t=f(h_{t?1},x)$$
其中，$h_t$就是一个大小为rnn_size的隐含状态

获得了各个时刻的隐层状态以后，再将信息汇总，生成最后的语义编码C（就是上图的向量C）
C=q({fh1,...,hTx})C=q({\{f_{h1},...,h_{T_x}\}})C=q({ fh1?,...,hTx??})
q表示某种非线性函数。在[1]中，作者采用LSTM网络作为Encoder网络，实际上在LSTM或者基本的RNN网络中，当前时刻计算完后是看不见前面时刻的隐层状态的了，所以就是用最后一个时刻的隐层状态作为语义编码C，即
$$C=h_{T_x}$$
解码过程我们要根据给定的语义编码C和已经生成的输出序列$y_1,y_2,\dots y_{t?1}$来预测下一个输出的单词yt，实际上就是把生成句子$y=y_1,y_2,\dots y_T$的联合概率分解成按顺序的条件概率：
p(y)=∏t=1Tp(yt∣{y1,y2,...yt?1},C)p(y)=\prod_{t=1}^{T}p(y_t|\{y_1,y_2,...y_{t-1}\},C)p(y)=t=1∏T?p(yt?∣{ y1?,y2?,...yt?1?},C)而每一个条件概率又可以写成:
p(yt∣{y1,y2,...yt?1},C)=g(yt?1,st,C)p(y_t|\{y_1,y_2,...y_{t-1}\},C)=g(y_{t-1},s_t,C)p(yt?∣{ y1?,y2?,...yt?1?},C)=g(yt?1?,st?,C)其中$s_t$是输出RNN中的隐藏层，C代表之前提过的语义向量，$y_{t?1}$表示上个时刻的输出。$g$表示一种非线性变换，往往就是指一种多层的函数，可以输出$y_t$的概率（比如多层RNN后接softmax）。

所以，在文本序列的Encoder-Decoder模型中，原本RNN（LSTM）语言模型是要估计$p(y1,y2,\dots yT|x1,x2,...,xT\prime )$，给定一串输入x，得到一串输出y（不需要等长），但是因为Encoder-Decoder中间用语义编码c把前后两部分隔开了，所以输出句子y只需要和c相关即可。

训练时只要端到端训练RNN（LSTM）网络就可以了，在每一个句子末尾打上一个end-of-sentence symbol， EOS符号，用输入句子来预测输出句子。这样的模型就可以完成基本的英语-法语的翻译任务。

关于 Encoder-Decoder，有2 点需要说明：

• 不论输入和输出的长度是什么，中间的「向量 c」 长度都是固定的（这也是它的缺陷，下文会详细说明）
• 根据不同的任务可以选择不同的编码器和解码器（可以是一个 RNN ，但通常是其变种 LSTM 或者 GRU ，刚已经提到了一些）

2 Attention Model（AM）

基本的Encoder-Decoder模型非常经典，但是也有局限性。最大的局限性就在于编码和解码之间的唯一联系就是一个固定长度的语义向量c。也就是说，编码器要将整个序列的信息压缩进一个固定长度的向量中去。但是这样做有两个弊端，一是语义向量无法完全表示整个序列的信息，还有就是先输入的内容携带的信息会被后输入的信息稀释掉，或者说，被覆盖了。输入序列越长，这个现象就越严重。这就使得在解码的时候一开始就没有获得输入序列足够的信息， 那么解码的准确度自然也就要打个折扣了[3]。

我们称上面这一现象为“注意力不集中”，为什么说它注意力不集中呢？请观察下目标句子Y中每个单词的生成过程如下：

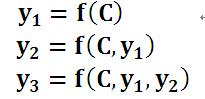
其中f是decoder的非线性变换函数。从这里可以看出，在生成目标句子的单词时，不论生成哪个单词，是y1,y2也好，还是y3也好，他们使用的句子X的语义编码C都是一样的，没有任何区别。
而语义编码C是由句子X的每个单词经过Encoder 编码产生的，这意味着不论是生成哪个单词，y1,y2还是y3，其实句子X中任意单词对生成某个目标单词yi来说影响力都是相同的，没有任何区别。

这就是为何说这个模型没有体现出注意力的缘由。这类似于你看一幅画，但是没有注意焦点一样。如果拿机器翻译来解释这个分心模型的Encoder-Decoder框架更好理解，比如输入的是英文句子：Tom chase Jerry，Encoder-Decoder框架逐步生成中文单词：“汤姆”，“追逐”，“杰瑞”。在翻译“杰瑞”这个中文单词的时候，分心模型里面的每个英文单词对于翻译目标单词“杰瑞”贡献是相同的，很明显这里不太合理，显然“Jerry”对于翻译成“杰瑞”更重要，但是分心模型是无法体现这一点的，这就是为何说它没有引入注意力的原因。

（其实如果Encoder是RNN的话，理论上越是后输入的单词影响越大，并非等权的，估计这也是为何Google提出Sequence to Sequence模型时发现把输入句子逆序输入做翻译效果会更好的小Trick的原因）。

没有引入注意力的模型在输入句子比较短的时候估计问题不大，但是如果输入句子比较长，此时所有语义完全通过一个中间语义向量来表示，单词自身的信息已经消失，可想而知会丢失很多细节信息，这也是为何要引入注意力模型的重要原因。

上面的例子中，如果引入AM模型的话，应该在翻译“杰瑞”的时候，体现出英文单词对于翻译当前中文单词不同的影响程度，比如给出类似下面一个概率分布值：

（Tom,0.3）(Chase,0.2)(Jerry,0.5)
以上每个英文单词的概率代表了翻译当前单词“杰瑞”时，注意力分配模型分配给不同英文单词的注意力大小。因为引入了新的信息，这对于正确翻译目标单词肯定是有帮助的。

同理，目标句子中的每个单词都应该学会其对应的源语句子中单词的注意力分配概率信息。这意味着在生成每个单词$Y_i$的时候，原先都是相同的中间语义表示C会替换成根据当前生成单词而不断变化的$C_i$。

图二

即生成目标句子单词的过程成了下面的形式：

而每个$C_i$可能对应着不同的源语句子单词的注意力分配概率分布，比如对于上面的英汉翻译来说，其对应的信息可能如下：

其中，f2函数代表Encoder对输入英文单词的某种变换函数，比如如果Encoder是用的RNN模型的话，这个f2函数的结果往往是某个时刻输入xi后隐层节点的状态值；
\ \ \ \ \ g代表Encoder根据单词的中间表示合成整个句子中间语义表示的变换函数，一般的做法中，g函数就是对构成元素加权求和，也就是常常在论文里看到的下列公式：
$$C_i=\sum _{j=1}^T{a}_{ij}{h}_j$$

假设$C_i$中那个$i$就是上面的“汤姆”，那么$T_x$就等于3，代表输入句子的长度，$h1=f(“Tom”)$，$h2=f(“Chase”)$,$h3=f(“Jerry”)$，对应的注意力模型权值$a_i$分别是0.6,0.2,0.2，所以$g$函数就是个加权求和函数。如果形象表示的话，翻译中文单词“汤姆”的时候，数学公式对应的中间语义表示$C_i$的形成过程类似下图：

图3

这里还有一个问题：生成目标句子某个单词，比如“汤姆”的时候，你怎么知道AM模型所需要的输入句子单词注意力分配概率分布值呢？就是说“汤姆”对应的概率分布：
（Tom,0.6）(Chase,0.2)(Jerry,0.2）
是如何得到的呢？

为了便于说明，我们假设对图1的非AM模型的Encoder-Decoder框架进行细化，Encoder采用RNN模型，Decoder也采用RNN模型，这是比较常见的一种模型配置，则图1的图转换为下图：

图4 RNN作为具体模型的Encoder-Decoder框架

那么用下图可以较为便捷地说明注意力分配概率分布值的通用计算过程：

图5 AM注意力分配概率计算

对于采用RNN的Decoder来说，如果要生成yi单词，在时刻$i$，我们是可以知道在生成$Y_i$之前的隐层节点i时刻的输出值$H_i$的，而我们的目的是要计算生成$Y_i$时的输入句子单词“Tom”、“Chase”、“Jerry”对$Y_i$的注意力分配概率分布$Pdf(\alpha )$
那么我们就可以用$i$时刻的隐层节点状态$H_i$,去和输入句子中每个单词对应的RNN隐层节点状态$h_j$进行对比——即通过函数$F(h_j,H_i)$来获得目标单词$Y_i$和每个输入单词对应的对齐可能性，(这个$F$函数在不同论文里可能会采取不同的方法)，然后函数$F$的输出经过Softmax进行归一化就得到了符合概率分布取值区间的注意力分配概率分布数值。

2.1 AM Decoder解码

使用了attention模型的解码部分的条件概率写作
$$p(y_i|y_1,\dots ,y_{i?1},X)=g(y_{i?1},s_i,c_i)$$上式$S_i$表示解码器i时刻的隐藏状态。计算公式是
$$s_i=f(s_{i?1},y_{i?1},c_i)$$注意这里的条件概率与每个目标输出$y_i$相对应的内容向量$C_i$有关。$C_i$的计算公式就是上文介绍的加权求和公式。
若考虑使用双向RNN的编码器，则可以认为$h_i$中包含了输入序列中第i个词以及前后一些词的信息。将隐藏向量序列按权重相加，表示在生成第j个输出的时候的注意力分配是不同的。下面就要根据第$i?1$个输出隐藏状态$s_{i?1}$和输入中各个隐藏状态来计算注意力分布：

写成公式：
$$a_{ij}=\frac{exp(e_{ij})}{{\sum }_{k?1}^{T_x}exp(e_{ik})}$$ $$e_{ij}=a(s_{i?1},h_j)$$
$\alpha$是权值矩阵，a是一种对齐方式(alignment model)
也就是说，$s_{i?1}$先跟每个$h$分别计算得到一个数值，然后使用softmax得到i时刻的输出在$T_x$个输入隐藏状态中的注意力分配向量。这个分配向量也就是计算$C_i$的权重。

我们现在再把公式按照执行顺序汇总一下：
$$\begin{array}{rl}& e_{ij}=a(s_{i?1},h_j)\\ & {\alpha }_{ij}=\frac{exp(e_{ij})}{{\sum }_{k=1}^{T_x}exp(e_{ik})}\\ & c_i=\sum _{j=1}^{T_x}{\alpha }_{ij}{h}_j\\ & s_i=f(s_{i?1},y_{i?1},c_i)\\ & y_i=g(y_{i?1},s_i,c_i)\end{array}$$

2.2 Encoder 编码

考虑一个具体完整的输入-输出流的模型：

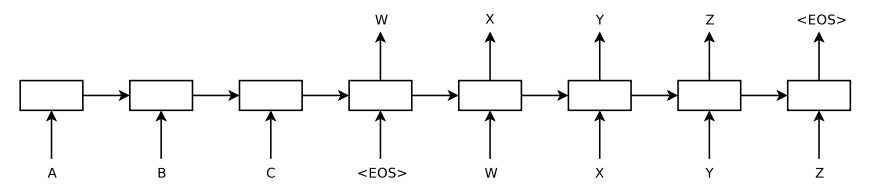
ABC为encoder的输入，WXYZ为decoder的输入。encoder会将最后得到的隐藏层的状态$h_t$输入到decoder的第一个cell里。因此从整体上看，从输入到输出像是一条“线性的数据流”。
具体来说，encoder的过程如下图。

对应decoder阶段：

得到了encoder represention，即encoder的最后一个时间步长的隐层ht以后，输入到decoder的第一个cell里，然后通过一个激活函数和softmax层，得到候选的symbols，筛选出概率最大的symbol，然后作为下一个时间步长的输入，传到cell中。这样，我们就得到了我们的目标p(y)=∏t=1Tp(yt∣{y1,y2,...yt?1},C)p(y)=\prod_{t=1}^{T}p(y_t|\{y_1,y_2,...y_{t-1}\},C)p(y)=∏t=1T?p(yt?∣{ y1?,y2?,...yt?1?},C)

2.3 AM Encoder 编码举例

在论文NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE 中，Seq2Seq With Attention时，作者处理Encoders是通过双向RNN简单进行了处理（并不像上面处理Decoder那样引入了权重）
用示意图表示：

上图中，encoder和decoder都发生了变化。对于encoder，使用了双向RNN，因为希望不仅能得到前向的词的顺序，还希望能够得到反向的词的顺序。使用$\overrightarrow{h_j}$代表$h_j$前向的隐层状态，使用$\overleftarrow{h_j}$代表$h_j$的反向隐层状态，$h_j$的最终状态为将两者连接（concat）起来，即$$hj=[\overrightarrow{h_j};\overleftarrow{h_j}]$$

这样处理，原因是传统的单向的RNN中，数据是按顺序输入的，因此第j个隐藏状态${\overrightarrow{h}}_j$只能携带第j个单词本身以及之前的一些信息；而如果逆序输入，则$\overleftarrow{h_j}$包含第j个单词及之后的一些信息。如果把这两个结合起来，$hj=[\overrightarrow{h_j};\overleftarrow{h_j}]$就包含了第j个输入和前后的信息。

[1]https://blog.csdn.net/malefactor/article/details/50550211
[2]https://www.cnblogs.com/sxron/articles/7039699.html
[3]https://blog.csdn.net/u014595019/article/details/52826423
[4]https://arxiv.org/pdf/1409.0473.pdf