在统计和数据挖掘中，亲和传播（AP）是基于数据点之间"消息传递"概念的聚类算法。与诸如k-means或k-medoids的聚类算法不同，亲和传播不需要在运行算法之前确定或估计聚类的数量。 类似于k-medoids，亲和力传播算法发现"样本"，输入集合的成员，输出聚类结果。
一 算法描述
2.1基本介绍
我们让(x1,…xn)作为一系列的数据点，然后用矩阵S代表各个数据点之间的相似度，一般相似度的判断有欧氏距离，马氏距离，汉明距离。如果S（i,k）>S(i,j)则表示i到k的距离比i到j的距离近。其中S(k,k)表示节点k作为k的聚类中心的合适程度，可以理解为，节点k成为聚类中心合适度，在最开始时，这个值是初始化的时候使用者给定的值，会影响到最后聚类的数量。
这个算法通过迭代两个消息传递步骤来进行，以更新下面两个矩阵：
代表(Responsibility)矩阵R：r(i,k)表示第k个样本适合作为第i个样本的类代表点的代表程度。说白了K为男人，i为女人，代表矩阵R表示，这个男人成为i这个女人老公的适合程度。
适选(Availabilities)矩阵A=[a(i,k)]N×N：a(i,k)表示第i个样本选择第k个样本作为类代表样本的适合程度，同理表示i选择K作为自己老公的可能性。当然，这个社会是相对于封建社会有点进步的，比如也会征求女方的意见，但是又有一定弊端，这个男人K可以三妻四妾。所以K这个聚类中心，周围可以有许多样本i。所以有的人叫R矩阵为吸引度矩阵，矩阵A为归属度矩阵也是不无道理的。
2.2 算法的迭代公式
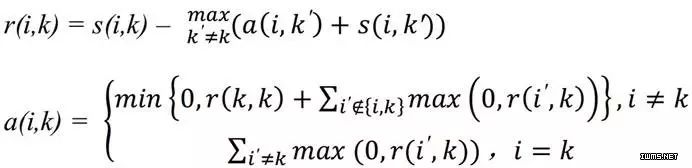
对于代表矩阵r：
假设现在有一个聚类中心K，我们找到另外一个假想的聚类中心k'，重新定义K'的代表矩阵和适合矩阵：
，找出这两个值相加最大的那一个，在用我们的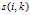
减去这个最大的，就表示这个K的聚类中心对i这个样本的吸引程度。你想想，最大情敌的吸引力都没有我高，那我岂不是最牛叉？？？
对于适合矩阵a：
我们要明白一个道理，如果一个男人对大部分女人的吸引力都很大，那么这个男人对你这个女人的吸引力的可能性是不是比别人大一点？明白了这个道理。同理如果节点k作为其他节点i'的聚类中心的合适度很大，那么节点k作为节点i的聚类中心的合适度也可能会较大，由此就可以先计算节点k对其他节点的吸引度，r(i',k)，然后做一个累加和表示节点k对其他节点的吸引度，得到：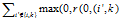
。等等r(k,k)是什么意思呢，一般帅的人是不是都是特别容易自恋？你懂得，所以这个表示样本选择自己作为聚类中心的自恋程度。为了不让这个值过大，影响整体结果，将这个值控制在0以下。当i=k的时候我们选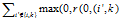就可以了。a(k,k)表示K这个作为聚类中心的能力。
注意有时候为了防止参数更新时的震动需要引入一个减震参数damping。Damping计算如下：
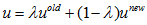
二 算法实现
function idx = AP(S)
N = size(s,1);
A=zeros(N,N);
R=zeros(N,N); % Initialize messages
lam=0.9; % Set damping factor
same_time = -1;
for iter=1:10000
% Compute responsibilities
Rold=R;
AS=A+S;
[Y,I]=max(AS,[],2);
for i=1:N
AS(i,I(i))=-1000;
end
[Y2,I2]=max(AS,[],2);
R=S-repmat(Y,[1,N]);
for i=1:N
R(i,I(i))=S(i,I(i))-Y2(i);
end
R=(1-lam)*R+lam*Rold; % Dampen responsibilities
% Compute availabilities
Aold=A;
Rp=max(R,0);
for k=1:N
Rp(k,k)=R(k,k);
end
A=repmat(sum(Rp,1),[N,1])-Rp;
dA=diag(A);
A=min(A,0);
for k=1:N
A(k,k)=dA(k);
end;
A=(1-lam)*A+lam*Aold; % Dampen availabilities
if(same_time == -1)
E=R+A;
[tt idx_old] = max(E,[],2);
same_time = 0;
else
E=R+A;
[tt idx] = max(E,[],2);
if(sum(abs(idx_old-idx)) == 0)
same_time = same_time + 1;
if(same_time == 10)
iter
break;
end
end
idx_old = idx;
end
end
E=R+A;
[tt idx] = max(E,[],2);
% figure;
% for i=unique(idx)'
% ii=find(idx==i);
% h=plot(x(ii),y(ii),'o');
% hold on;
% col=rand(1,3);
% set(h,'Color',col,'MarkerFaceColor',col);
% xi1=x(i)*ones(size(ii)); xi2=y(i)*ones(size(ii));
% line([x(ii)',xi1]',[y(ii)',xi2]','Color',col);
% end;
总结：算法讲解部分到这里结束了。谢谢大家，能否走一波关注？哈哈
