题目传送门
Description
司令部的将军们打算在N * M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成,地图的每一格可能是山地(用"H" 表示),也可能是平原(用"P"表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
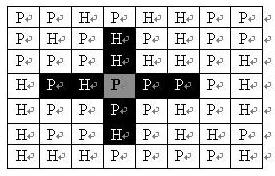
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
Input
第一行包含两个由空格分割开的正整数,分别表示N和M;
接下来的N行,每一行含有连续的M个字符(‘P’或者’H’),中间没有空格。按顺序表示地图中每一行的数据。N <= 100;M <= 10。
Output
仅一行,包含一个整数K,表示最多能摆放的炮兵部队的数量。
Sample Input
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
Sample Output
6
题解
- 首先根据数据范围很容易看出来是状压DP
- 这道题和 玉米田 这道题很像(点击链接查看原题 & 题解)
- 由于炮弹的范围是 2,所以枚举上两行的状态,dp数组也需要增加一维。
- 定义: DP【i】【j】【k】:第 i 行状态为 j 时,上一行状态为 k 时的最多部队数量
- 平原:1;山地:0
- 同样,需要预处理一下:在输入的时候,将每一行的状态转换成十进制存起来,并且需要记录在一行内,满足条件(任意两支部队不会横着打到对方)的状态。但是需要注意,按照题目的范围,这里是 1 << 10,直接开dp数组会MLE,实际上由于攻击距离是2,所以只有不到60种情况.
- 由于本题求的是最大的部队数量,所以在预处理的时候顺便求一下每个状态下 1(平原) 的数量
- 状态转移方程:dp[ 第i行 ][ 状态为j ][ 上一行状态为k ] = max(dp[i][j][k], dp[ 上一行:i-1 ][ 状态为k ][ 上上一行状态为t ] + 状态 j 的 1(平原) 的数量);
- 记得枚举每行的状态时,判断是否为输入允许的子集,并且上行下行是否冲突
- 最后跑一边取最大值即可
注意
- 还算是中规中矩的状压DP,挺简单的
- 记得空间只需要60即可,不然会 MLE
- 对第一行初始化的时候要考虑是否是输入的子集
外提供数据
1 1
P
1 1
H
12 9
HPHHPHHPH
PPPHHPPHP
HHPHHHHPP
PHHHHPHHP
HHHPHPHHH
HPHPPPPPP
PPPHHPPPP
HPHPHHHPH
PPHPPPHPH
PHPHPPPHP
HPHHPHHPH
HPPPHHPHH
1
0
25
AC-Code
#include <bits/stdc++.h>using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);const int mod = 1e9;int f[101];
int dp[101][70][70]; // 第 i 行,状态为 j,i-1行状态为 k 时候的最大价值
int state[70];
int num[70]; // 每种状态 1 的个数
int cnt;
int main() {
ios;int n, m;while (cin >> n >> m) {
cnt = 0;memset(dp, 0, sizeof(dp));for (int i = 0; i < 1 << m; ++i) {
if (!(i & i << 2) && !(i & i << 1))state[cnt] = i;elsecontinue;int j = 0;int temp = i;for (j = 0; temp; ++j)temp &= (temp - 1); // 去掉最低位的 1num[cnt++] = j;}for (int i = 1; i <= n; ++i) {
string str;cin >> str;int sum = 0;for (int j = 0; j < m; ++j) {
if (str[j] == 'P') // 1 :平原, 0 :山sum = sum << 1 | 1;elsesum = sum << 1;}f[i] = sum;}for (int i = 0; i < cnt; i++) {
if (!(state[i] & f[1])) continue;dp[1][i][0] = num[i]; // 第 1 行初始化}for (int i = 2; i <= n; ++i) {
// 第 i 行for (int j = 0; j < cnt; ++j) {
// 枚举当前行状态 jif ((state[j] & f[i]) == state[j]) {
for (int k = 0; k < cnt; ++k) {
// 枚举上一行状态if ((state[k] & f[i - 1]) == state[k] && !(state[j] & state[k]))for (int t = 0; t < cnt; ++t) {
if ((state[t] & f[i - 2]) == state[t] && !(state[j] & state[t]) && !(state[k] & state[t]))dp[i][j][k] = max(dp[i][j][k], dp[i - 1][k][t] + num[j]);}}}}}int ans = 0;for (int i = 0; i < cnt; ++i) {
for (int j = 0; j < cnt; ++j) {
ans = max(ans, dp[n][i][j]);}}cout << ans << endl;}
}