前言
normalization方法已经广泛应用在深度模型中,并且发挥着重要作用,本文是对normalization方法的一些总结。
normalization
以神经网络中一个普通神经元为例,输入向量:
x = ( x 1 , x 2 , ? , x n ) (1) x = (x_1,x_2,\cdots,x_n) \tag{1} x=(x1?,x2?,?,xn?)(1)
通过运算后的输出为:
h = f ( x ) (2) h = f(x) \tag{2} h=f(x)(2)
实际情况下,x的分布可能相差很大,并不符合独立同分布的假设,normalization的基本思想就是:在对x进行运算之前,先进行平移和伸缩变换操作,使x的分布规范化成某个固定区间的标准分布,即:
h = f ( γ ? x ? μ σ + β ) (3) h = f(\gamma \cdot \frac{x - \mu}{\sigma} + \beta) \tag{3} h=f(γ?σx?μ?+β)(3)
其中, μ \mu μ 为平移参数(shift parameter), σ \sigma σ 为缩放参数(scale parameter),通过这两个参数进行平移和缩放变换,可以使输入x符合均值为0、方差为1的标准分布;之后, γ \gamma γ 为再缩放参数(re-scale parameter), β \beta β 为再平移参数(re-shift parameter),将数据最终变换为均值为 β \beta β ,方差为 γ \gamma γ 的分布。
normalization参数学习,对损失函数 l l l 使用链式法则:
对 x ^ i \hat{x}_i x^i? 有:
? l ? x ^ i = ? l ? y i ? γ (4) \frac{\partial l}{\partial \hat{x}_i} = \frac{\partial l}{\partial y_i} \cdot \gamma \tag{4} ?x^i??l?=?yi??l??γ(4)
对 σ 2 \sigma^2 σ2 有:
? l ? σ 2 = ∑ i = 1 m ? l ? x ^ i ? ( x i ? μ ) ? ? 1 2 ( σ 2 + ? ) ? 3 2 (5) \frac{\partial l}{\partial \sigma^2} = \sum_{i=1}^{m} \frac{\partial l}{\partial \hat{x}_i} \cdot (x_i - \mu) \cdot \frac{-1}{2} (\sigma^2 + \epsilon)^{-\frac{3}{2}} \tag{5} ?σ2?l?=i=1∑m??x^i??l??(xi??μ)?2?1?(σ2+?)?23?(5)
对 μ \mu μ 有:
? l ? μ = ∑ i = 1 m ? l ? x ^ i ? ? 1 σ 2 + ? (6) \frac{\partial l}{\partial \mu} = \sum_{i=1}^{m} \frac{\partial l}{\partial \hat{x}_i} \cdot \frac{-1}{\sqrt{\sigma^2 + \epsilon}} \tag{6} ?μ?l?=i=1∑m??x^i??l??σ2+???1?(6)
对 x i x_i xi? 有:
? l ? x i = ? l ? x ^ i ? 1 σ 2 + ? + ? l ? σ 2 ? 2 ( x i ? μ ) m + ? l ? μ ? 1 m (7) \frac{\partial l}{\partial x_i} = \frac{\partial l}{\partial \hat{x}_i} \cdot \frac{1}{\sqrt{\sigma^2 + \epsilon}} + \frac{\partial l}{\partial \sigma^2} \cdot \frac{2(x_i - \mu)}{m} + \frac{\partial l}{\partial \mu} \cdot \frac{1}{m} \tag{7} ?xi??l?=?x^i??l??σ2+??1?+?σ2?l??m2(xi??μ)?+?μ?l??m1?(7)
对 γ \gamma γ 有:
? l ? γ = ∑ i = 1 m ? l ? y i ? x ^ i (8) \frac{\partial l}{\partial \gamma} = \sum_{i=1}^{m} \frac{\partial l}{\partial y_i} \cdot \hat{x}_i \tag{8} ?γ?l?=i=1∑m??yi??l??x^i?(8)
对 β \beta β 有:
? l ? β = ∑ i = 1 m ? l ? y i (9) \frac{\partial l}{\partial \beta} = \sum_{i=1}^{m} \frac{\partial l}{\partial y_i} \tag{9} ?β?l?=i=1∑m??yi??l?(9)
batch normalization
batch normalization,纵向规范化,针对单个神经元进行,利用网络训练时每个batch的数据来计算该神经元 x i x_i xi? 的均值和方差,从而实现对数据的规范化处理。
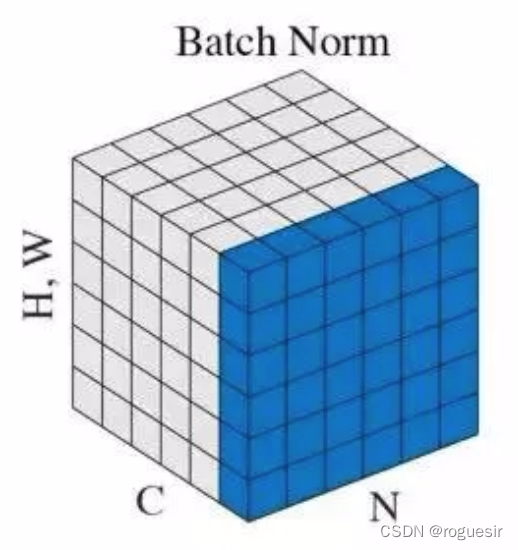
计算batch的均值:
μ = 1 m ∑ i = 1 m x i (10) \mu = \frac{1}{m} \sum_{i=1}^{m}x_i \tag{10} μ=m1?i=1∑m?xi?(10)
计算batch的方差:
σ 2 = 1 m ∑ i = 1 m ( x i ? μ ) 2 (11) \sigma^2 = \frac{1}{m}\sum_{i=1}^{m}(x_i-\mu)^2 \tag{11} σ2=m1?i=1∑m?(xi??μ)2(11)
对输入数据进行规范化处理,使其转变为均值为0,方差为1的标准分布:
x ^ i = x i ? μ σ 2 + ? (12) \hat{x}_i = \frac{x_i-\mu}{\sqrt{\sigma^2 + \epsilon}} \tag{12} x^i?=σ2+??xi??μ?(12)
再对数据进行再平移和再缩放操作,使数据分布限制在一定范围内:
y i = γ x ^ i + β (13) y_i = \gamma \hat{x}_i + \beta \tag{13} yi?=γx^i?+β(13)
BN的参数是一个batch下的均值和方差统计,这就要求每个batch的分布和整体数据近似同分布。如果batch之间的数据分布差异较小,可以看作是规范化过程中数据引入了微小噪声,可以增加模型的泛化能力,提高模型的鲁棒性;但如果batch之间的数据分布差异较大,则经过BN之后,映射的规范化空间也是不同的,就会增加模型的训练难度。
因此,在使用BN时,需要注意以下几点:首先,batch size不能太小,batch size太小会导致均值和方差的波动变大;其次,数据需进行随机的shuffle操作,避免相似数据在同一个batch中而出现分布差异大的情况。
需要注意的是,由于在训练阶段,BN每次只需要计算每个batch的均值和方差,而在线上预测阶段,请求的数据是单条的,因此模型在训练时会记录每个batch计算的结果进行指数移动平均后,作为线上预测的均值和方差。
在原论文中给出的BN有效的解释是:BN可以防止内部协方差转移,通过神经元加权计算后使用BN可以将数据的分布控制在一定波动范围内。后来MIT论文验证该解释是错的,BN的作用在于平滑了损失曲面,使得模型训练时可以更快速收敛,使用较大的学习率也不会出问题(BN在每一个batch中都会计算均值和方差,实际上是增加了模型的计算量,本应该增加模型的训练时长,但由于BN会使模型更快的收敛,少走弯路,实际上会减少模型的训练时间)。
此外,由于BN是对每个神经元的纵向规范化操作,对于推荐系统、图像问题,都具有很好的效果,但在NLP领域使用BN的效果并不理想,在NLP中主要使用layer normalization,下面进行介绍。
layer normalization
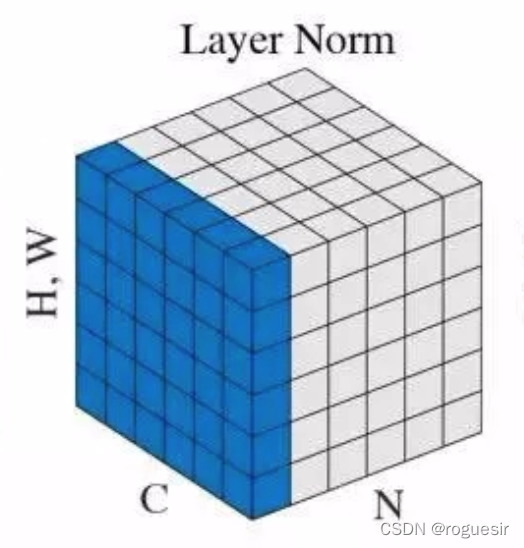
相比于BN,LN广泛使用于NLP模型中,是一种横向的规范化操作。LN会考虑这一层所有维度的输入,横向计算该层的均值和方差,然后对这一层的所有数据进行规范化操作。具体计算如下:
μ = 1 H ∑ i = 1 H x i σ = 1 H ∑ i = 1 H ( x i ? μ ) 2 (14) \mu = \frac{1}{H} \sum_{i=1}^{H} x_i \ \ \ \ \ \ \sigma = \sqrt{\frac{1}{H} \sum_{i=1}^{H} (x_i - \mu)^2} \tag{14} μ=H1?i=1∑H?xi? σ=H1?i=1∑H?(xi??μ)2?(14)
其中, H H H 为该层中隐层节点数量, μ \mu μ 为该层的均值, σ \sigma σ 为该层的方差。归一化的值为:
x ^ = x ? μ σ 2 + ? (15) \hat{x} = \frac{x - \mu}{\sqrt{\sigma ^2 + \epsilon}} \tag{15} x^=σ2+??x?μ?(15)
最后根据式(13)即为规范化结果。
上面也有提到,BN在推荐系统、图像上面的效果都很好,但在NLP模型中表现很差,其实归根结底还是数据本身的差异。在推荐系统中,每一维索引表示某个特征值或是特征值的高阶映射;在图像上,每一维索引表示某个像素点或是像素点的高阶映射,这两者都是实际存在的,并且描述的意义相同或近似。而在NLP领域,每一维是一个单词的映射,这个映射是人为构造的,并且由于语句长短不一,产出的向量长度也不一,这时候去纵向的考虑每个单词的信息提取,不如横向的考虑每个句子的整体信息,举个简单的例子:『今天 天气 很 好』和『我 在 写 博客』这两个句子,如果按照BN的逻辑,就应该是『今天』和『我』进行标准化,这显然不合理。
另外,LN操作仅仅是在一层神经元的输入,不需要考虑batch维度,因此也就不需要存储均值和方差,节省了额外的存储空间。
instance normalization
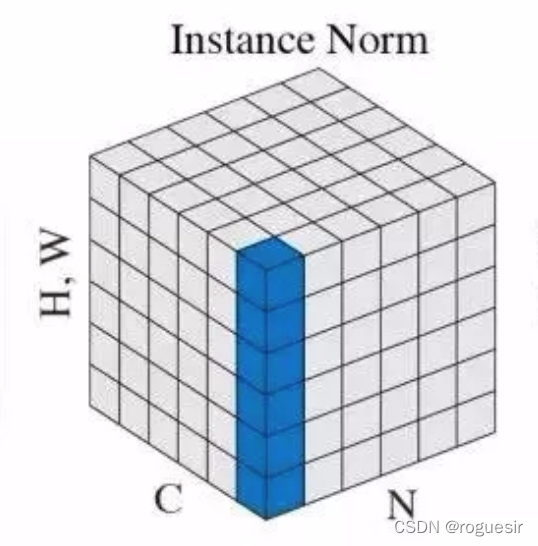
Instance Norm的计算逻辑如下:
μ t i = 1 H W ∑ l = 1 W ∑ m = 1 H x t i l m σ t i 2 = 1 H W ∑ l = 1 W ∑ m = 1 H ( x t i l m ? μ t i ) 2 (16) \mu_{ti} = \frac{1}{HW} \sum_{l=1}^{W} \sum_{m=1}^{H} x_{tilm} \ \ \ \ \ \ \sigma_{ti}^2 = \frac{1}{HW} \sum_{l=1}^{W} \sum_{m=1}^{H} (x_{tilm} - \mu_{ti})^2 \tag{16} μti?=HW1?l=1∑W?m=1∑H?xtilm? σti2?=HW1?l=1∑W?m=1∑H?(xtilm??μti?)2(16)
Instance Norm规范化:
x ^ t i l m = x t i l m ? μ t i σ t i 2 + ? (17) \hat{x}_{tilm} = \frac{x_{tilm} - \mu_{ti}}{\sqrt{\sigma_{ti}^2 + \epsilon}} \tag{17} x^tilm?=σti2?+??xtilm??μti??(17)
最后根据式(13)即为规范化结果。
group normalization
group normalization介于layer normalization和instance normalization之间,计算式需要定义超参数G,为group的数量
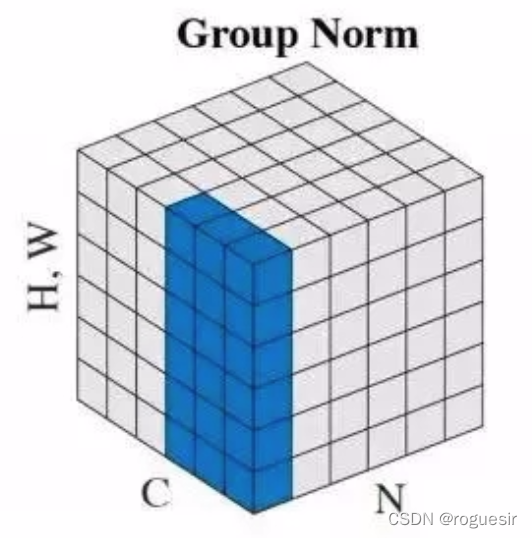
weighted normalization
回到神经元计算的基本逻辑上:
f ( x ) = W ? x + b (18) f(x)=W \cdot x + b \tag{18} f(x)=W?x+b(18)
上面介绍的各种标准化,实际上都是对输入 x x x 进行变换,而本节中的WN,则是对 W W W 进行规范化。具体方案是:将权重向量 W W W 分解为方向向量 v ^ \hat{v} v^ 和 向量模 g g g 。
f w ( x ) = W N ( W x ) = g ? v ^ ? x = g ? v ∣ ∣ v ∣ ∣ ? x = v ? g ? x ∣ ∣ v ∣ ∣ = f v ( g ? x ∣ ∣ v ∣ ∣ ) (19) \begin{aligned} f_w(x) &= WN(Wx)\\ &= g \cdot \hat{v} \cdot x \\ &= g \cdot \frac{v}{||v||} \cdot x \\ &= v \cdot g \cdot \frac{x}{||v||} \\ &= f_v (g \cdot \frac{x}{||v||}) \end{aligned} \tag{19} fw?(x)?=WN(Wx)=g?v^?x=g?∣∣v∣∣v??x=v?g?∣∣v∣∣x?=fv?(g?∣∣v∣∣x?)?(19)
对比式(3)可知,只需令: μ = 0 , σ = ∣ ∣ v ∣ ∣ , b = 0 \mu = 0 \ , \sigma = ||v|| \ , b=0 μ=0 ,σ=∣∣v∣∣ ,b=0 即可。
cosin normalization
还是回到神经元的基本变换,式(18)上, W W W 和 x x x 两个向量计算点积作为神经元的输出,点积是无界的,本质上也是计算两个向量的相似度,于是使用余弦相似度替代点积,这样还有一个好处,余弦相似度是有界的。
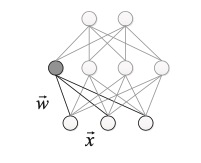
f w ( x ) = c o s θ = w ? x ∣ ∣ w ∣ ∣ ? ∣ ∣ x ∣ ∣ (20) f_w(x) = cos \theta = \frac{w \cdot x}{||w|| \cdot ||x||} \tag{20} fw?(x)=cosθ=∣∣w∣∣?∣∣x∣∣w?x?(20)
n e t n o r m = ( w ? μ w ) ? ( x ? μ x ) ∣ w ? μ w ∣ ∣ x ? μ x ∣ (21) net_{norm} = \frac{(w - \mu_w) \cdot (x - \mu_x)}{|w - \mu_w| |x - \mu_x |} \tag{21} netnorm?=∣w?μw?∣∣x?μx?∣(w?μw?)?(x?μx?)?(21)
其中, μ w \mu_w μw? 为向量 w w w 的均值, μ x \mu_x μx? 为向量 x x x 的均值
因为,
∣ w ? μ w ∣ = ∑ i ( w i ? μ w ) 2 (22) |w - \mu_w| = \sqrt{\sum_i (w_i - \mu_w)^2} \tag{22} ∣w?μw?∣=i∑?(wi??μw?)2?(22) ∣ x ? μ x ∣ = ∑ i ( x i ? μ x ) 2 (23) |x - \mu_x| = \sqrt{\sum_i (x_i - \mu_x)^2} \tag{23} ∣x?μx?∣=i∑?(xi??μx?)2?(23) σ w = 1 n ∑ i ( w i ? μ w ) 2 (24) \sigma_w = \sqrt{\frac{1}{n} \sum_i (w_i - \mu_w)^2} \tag{24} σw?=n1?i∑?(wi??μw?)2?(24) σ x = 1 n ∑ i ( x i ? μ x ) 2 (25) \sigma_x = \sqrt{\frac{1}{n} \sum_i (x_i - \mu_x)^2} \tag{25} σx?=n1?i∑?(xi??μx?)2?(25)
于是,cosine normalization转化为:
n e t n o r m = ( w ? μ w ) ? ( x ? μ x ) n σ w σ x (26) net_{norm} = \frac{(w - \mu_w) \cdot (x - \mu_x)}{ n \sigma_w \sigma_x} \tag{26} netnorm?=nσw?σx?(w?μw?)?(x?μx?)?(26)