0 - 写在前面
本系列共四篇,为林轩田机器学习基础篇学习笔记。主要内容可以总结概括为:线性模型通过非线性的变换可以得到非线性的模型,增强了模型对数据的拟合能力,但这样导致了在机器学习领域中一个很常见的问题,过拟合。为了解决这个问题引入了正则化因子(规则化因子)。而为了解决正则化因子的选择,模型的选择以及超参数的选择等问题引入了 validation v a l i d a t i o n 的相关方法。
- 机器学习笔记- Nonlinear Transformation N o n l i n e a r T r a n s f o r m a t i o n
- 机器学习笔记- Hazard of Overfitting H a z a r d o f O v e r f i t t i n g
- 机器学习笔记- Regularization R e g u l a r i z a t i o n
- 机器学习笔记- Validation V a l i d a t i o n
1 - Quadratic Hypothesis
之前介绍的模型是线性的,将所有的特征做一个加权和。现在我们要将这些 model m o d e l 延伸成更复杂的方法, 使用非线性的方式来做数据的分类。
线性分类器:模型是参数的线性函数,并且存在线性分类面,那么就是线性分类器。
logistic regression l o g i s t i c r e g r e s s i o n 属于线性模型还是非线性模型?
属于线性模型,因为 logistic regression l o g i s t i c r e g r e s s i o n 的决策边界是线性的。证明如下:
–知乎
或者可以简单的理解为逻辑斯蒂回归是将普通的线性模型的结果映射到一个(0, 1)的区间,然后划分一个界限(0.5)。
–知乎
线性模型的复杂度是受到控制的,这是线性模型的好处之一, 因为这样可以确保 Ein E i n (训练集误差)和 Eout E o u t (测试集误差)不会相差太远。但是缺点就是对于如下左图中的样本点,任一个线性分类器都无法完美的划分 × × 和 ? ? 。怎么突破线性模型的这个限制呢?也就是说,我们不再限制在使用“线”的方式,而是拓展一下使用其他的方式来解决这个二分类问题?
直观上来看, 如下的数据虽然不是线性可分的,但是是“圆圈”可分的。也就是说当使用函数: hsep(x)=sign(?x21?x22+0.6) h s e p ( x ) = s i g n ( ? x 1 2 ? x 2 2 + 0.6 ) 时可以正确的划分 × × 和 ? ? 。这个函数是一个以原点为中心 r2=0.6 r 2 = 0.6 的圆。
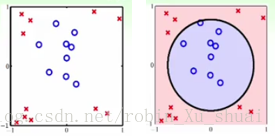
本节的目的是探讨如何系统化的设计算法使得原来的线性模型可以用于非线性可分的数据的分类。因为我们之前已经学到了一些针对分类的方法,例如 PLA P L A 算法, pocket p o c k e t 算法, linear regression l i n e a r r e g r e s s i o n 算法, logistic regression l o g i s t i c r e g r e s s i o n 算法,如何可以不更改这些算法本身而能应用于非线性可分的数据是我们关心的问题。
面对上图这样的数据,我们怎么可以得到一个“圆”形,而不再是一条线状的分类器呢?
对上面我们得到的分类函数 hsep(x) h s e p ( x ) 进行一些变量的重新定义和命名:
经过这样简单的重新命名我们发现线性的模型的形式又出现了,这样的“重命名”的过程其实是我们将所有的 X X 空间中的点通过多项式转换 映射到了一个新的空间中, 我们称之为 Z Z 空间。其中
而式子(1)告诉我们在 Z Z 空间中可以通过线性的模型
正确的划分 × × 和 ? ? 。线性模型我们在之前学过,这样我们面对的问题就变成了 Z Z 空间中可用线性模型解决的问题,只不过变量多了一点而已。
在得到了和
相关的一个线性分类器之后,再对应到 X X 空间,就得到了一个可以正确的划分
和 ? ? 的圆形的分类边界。这样我们就可以使用一个“圆”而不再是一条“线”对数据分类, 并且这个“圆”是使用线性模型做到的。

上述的那个重命名的过程,即数据从 X X 空间到 空间的过程称为特征转换( feature transform f e a t u r e t r a n s f o r m )。所以当经过这样的转换之后我们就可以在 Z Z 空间中使用我们熟悉的线性模型 , pocket p o c k e t , linear regression l i n e a r r e g r e s s i o n , logistic regression l o g i s t i c r e g r e s s i o n 来对数据进行分类。
(z0,z1,z2)=z=Φ(x)=(1,x21,x22) ( z 0 , z 1 , z 2 ) = z = Φ ( x ) = ( 1 , x 1 2 , x 2 2 )
h(x)=h~(z)=sign(w~TΦ(x))=sign(w0~+w1~x21+w0~x22) h ( x ) = h ~ ( z ) = s i g n ( w ~ T Φ ( x ) ) = s i g n ( w 0 ~ + w 1 ~ x 1 2 + w 0 ~ x 2 2 )
如果在 X X 空间中可以使用“圆圈”划分数据, 在经过了转换之后,在 空间中就线性划分。这是(1)式告诉我我们的。反过来呢?如果新的资料可以使用一条线划分开, 那么原来的资料一定可以使用圆划分开吗?通过下表可以看出,在 Z Z 空间中的不同的线,对应回 空间可能是各式各样不同的曲线, 所以把这些线对应回来之后我们就知道在 X X 空间可以用哪些曲线来做不同的分类器, 有可能是正圆,椭圆,双曲线等等:
可以看到使用上面的特征转换得到了 X X 空间中的二次曲线分类器是有限制的,圆心是原点 。进一步如果想要得到 X X 空间中所有的二次曲线分类器,那就需要重新定义上面更复杂一点的特征转换: ,得到新的 Z Z 空间(6维), 空间中的每一条直线,对应原来空间中的一个二次的曲线;原来 X X 空间中的任意二次曲线,也对应到 空间中的一条直线。
所以我们现在有了对数据进行分类的新的思路或者是新的假设集:先把原始的数据(例如是二维的)通过某个特征转换(例如 Φ2(x) Φ 2 ( x ) , 其中 2 2 表示二次转换)映射到 空间, 在 Z Z 空间中使用某个线性的模型得到线性的分类器 , 这样就可以得到在 X X 空间中任意形状的二次分类器。
举个例子:
例如在 X X 空间中需要一个如下的“斜椭圆”才能正确的划分数据:
。
现在看看是不是可以使用 6 6 维的
空间 (1,x1,x2,x1x2,x21,x22) ( 1 , x 1 , x 2 , x 1 x 2 , x 1 2 , x 2 2 ) 中的一条直线做到。经过配参数可以得到相对应的 Z Z 空间中的直线的参数为
。所以 Z Z 空间中的每一条线,可以帮助我们实现某一个在
空间中对应的分类方式。
这一小节的思想其实不难,不知道为什么我想说清楚却觉得很难。总结下:为了得到更复杂的分类器,不单单只是线性的,我们要做的就是进行特征转换,想要得到更复杂的分类器就进行更复杂的特征转换。在转换后的高维空间中使用线性模型对转换后的特征进行分类, 就可以得到对应于原始的空间中任意形状的分类器。
2 - Nonlinear Transform
现在我们已经得到,在上节中建立的6维的特征转化下, Z Z 空间(
维)中的所有的直线可以对应到 X X 空间(
维)中的所有的二次曲线。(这里的X是二维空间, Z是六维的空间)。所以如果在 Z Z 空间中可以找到一个好的分隔线,那么就对应到在
空间中的一个好的二次曲线。所谓好的分割线就是指能够正确划分 × × 和 ? ? 的线。
所以我们现在的任务是在 Z Z 空间中找到一条好的“线”。目前我们会的是如何在
空间中使用已知的数据 {
(xn,yn)} { ( x n , y n ) } 得到一个好的分割线,所以我们只要将 X X 空间中的数据通过某个特征转换, 例如,
映射到 Z Z 空间, 这样就可以使用任何的线性的二元分类方法在
空间使用数据 {
(zn=Φ2(xn),yn)} { ( z n = Φ 2 ( x n ) , y n ) } 来找一个好的分割线。
2.1 - 非线性转换的基本步骤
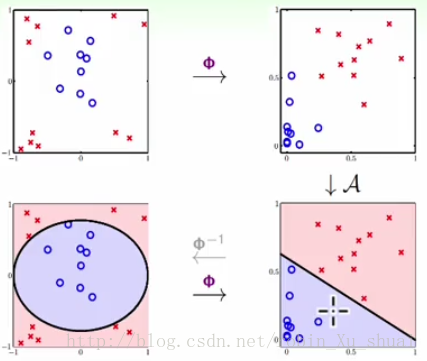
- 将 X X 空间中的资料通过某一个转换 映射到 Z空间 Z 空 间 (高维空间),(左上图 ? ? 右上图)
- 在 Z Z 空间中利用数据 使用任何线性分类的算法 A A 得到一个好的分类器 。(右上图 ? ? 右下图)
- 得到分类器 g(x)=sign(w~T Φ(x)) g ( x ) = s i g n ( w ~ T Φ ( x ) ) 。当一个 X X 空间中的新的数据点要确定类别的时候,同样先对该数据点使用变换 映射至 Z Z 空间,在 空间中得到分类的结果。(左下图 ? ? 右下图)
2.2 - 非线性模型
非线性的转换 + 线性的模型 = 非线性的模型。
非线性的模型需要考虑的两个问题:
- 使用什么样的特征转换,或者说转换到什么样的 Z Z 空间中;
- 使用什么样的线性模型,或者说是使用什么算法。
所以当 算法, pocket p o c k e t 算法, linear regression l i n e a r r e g r e s s i o n 或者是 logistic regression l o g i s t i c r e g r e s s i o n 算法配合一个二次的特征转换,就可以得到二次的 PLA P L A 算法, 二次的 pocket p o c k e t 算法,二次的 linear regression l i n e a r r e g r e s s i o n 或者是二次的 logistic regression l o g i s t i c r e g r e s s i o n 算法;当配合三次的特征转换就有了三次的 PLA P L A 算法, … … 。也就是说只是换一个空间做 linear learning l i n e a r l e a r n i n g 。
2.3 - 一个非线性模型的实例

在机器学习里面有一个很著名也是很基础的应用就是手写数字的识别。在这里我们考虑一种比较原始的方法来区分数字 1 1 ,即做一个二分类的问题:给定一个数字,判定是
或者不是 1 1 。
机器学习的
分为两种, 一种是 concrete c o n c r e t e 的,即有很丰富的物理意义;一种是 raw r a w ,即原始收集来的数据。对于 raw r a w 类型的资料,可以使用专业的知识变为 concrete c o n c r e t e 。例如对于以上的问题,我们收集到的资料是像素级别的, 即每一个手写数字使用一个32 × × 32的像素矩阵表示(是 raw r a w 类型的)。我们可以通过对问题的认识( domain knowledge d o m a i n k n o w l e d g e )从中提取特征。例如对于上述问题我们可以考虑对称性和密度:因为数字 1 1 是比较对称的,数字
的像素密度是比较低的。所以我们就将原来的32 × × 32维的特征转换为了2维的特征: (对称性,密度) ( 对 称 性 , 密 度 ) , 这就对应于一个特征转化 Φ Φ 。 从左上图 ? ? 右上图描述了这个过程, 每一张图片变为了二维空间中的一个点。此时的特征就是 concrete c o n c r e t e 类型的。原来的32 × × 32维的特征现在通过转换 Φ Φ 变为2维的, 所以可以使用线性的算法进行分类。(右上图 ? ? 右下图)。那么对于测试集中的数据(左下图),同样我们先提取它们的两个特征, 密度和对称性 密 度 和 对 称 性 ,在这两个维度的空间中进行分类。

2.4 - A question
现在假设X空间中特征的维度不再是 2 2 , 而是 ,现在在X空间中做二次转换 Φ2 Φ 2 ,那么转换后的Z空间的维度是多少?
- 二次项的个数: Cd2+d C 2 d + d
- 一次项的个数: d d
- 常数项的个数:
Z Z 空间的维度是: 。
3 - Price of Nonlinear Transform
3.1 - Computation or Storage Price
接着上面提到的问题,原始的 X X 空间中特征的维度是
,如果现在要做 Q Q -次的多项式转换
, 那么转换之后的空间的维度可以表示如下:
从 d d 个特征中找出所有低于 次的组合,允许重复。所以 Z Z 空间的维度是 。例如原始的 X X 空间中的维度为2,特征转换为 , 即经过一个 50 50 次多项式的特征转换,那么经过计算可以得到新的 Z Z 空间的大小是1325维的。这其中就带来了一个重要的问题,你的数据量够不够支撑这个1000多维的空间, 在2维的空间中,可能20个样本就够了, 但是在一个1000维的空间中,20个样本是肯定不够的。
这需要付出很大的代价 :
- 进行特征转换的计算量是非常庞大的。每一个样本都要从 d d 维转换为 维。
- 在使用线性的模型求解 w w 的时候, 不再是 d d 个,而是 量级个。例如, linear regression l i n e a r r e g r e s s i o n 中的解析解需要求解 (1+d~)×(1+d~) ( 1 + d ~ ) × ( 1 + d ~ ) 维的矩阵的伪逆矩阵。
- 储蓄上需要 1+d~ 1 + d ~ 的空间而不再是 d d 。
3.2 - Overfitting
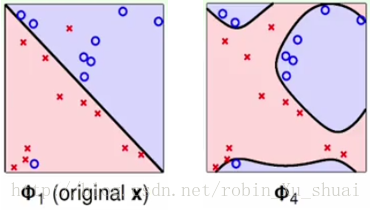
如上图分别是使用原始的数据(经过 转换)和经过特征转换(使用 Φ4 Φ 4 转换成四次多项式)的数据来进行分类的结果。虽然右图的 Ein(g)=0 E i n ( g ) = 0 ,即在训练集上的误差为0, 但是我们认为左边的划分是更好的。
机器学习关心的两个核心问题:
能不能确保 Eout(g) E o u t ( g ) 和 Ein(g) E i n ( g ) 足够的接近(要求模型足够简单)
能不能做到使得 Ein(g) E i n ( g ) 足够小(要求模型足够复杂)
当使用不同的假设函数–是2次的,还是4次的,对这两个核心问题的侧重是不一样的。当进行特征转换的时候,如果 Q Q 很大,即使用非常复杂的特征转换,此时问题2能够很好的解决,但是问题1不能得到保证;如果 很小,即使用很简单的特征转换或者直接使用原始的数据来进行 learning l e a r n i n g ,此时问题1能够很好的解决,但是问题2不能得到保证。这是 machine learning m a c h i n e l e a r n i n g 中最重要的一个 tradeoff t r a d e o f f 。
所以问题来了, 如何选择合适的特征转换 Φ Φ ?
4 - Structured Hypothesis Sets
4.1 - Polynomial Transform
对多项式特征变换给一个“递归”的定义:
以下分别给出的是 0 0 维的变换,
维的变换…
即:
Q Q 次多项式变换 = ( 次多项式变换 + 所有的 Q Q 次式)。
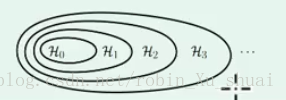
所以可以得到如下的关系, 其中
表示的是 Hypothesis set H y p o t h e s i s s e t (可以简单的理解为可用的模型), 后一个变换的假设集包含前一个变换的假设集(新添加的项的系数设置为0即可)。
可以得到如下的 Hypothesis set structure H y p o t h e s i s s e t s t r u c t u r e
进一步的分析可以得到:
当 hypothesis h y p o t h e s i s 变多的时候,选择变多了, 在这些增加的选择中,可能会找到一个 hypothesis h y p o t h e s i s 有更小的 Ein E i n ,所以 Ein E i n 就会下降,但是如果没有找到更好的,但是起码会和原来的是一样的。所以 Ein E i n 应该是会一直下降的。
根据最后的两个不等式得到机器学习中一个很重要的图:
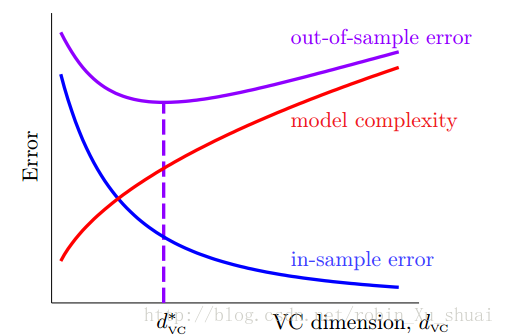
从上面的图可以看到: Ein E i n 随着 Hypothesis Set H y p o t h e s i s S e t 的复杂度的提高而下降;但是模型的复杂度会随之上升。我们最关心的 Eout E o u t 先下降后上升。所以使用一个高维度的变换很容易使得 Ein E i n 很小,但是 Eout E o u t 却会很高, 因为模型的复杂度太大了。最佳的做法是先试用简单的模型, 如果这个时候 Ein E i n 已经很小了, 那么就可以将这个模型作为最终的模型;否则的话, 逐步试用较为复杂的特征转换。
5 - Summary
本篇讲述了非线性变换的流程,使得原来针对的线性的算法可以应用到非线性可分的情形。需要做的事情仅仅是通过一个特征转换 Φ Φ 将低维空间(原来的 X X 空间)中的特征转化到高维空间 中,在 Z Z 空间中使用线性的分类算法即可。虽然这看起来非常的 , 但是实际上是要付出模型复杂度的代价的。所以我们最安全的做法就是:先使用简单的模型。