数学知识——概率统计（5）：单变量统计量：期望和方差_综合

描述量：选出来的、能描述随机变量主要特征的量

统计学家将全面的概率分布信息量投射到某几个量上，来代表随机变量的主要特征，从而掌握该随机变量的主要“性能”。这样的一些量称为随机变量的描述量(descriptor)。
（是不是有些类似降维？又好似用到了奥卡姆剃刀原理）

比如期望用于表示分布的中心位置，方差用于表示分布的分散程度等等。这些描述量可以迅速的传递其概率分布的一些主要信息，允许我们在深入研究之前，先对其特征有一个大概了解。

在现实生活中，我们往往对未知事件有一个预期，也就是我们的期望。
在概率论中，我们更加定量的对未知结果进行预估。根据概率分布，我们以概率值为权重，加权平均所有可能的取值，来获得了该随机变量的期望(expectation)：

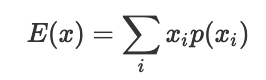
在这里插入图片描述
期望是在事件还没确定时，根据概率，对平均结果的估计。通过了解期望，也就了解了这个随机变量。

注意：（期望与均值的区别）
如果事件发生，结果并不是期望值。
但是，如果重复进行大量实验，其结果的平均值会趋近期望值。
需要注意的是，我们将期望写成E(X)，这表示的是一个数值，而不是一个随机变量的函数。

注：期望和条件期望

在这里插入图片描述

如果说期望表示的是分布的中心位置，那么方差就是分布的离散程度。方差越大，说明随机变量取值越离散。

数学上，我们用方差来代表一组数据或者某个概率分布的离散程度。可见，方差是独立于期望的另一个对分布的度量。两个分布，完全可能有相同的期望，而方差不同。

对于一个随机变量X来说，它的方差为:
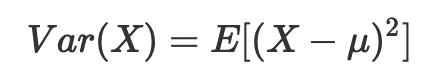
在这里插入图片描述
其中，μ 表示 X 的期望值，即 μ=E(X)。

方差概念背后的逻辑很简单。一个取值与期望值的“距离”用两者差的平方表示。该平方值表示取值与分布中心的偏差程度。
我们根据概率对该平方进行加权平均，也就获得整体的离散程度——方差。

方差的平方根称为标准差(standard deviation, 简写std)。我们常用σ表示标准差：
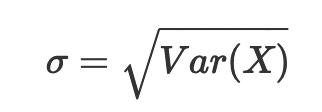
在这里插入图片描述
标准差也表示分布的离散程度。

为了表达分布的密度曲线向左或者向右的倾斜特征，引入一个新的描述量，斜度(skewness)，定义如下：

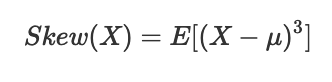
在这里插入图片描述

在这里插入图片描述
观察方差和斜度的定义，都是X的函数的期望。它们的区别只在于函数的形式，即(X?μ)的乘方次数不同。方差为2次方，斜度为3次方。

上面的描述量都可以归为**“矩”(moment)的一族描述量。类似于方差和斜度这样的，它们都是(X?μ)乘方的期望，称为中心矩(central moment)**。E[(x?μ)^k]称为k阶中心矩，表示为μ_k，其中k = 2, 3, 4, …

还有另一种是原点矩(moment about the origin)，是X乘方的期望。 E[X^k]称为k阶原点矩，表示为μ′_k，其中k = 1, 2, 3, …
期望是一阶原点矩:
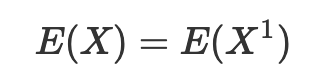
在这里插入图片描述

更多细节可以参考：