数学知识——概率统计（11）小结：多个变量之间的关系描述_综合

之前提到过描述单个随机变量的一些工具，比如正针对整体总体细节的“分布”、针对总体概述的各种统计量（期望、方差等），也提到过针多元随机变量的描述量：协方差和相关系数，现在此总结下多个变量之间关系的研究。

注：针对机器学习的问题，“变量”可以直接理解为“特征”。

1. 散点图

研究两个变量之间关系的最简单方法是散点图（scatter plot）。但好的散点图的绘制并不简单。

注：可以将数据进行抖动（jittering），即加入随机噪音弥补四舍五入的效果，以减少丢失信息对散点图的影响。
但是，抖动数据通常只应用于视觉效果，你应该避免在分析时使用经过抖动处理的数据。
在这里插入图片描述
即便经过了抖动处理，散点图也不是展示数据的最佳方法。图中有很多重叠的点，遮盖了密集部分的数据，使离群值显得特别突出。这种效果称为饱和（saturation）。

2. 描述关系特征

散点图能让我们对变量关系有个大体了解，而其他可视化方法则可以让我们更深入地了解变量关系的本质。一种方法是对一个变量进行分区，绘制另一个变量的百分位数。

3. 相关性分析

相关性（correlation）是一个统计量，用于量化两个变量之间关系的强弱。

度量相关性的困难之处在于，我们需要比较的变量通常使用不同的单位。即便变量使用相同的单位，也可能来自不同的分布。

这些问题有两个常见的解决方法。

将每个值都转换为标准分数（standard score），即其偏离均值的标准差数。这种转换会产生“Pearson乘积矩相关系数”。

将每个值都转换为秩，即其在所有值的排序列表中的索引。这种转换会产生“Spearman秩相关系数”。

3.1 协方差

协方差（covariance）可以度量两个变量共同变化的趋势。
对于随机变量X和Y，两者的协方差定义如下：
Cov[X,Y] = E[(X-μ_x)(Y-μ_y)]，（中括号只是一种约定俗成的表示手段）可以这样理解：
在这里插入图片描述

协方差公式中包含的含义：
协方差为正，表示X增大时，Y也增大——正相关性；
协方差为负，表示X增大时，Y倾向于减小——负相关性；
协方差为0时，表示X增大，Y没有明显的增大或减小的倾向——两者独立相关。

几点注意：

1.与方差的关系
Var[X] = E[(X-μ)²] = E[(X-μ)(X-μ)] ，其实方差就是一种特殊的协方差

2.协方差矩阵

我们可以引入一个协方差矩阵，将一组变量X₁，X₂，X₃两两之间的协方差用矩阵的形式统一进行表达：

[ 
V[X~1~]      Cov[X~1~X~2~]      Cov[X~2~X~3~]
Cov[X~2~X~1~      V[X~2~]       Cov[X~2~X~3~]
Cov[X~2~X~1~]      Cov[X~3~X~2~]     V[X~3~]     
]

注：看上面的公示就会发现若均值μ都为0 ，则计算会简便很多，所以一般先对变量进行0均值处理（x_i或者y_i减去他们的均值）

3.PCA降维的过程

假设我们研究的对象有两个特征属性X和Y，对 5 个样本进行数据采样的结果如下：

	X	Y
样本1	2	2
样本2	2	6
样本3	4	6
样本4	8	8
样本5	4	8

我们的目标是对其降维，只用一维特征来表示每个样本，只用一维特征来表示每个样本。我们首先将其绘制在二维平面图中进行整体观察：
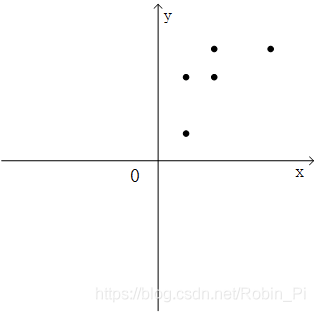
在这里插入图片描述
查看这两个变量的协方差矩阵，

import numpy as np
import matplotlib.pyplot as pltx = [2,2,4,8,4]
y = [2,6,6,8,8]
S = np.vstack((x,y))print(np.cov(S))[[ 6.  4.][ 4.  6.]]

结合之前的二维散点图可以发现5个样本的特征 X 和特征 Y 呈现出正相关性，数据彼此之间存在着影响。

若直接粗暴地去掉一个特征，可行么？则会变成：
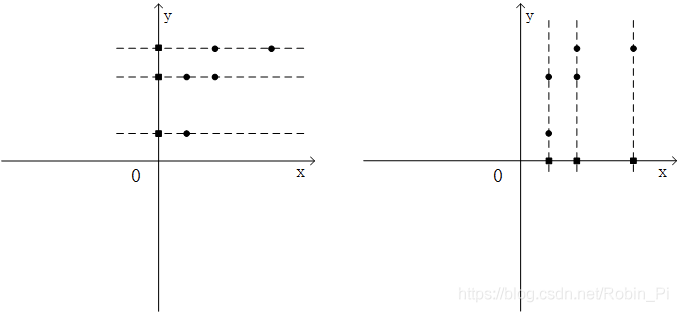在这里插入图片描述显然效果不理想：忽视了数据中的内在结构关系，并且带来了非常明显的信息损失。
（降维——>高维数据向低维进行投影）

一个解决思路便是：

① 去除原始特征的相关性，使用心新的一组特征来表示原始数据
② 然后从新的彼此无关的特征中舍弃不重要的特征，保留较少的特征，实现降维。

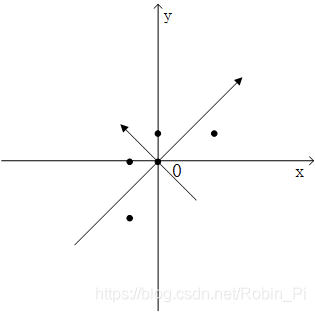
首先，第一点的目的是使用新的特征来对样本来进行描述，为了让这两个新特征满足彼此无关的要求，就需要让这两个新特征的协方差为0，构成的协方差矩阵是一个对角矩阵（原始特征X和Y的协方差不是0，只是一个普通的对称矩阵）

对变量分别进行0均值处理后，通过求解协方差矩阵的特征向量，就可以得到线性无关的特征矩阵（图中两个新的坐标方向）。

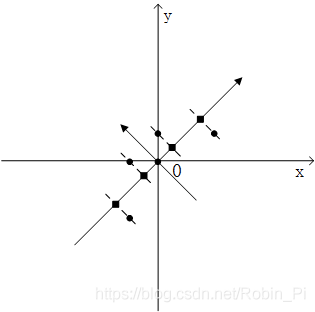
在这里插入图片描述
接下来的工作就是从这两个特征中选取一个作为原始数据的特征表达，其判断标准是方差，方差越大表示这个特征里的数据分布的离散程度就越大，特征所包含的信息量就越大。

在这里插入图片描述

3.2 Pearson相关性

协方差在一些计算中非常有用，但其含义很难解释，因此人们很少将协方差作为摘要统计量。别的不提，协方差的单位是 X 和 Y 的单位乘积，这一点就很难理解。例如，BRFSS数据集中体重和身高的协方差是113千克-厘米，天晓得这是什么意思。
解决这个问题的方法之一是将偏差除以标准差，得到标准分数，然后计算标准分数的乘积。
Pearson相关性容易计算，也易于解释。因为标准分数是无量纲（无单位），所以 ρ 也是无单位的。

非线性关系

如果Pearson相关性接近0，你可能会认为变量之间没有关系，但这个结论并不成立。Pearson相关性只度量了线性（linear）关系。如果变量之间存在非线性关系，那么 ρ 对变量相关性强弱的估计就可能是错误的。

Spearman秩相关

如果变量之间的关系是线性的，而且变量大致符合正态分布，那么Pearson相关性能够很好地说明相关性的强弱。但是离群值会影响Pearson相关性的稳健性。Spearman秩相关能够缓解离群值以及偏斜分布的的影响，也可以用于描述变量的相关性。要计算Spearman相关性，必须计算每个值的秩（rank），即该值在排序样本中的索引。

数学知识——概率统计（11）小结：多个变量之间的关系描述

目录