纯属个人思考,极有可能出错,自行取用
一、Abstract:
使用先验符号知识 -> 改善深度模型的效果
如何使用先验符号知识:图表征网络——将命题公式转化到一个mainfold(空间)。
得到了什么?具有语义可靠的表征(semantically-faithful embedding)——能够在学习的过程中,将命题公式的信息一并加入到模型中,使其获得一定根据规则判断的能力
进一步的工作:阐明为什么这么做能够将知识编写与向量表示学习进行联系
二、Introduction:
目前的Deep Networks:
-
应用领域多、任务丰富:医学图像分类、玩游戏、人脸识别、语音助手等
-
最大的限制:大量的标签数据
-
联系:对于这些需要大量标签的任务,人们往往只需要通过理论知识,使用简洁的符号语言进行表述
-
目标:整合先验知识和神经网络
-
难点:在可扩展和有效的方面面临诸多问题,目前本论文考虑的是使用实值向量对先验知识进行表达,这有助于其更好地被神经网络处理
论文聚焦:
-
先验知识:logic rules 逻辑规则,可表示、可组合并且能够用描述人的知识
-
表示形式:CNF描述转为d-DNNF(具体格式参见另外一篇笔记)
-
知识的处理方法:使用GCN的方法去处理逻辑图,针对于2021年的情况,同样可以考虑GAT等新的GNN模型的使用。
-
知识如何引入:semantic regularization 语义正则项
-
图的类型:异构图,GCN识别节点的异构性,并将逻辑图根据逻辑操作符 AND关系和 OR关系构建表征结构。
Semantic Regularization:

-
里面的Layer 1,2,。。。,n的意思是做n次消 息的传播,因为一次传播只能传播一层的信息, n层之后每个节点才能得到命题公式的逻辑图的 全局信息。
-
命题公式的表达形式: 命题逻辑(非谓词逻辑) 参见第一段
-
Assign如何理解:首先我们根据先验知识会确定模型所需要用到的所有逻辑规则,这些逻辑规则都会对应一个逻辑图,对于规则直接对应的逻辑图我们就认为是一个有命题逻辑构造的命题公式,Assign是一个函数,处理的是来源于模型的输入,比如论文中输入的是一个图像,经过比如CNN网络提取特征等操作后,进而通过处理也会得到一个逻辑图,此时这个逻辑图蕴含了一个命题公式,通过assign方法对该命题公式进行处理,能得到该命题公式是True还是FALSE,也就对应了Formula Assignment,而后对这两个逻辑图进行embedding,对assign为真的embedding与命题公式embedding拉近,assign为加的要拉远,进而将两个embedding的距离作为loss,加入原始的CNN的loss中,作为regularization,核心就在于semantic regularization的使用,如图所示,AND和OR是关键
-
使用d-DNNF:表达能力强,可组合能力强,缺点是指数增长。
-
此前也有使用d-DNNF进行先验知识的引入工作,但是还没有将其与神经网络结合的工作
-
代码: https://github.com/ZiweiXU/LENSR
背景知识和相关工作:
参考另一份笔记
名词解释:
-
Conjunctive Normal Form (CNF): 合取范式
-
Disjuncive Normal Form (DNF): 析取范式
-
Negation Normal Form (NNF): 否定范式 否定范式的特点就是能够定义一个有根节点的有向无环图(Directed Acyclic grapg,DAG),DAG的特点是每一个叶子节点都是命题,命题可以是真也可以是假,p或者?p,并且每个内部节点都是逻辑操作符∧ or ∨。可以看到没有蕴含符号了。
-
Propositional Variables: 命题变量,这里注意指的不是谓词逻辑中的命题公式中的变量x等,而是指的命题本身,因为一套系统可能需要定义许多命题,这些不同的命题本身就是不同的变量,这些变量也是Assign函数的输入。
-
d-DNNF:相较于原有的NNF格式,增加了两个限制,分别是确定性和可分解性 ,确定性指的是要求在∨操作符两边的命题在布尔值上要互相排斥,比如p∨?p,这种意思;其次是 可分解性:可分解性针对的是∧操作,要求合取操作的两边的命题变量不存在交集合,比如(p∨q)∧(m∨?n)。
-
Clauses:该词语的意思是子句,通常指代的是CNF或DNF中的合取或析取的每一个小部分,比如(p∨q)∧(m∨?n)这个合取范式就具有两个子句分别是(p∨q)和(m∨?n)。其实可以理解的是每一个子句是我们进行判断的时候的一个最小单元,也可以看做是某件事情成立的条件之一,把多个条件进行组合,可以看做是构成了一个合取范式,然后就能判断一个事情的真假了。
普通的命题逻辑的有向无环图形式、CNF、d-DNNF具体的例子如下:

****注意****
论文中指明了,在计算的时候只需要去构造CNF的形式,d-DNNF的形式通过一个c2d的命题公式编译器去实现,论文的代码中有一个linux版本的程序,如果在Windows去运行需要找一个Windows下的程序。
三、算法思考(具体的算法参考论文)

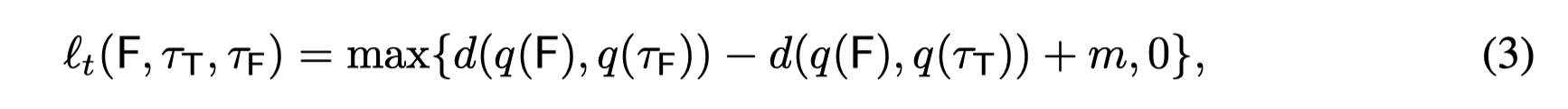
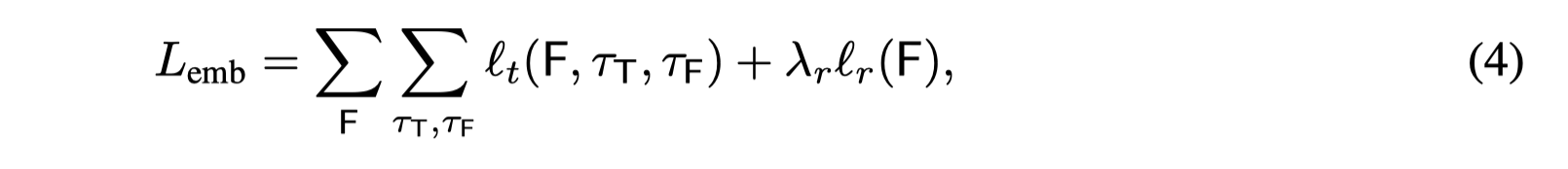
1、可以根据图中的(4)式看到,semantic regularization针对的是Formulae做的,也就是比如 人戴着眼镜,这一个命题公式的表示本身,而不是经过assign function操作后的输入的内容。那么问题来了
为什么对Formulae进行embedding后,构造成正则项可以在原有的比如图像预测的CNN模型中引入知识?
我是这么理解的,首先以往的正则项,常见的l2,l1正则项等,目的仅仅是单纯的防止过拟合或者是其他的问题,而这种传统的正则项的方法并不能够对原有的模型融入新的特征,因为这一类正则项的产生是相对固定的,比如当前参数是多少,直接通过固定的l2正则项求解公式就能得到。
!!!!!!!!!!!!!!!!
注意这里的理解出现了问题!根据实验设计和算法设计来看,算法流程中
embeder的训练和预测模型的训练是分开的,先训练embeder,使每个命题能够得到固定的embedding。这三个式子讲明的是embeder如何训练,也就是说semantic regularization是在embeder的训练过程中使用的。传统的正则项的解释按照下面的理解没有问题
那么首先思考,
为什么传统的正则项能够防止过拟合?我认为是如果不加正则项,传统的比如图像识别任务的loss 使用的是预测结果和标签的差异,反向传播的时候目的是让这两个值接近,那么在参数足够,loss持续下降的时候,就会导致loss接近于0,导致过拟合,而如果在计算loss的时候加入正则项,相当于是在反向传播的梯度中加入了一个与参数相关的值,让其除了往正确的标签方向下降之外,还需要向其的正则项的值得方向下降,这样就达到了对模型参数的一个约束,能够避免过拟合的发生。
虽然这种方式没有引入其他的知识信息,但是它本身也是一种限制,只不过这种限制本身是一个固定的数;包括贝叶斯方法,其实也可以看做是一个正则项,只不过它加入了一定的先验信息。
这一段理解出现偏差,看另一段解释
因此,我猜测作者受到正则项方法本身是一种约束规则的方式,考虑使用规则直接作为正则项的方式去对原有的方法做约束,约束的时候相当于是对不同的formulae通过一个GNN方式进行编码,这个编码再经过它的semantic regularization的计算方式变成一个值,这就对不同的formulae得到了不同的值,那么根据这种regularization的方式在对原有方法进行训练的时候就能够让模型在对输入进行预测或分类的同时能够与特定的规则进行匹配,这个时候就会在原有的反向传播的基础上再往各自所满足的规则上靠近,进而进一步的对不同的输入进行区分,从而使模型具有运用规则的能力,至此来达到规则的软化。
使用semantic regularization的方式固然是好的,但是又要考虑到一点,因为规则是通过GNN学习得到的,在使用semantic regularization作为loss 反向传播的时候虽然看上去是向规则靠拢了,注意哈,这里向规则靠拢也只是在预测基本准确之后才朝着规则靠拢,因为一开始的loss下降只会帮助预测效果,而formulae的GNN模型的下降是乱降的,在预测基本准确之后呢,保证预测效果的同时再去训练这个Formulae的GNN,但是这里忽略了一个问题就是前一步的GNN映射到的embedding空间和原有方法执行预测或分类任务的空间,并不是一个空间,上面的预测的效果的loss基本不降之后,下面的Formulae的GNN通过计算得到的loss并不能对GNN进行很好的训练,因为下面的loss是随机的,下降的方向也是随机的,虽然每个Formula计算的regularization不同,但是每次下降都没有目标这其实就是不在一个空间导致的。
不在一个空间
就会导致一个问题,在原有的方法加入semantic regularization作为loss的一部分,在计算梯度的时候使用的是执行预测或分类的模型的参数,进行反向传播的时候也是针对的原有的模型,使用这样的梯度对处理Formulae的GNN模型进行传播的时候就会导致处理
Formulae的GNN模型不知道自己应该去往哪个方向,我猜会导致模型不收敛。
因此作者进一步的思考,提出了针对于训练的Triplet loss,这个loss设计的目的是
将原有的模型和Formulae的GNN模型的参数进行关联,并且能够让其处在同一空间下。关联两个embedding的最好的方式就是求两个embedding的距离,因此作者考虑使用了Euclidean distance(欧氏距离),
那么求距离有一个问题就是,求谁和谁的距离?那么首先就是Formulae本身的embedding,Formulae的embedding蕴含的信息最全,因为当一个命题公式成立的时候,它可能只是其中的部分条件为真,比如(如果一个人握着方向盘)或(一个人握着汽车档把)那么(这个人在汽车内部),这个描述里,当该命题公式为真的时候只需要握着方向盘或者档把就可以了,因此Formulae的embedding信息最为全面,而原有的模型对输入运用规则判断的时候可能只会用到命题公式的一部分条件,但是此时足以判断命题公式为真,因此这个时候就考虑将原有的模型在梯度传播的时候朝着Formulae的GNN模型所定义的embedding空间去靠,从而达到效果,而如果原有的模型预测出来的是错误的assignments,那么就要让其原理Formulae的空间,因此上述图片中的(3)式的计算τF和τT只会同时存在一个,而不会两个都存在,谁存在就用谁的值计算距离即可。那么为什么要和0相比较,原因就是assignments为真的时候原有模型的参数得到的embedding要靠近,这个时候以loss本身的功能来看,loss就应该为0,因为此时认为他已经和Formulae在同一位置了,不需要调整,而如果assignments是错的,那么加入一个loss,使得原有的模型梯度传播的时候会受到这个loss影响,让其embedding朝着与Formulae的embedding的方向去靠近。
因此结合训练和融入规则信息的方式,作者最终的loss是prediction loss和triplet loss和semantic regularization的联合loss,其中triplet loss和semantic regularization loss都是融入先验知识模块的内容,triplet loss用于使处于同一空间,semantic regularization目的是将先验知识融入原有模型。
****注意****
上述内容的分析我是以实际情况为基础进行分析的,而论文中对上述的2,3,4式式根据只是针对训练Formulae的embedder分析的,因此4式中出现了两个求和,指代了所有的formulae和所有的assignments的情况,但是总的来看,想表达的意思是不变的。
正确的理解方式
首先很显然,semantic regularization的目的是在训练embeder的时候能够让表达不同规则的∧和∨的数量,以及他们各自具有的不同信息,从而能够在传播梯度的时候朝着不同的方向去下降,达到对Formulae embeder在计算embedding的时候的约束,如果是跟随着预测模块一同训练(假定不加入triplet loss),很明显,这里的semantic regularization自身还没有确定具体的方向,那么这个时候embeder在更新的时候还掺杂了预测模型的loss,预测模型掺杂了embeder的loss,肯定是不合理,
因此,考虑的是分开训练,分开训练的时候要考虑的问题就是得到的logic embedding如何区分的问题,这就涉及到正负样本了,因此在给定的命题公式下,要找出他们各自的assignments,然后计算Formulae的embedding和他们assignments的差异,使得不满足assignments的embedding要远离Formulae的embedding,满足的assignments要靠近Formulae的embedding,因此又增加了triplet loss,在这一情况下,训练embeder的时候加入semantic regularization就能保证进一步的增强logic embedding的表示能力,才是合理的。
2、最终的训练loss设置

理解错误的内容
可以看到(5)式并没有体现出semantic regularization和triplet loss,,那么为什么呢?
很显然,(5)式的目的是表达semantic regularization和triplet loss 的思想,虽然形式不一样但是作用的目的达到了,如果没有前面的2,3,4三个式子就没有办法化简为(5)式。
分解:
Fx可以看做是根据输入的数据的标签匹配到的Formulae,h(x)呢则是原有的模型输出得到的一个相关的预测,也可以理解为是assignments,二者相减求2范式的平方,目的其实就是计算Formulae和预测得到的assignments的embedding的距离,在计算了距离的同时,也蕴含了semantic regularization。其实上面2,3,4中的3式本身也蕴含了一定的semantic regularization,只不过两者结合效果更好,因为3式为0的时候loss就是F本身,3式不为0的时候是在F的基础上加了一个值,F和F+3式其实蕴含的就是梯度下降的一个大小的问题。简化为5中的logic loss之后,模型的训练过程其实可以理解为,一开始可能预测是不正确的,在5的loss下会朝着预测正确进行移动,同时下面的距离也在拉近,注意一开始不论预测的是正确的还是错的,距离都会比较大,这个loss起作用是在,当预测是基本正确了的时候,如果loss仍然较大,就说明当前的预测内容的embedding和规则本身的embedding有较大的的偏差,这个时候loss就会忘规则的embedding方向拉近,同时规则的embedding也会向目前预测正确的embedding拉近,最后loss基本不再下降后,就可以认为预测得到的embedding也蕴含了规则的embedding信息。因此可以看到,当预测的loss下降的差不多的时候,就可以认为原有的模型的embedding应该就是formulae的embedding,而这个时候下面的formulae自身的GNN的embedding和上面的embedding还不匹配,因此就要继续通过求距离的方式让二者拉近,从而达到规则约束的效果,这个距离的拉近过程。
正确的理解
很明显因为embeder的目的是要得到标准的Formulae的logic embedding,预测模型加入embeder的目的是构建联合loss的,如果在预测模型中,预测得到的内容能够代表一个formula,那么这个情况下将其与embeder的标准embedding进行比较,计算距离,通过加入这一loss可以在预测准确的情况下,进一步的拉近预测模块的embedding和logic embedding的距离,从而将规则信息进行了融入,semantic regularization是通过训练好的embeder构造的logic embedding后,通过距离的计算,再通过联合loss间接作用的。
3、核心思考!关于regularization的思考
正则项本身在一开始梯度传播的时候其实是不起什么作用的,关键是在下降到一定程度之后,预测内容正确了,但是regularization的值还没有下降,在这种情况下,保证预测内容没问题的情况下,朝着regularization的约束移动,从而保证了regularization对原有模型的一个约束。这才是regularization的意义,也就是设计
regularization的时候不应该盯着一开始训练模型不正确,而是训练模型基本正确之后如何去优化,如果是一个可学习的regularization也应该看的是学习完成之后,如何进一步的去学习regularization的参数 。
4、训练数据的含义
根据前面的理解,很显然,原有的处理模型在设计的时候,要考虑规则的部分,也就是embedding部分,我的理解是原有的模型的在给出预测结果之前的embedding代表了所有命题公式中关系的概率,其实应该就是所有的子句,如果有1000个子句,比如”人戴了帽子”,“人握着方向盘”……,那么embedding层就会计算得到1000个不同的embedding分别代表不同的子句,把这些(值为true)
成立的子句进行合取,就可以得到一个logic graph,对这种logic graph使用下面的GNN方法进行处理,得到其的embedding,再与Formulae的embedding求距离,得到logic loss。
四、实验:如何结合故障发现规则进行设计
1、人工数据集——SYnthetic Dataset
LENSR:3层,每层50个隐藏单元,输出为100维向量
任务模型:2层 每层150个隐藏单元
要训练embeder 也就是LENSR部分,
首先要设计命题公式,作者设计命题变量有nv个,每个规则的最大深度为dm,然后通过手工构造,设计了三个数据集,分为 low、moderate和high三种命题公式数据集,注意low和moderate通过手工枚举就可以得到满足的assignments和不满足的assignments,针对于high的命题公式数据集,使用了python-sat的方式进行进行求解,只保留5个满足的和5个不满足的assignments。最后分别用三个数据及进行训练,得到的embeder的表示效果如下

How to train:
首先是根据手工构造的数据集,将assignments和formulae构造成logic graph,也就是有向无环图,通过embder进行编码,最后针对于每一个formula或assignments都会得到一个100维的embedding向量,训练embeder的时候loss就是打标签,远离和接近,此时训练好embeder之后,再开始预测模型的训练,预测模型的数据就是embeder中assignments,只不过不构造成图的形式,而是要根据assignments直接给出它满足哪一个命题公式,进而计算分类的loss,然后再反向传播进行训练,这里的主要目的是测验d-DNNF相对于其余命题公式表达成有向无环图的表示能力。
2、真是场景数据集——Visual Relation Prediction
A、首先是介绍一下视觉关系数据集是如何运作的
VRD-Visual Relation DataSet 包含5000张图片,这5000张图片中共包含100个目标以及70个标识的谓词(关系),针对于每张图像,模型会识别其中的目标,对这些目标进行两两提取,并推测他们之间的空间关系,如果这两个object之间没有任何的注释/标签,则认为两个object之间没有关系-‘no relation’。
Propositions and Constraints;
Proposition:
-
Existence Propositions: 如果图像中存在某个object,就会构造一个p=exist(person),意思是存在一个人。那么会带来一个思考,使用该数据集的目标是预测关系,而存在命题不是预测范围,也就是需要识别的内容,如何识别呢?必然是使用目标检测算法对图像进行划分,那么就会得到各个object在图像上的划分。
-
Visual Relation Propositions: 视觉关系指的关系结合他们的subject和object,分别指的是主语和目标,subject和object本质都是object,只是在判断关系的时候区分了一下主次,比如人戴了太阳镜,据此呢,可以构造一个命题,记做p=wear(person,glasses)
-
Spatial Relation Propositions:视觉关系成立的时候必须要满足一定的空间位置,比如人戴了太阳镜,就必须要能够判断在图像中太阳镜把人的眼睛遮住,因此进一步定义了空间关系的限制,总共设计了10种类型的空间关系。记做p=in(glasses,person),意思是太阳镜在人的里面,其实就是遮住了眼睛。并且,在实际使用的时候,每一个空间关系命题必然会结合一个视觉关系命题出现
Constraints:
-
Existence Constraints: p(sub,obj)=>(exist(sub)∧exist(obj)
-
Spatial Constraints: wear(person,glasses)=>in(glasses,person)
由上述的命题和约束,对于每一个图像都有: 构造一组子句,
 ,其中cij是一组命题的析取式,每一个子句cij代表了图像中的一个约束,,每个命题pjk代表了一个图像中的关系(关系包存在以及空间关系,析取式不是简单的将式子进行析取,而是通过将Constraints转化为析取得到的析取式,里面有’非命题’,比如 非wear(a,b) 析取 ( exist(a) 合取 exist(b) ),k指的是命题索引,在实验中,根据标记好的信息,可以对每个图像直接构造关系以及约束,给予这些构造好的内容,每一个图像可以包括50-1000个子句和变量。最终,所有的图像经过合取构造了一个公式F,
,其中cij是一组命题的析取式,每一个子句cij代表了图像中的一个约束,,每个命题pjk代表了一个图像中的关系(关系包存在以及空间关系,析取式不是简单的将式子进行析取,而是通过将Constraints转化为析取得到的析取式,里面有’非命题’,比如 非wear(a,b) 析取 ( exist(a) 合取 exist(b) ),k指的是命题索引,在实验中,根据标记好的信息,可以对每个图像直接构造关系以及约束,给予这些构造好的内容,每一个图像可以包括50-1000个子句和变量。最终,所有的图像经过合取构造了一个公式F,
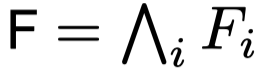 。注意Fi是一个子句的集合,并没有指点他是析取还是合取,也就是说Fi只蕴含了当前图像有哪些约束,在构造公式F的时候对所有的Fi进行合取,其实就是对Fi中的每个约束cij进行合取,最终得到一个完整的大公式,这个大公式是需要化简的,因为其中会有比较多的重复内容,对这些重复内容进行合并,最终才能得到当前的视觉关系系统的完整的命题公式。每一图片都可以看做是F的一个satisfied assignment,因为最终决定Fi是真是假的是其中的cij,决定cij的是析取式,因此较为灵活。
。注意Fi是一个子句的集合,并没有指点他是析取还是合取,也就是说Fi只蕴含了当前图像有哪些约束,在构造公式F的时候对所有的Fi进行合取,其实就是对Fi中的每个约束cij进行合取,最终得到一个完整的大公式,这个大公式是需要化简的,因为其中会有比较多的重复内容,对这些重复内容进行合并,最终才能得到当前的视觉关系系统的完整的命题公式。每一图片都可以看做是F的一个satisfied assignment,因为最终决定Fi是真是假的是其中的cij,决定cij的是析取式,因此较为灵活。
 ,其中cij是一组命题的析取式,每一个子句cij代表了图像中的一个约束,,每个命题pjk代表了一个图像中的关系(关系包存在以及空间关系,析取式不是简单的将式子进行析取,而是通过将Constraints转化为析取得到的析取式,里面有’非命题’,比如 非wear(a,b) 析取 ( exist(a) 合取 exist(b) ),k指的是命题索引,在实验中,根据标记好的信息,可以对每个图像直接构造关系以及约束,给予这些构造好的内容,每一个图像可以包括50-1000个子句和变量。最终,所有的图像经过合取构造了一个公式F,
,其中cij是一组命题的析取式,每一个子句cij代表了图像中的一个约束,,每个命题pjk代表了一个图像中的关系(关系包存在以及空间关系,析取式不是简单的将式子进行析取,而是通过将Constraints转化为析取得到的析取式,里面有’非命题’,比如 非wear(a,b) 析取 ( exist(a) 合取 exist(b) ),k指的是命题索引,在实验中,根据标记好的信息,可以对每个图像直接构造关系以及约束,给予这些构造好的内容,每一个图像可以包括50-1000个子句和变量。最终,所有的图像经过合取构造了一个公式F,
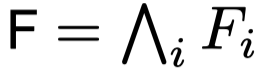 。注意Fi是一个子句的集合,并没有指点他是析取还是合取,也就是说Fi只蕴含了当前图像有哪些约束,在构造公式F的时候对所有的Fi进行合取,其实就是对Fi中的每个约束cij进行合取,最终得到一个完整的大公式,这个大公式是需要化简的,因为其中会有比较多的重复内容,对这些重复内容进行合并,最终才能得到当前的视觉关系系统的完整的命题公式。每一图片都可以看做是F的一个satisfied assignment,因为最终决定Fi是真是假的是其中的cij,决定cij的是析取式,因此较为灵活。
。注意Fi是一个子句的集合,并没有指点他是析取还是合取,也就是说Fi只蕴含了当前图像有哪些约束,在构造公式F的时候对所有的Fi进行合取,其实就是对Fi中的每个约束cij进行合取,最终得到一个完整的大公式,这个大公式是需要化简的,因为其中会有比较多的重复内容,对这些重复内容进行合并,最终才能得到当前的视觉关系系统的完整的命题公式。每一图片都可以看做是F的一个satisfied assignment,因为最终决定Fi是真是假的是其中的cij,决定cij的是析取式,因此较为灵活。
B、如何针对VRD数据集进行训练
首先训练embeder,然后固定住embeder训练目标神经网络模型。具体的根据论文内容的划线部分进行个人拆解:


可以看到训练部分的处理方式是,对于每一张训练图像,根据他的标签,可以得到一个fi,也就是一个子句集,遍历子句集,每个子句集包含一组关系,每个关系其实就指代了一个命题,命题里面包含的是object和predicate。那么每个图像的fi具体是如何根据标签得到的呢?首先是需要有一个object detection算法,识别各个object,以及获取他们的位置信息,根据这个内容可以得到一个一个的关系,
此时不包括视觉关系,因此此时fi是不完整的,论文中给出的关系的描述是一个陈述短语,而不是存储命题逻辑的表达式,
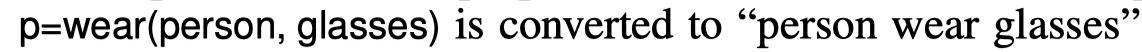 ,尽管二者都可以代表一个关系,但是表达成word的形式,可以通过word embedding增强每个关系的辨识度,以及更好地表达成向量的形式。如果不这么做,对每个关系用object和predicate的one-hot编码,会导致无法扩展的问题,每次扩展都需要生成新的one-hot,并且引入one-hot的先天稀疏的缺陷问题。因此作者使用Glove对每个关系进行embedding,然后将每个关系中的word的embedding相加,进而代表每个关系的embedding。每个图像的最小单位,也就是pjk的关系的embedding确认之后,就开始设计如果根据这些信息进行embeder的训练,训练embeder的时候可以使用图像的视觉关系标签,进一步扩展每个图像的fi,每个图像可以构造satisfied assignments以及unsatisfied assignments,每个图像具体构造多少需要看论文给出的代码,应该属于一个超参数调节。训练的时候是与F也就是前面介绍的所有图像的Fi的合取后的命题公式进行比较,计算距离。训练embeder的时候也是根据每个图像每个图像进行训练,只不过embeder的训练是带视觉关系标签训练的,而预测模型的视觉关系是预测得到的,仅此而已,embeder中计算距离,F其实指的就是图像I确定的公式Fi,Fi和其余assignments的距离,Fi是什么呢?Fi就是命题公式,可以理解为就是一个陈述句。我猜测,代码中就是Fi的命题的陈述句一个规范,其他的assignments是在此基础上修改,比如 exist(person) exist(car) in(person,car) drive(person,car)这个是Fi的结构,其余的unsatisfied结构可以变为 exist(person) exist(car) out(person,car) not_drive(person,car),让这些assignments与命题本身远离,由每个命题确定的Fi其实也可以看做是一个命题的satisfied assignments,只不过说这里他既可以看做命题 也可以看做assignments,不矛盾,目的都是用于未来的推理,每一个图片都可以看做是对这个知识的强化过程。具体的参考代码进一步理解。
,尽管二者都可以代表一个关系,但是表达成word的形式,可以通过word embedding增强每个关系的辨识度,以及更好地表达成向量的形式。如果不这么做,对每个关系用object和predicate的one-hot编码,会导致无法扩展的问题,每次扩展都需要生成新的one-hot,并且引入one-hot的先天稀疏的缺陷问题。因此作者使用Glove对每个关系进行embedding,然后将每个关系中的word的embedding相加,进而代表每个关系的embedding。每个图像的最小单位,也就是pjk的关系的embedding确认之后,就开始设计如果根据这些信息进行embeder的训练,训练embeder的时候可以使用图像的视觉关系标签,进一步扩展每个图像的fi,每个图像可以构造satisfied assignments以及unsatisfied assignments,每个图像具体构造多少需要看论文给出的代码,应该属于一个超参数调节。训练的时候是与F也就是前面介绍的所有图像的Fi的合取后的命题公式进行比较,计算距离。训练embeder的时候也是根据每个图像每个图像进行训练,只不过embeder的训练是带视觉关系标签训练的,而预测模型的视觉关系是预测得到的,仅此而已,embeder中计算距离,F其实指的就是图像I确定的公式Fi,Fi和其余assignments的距离,Fi是什么呢?Fi就是命题公式,可以理解为就是一个陈述句。我猜测,代码中就是Fi的命题的陈述句一个规范,其他的assignments是在此基础上修改,比如 exist(person) exist(car) in(person,car) drive(person,car)这个是Fi的结构,其余的unsatisfied结构可以变为 exist(person) exist(car) out(person,car) not_drive(person,car),让这些assignments与命题本身远离,由每个命题确定的Fi其实也可以看做是一个命题的satisfied assignments,只不过说这里他既可以看做命题 也可以看做assignments,不矛盾,目的都是用于未来的推理,每一个图片都可以看做是对这个知识的强化过程。具体的参考代码进一步理解。
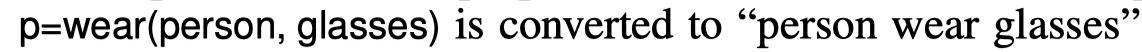 ,尽管二者都可以代表一个关系,但是表达成word的形式,可以通过word embedding增强每个关系的辨识度,以及更好地表达成向量的形式。如果不这么做,对每个关系用object和predicate的one-hot编码,会导致无法扩展的问题,每次扩展都需要生成新的one-hot,并且引入one-hot的先天稀疏的缺陷问题。因此作者使用Glove对每个关系进行embedding,然后将每个关系中的word的embedding相加,进而代表每个关系的embedding。每个图像的最小单位,也就是pjk的关系的embedding确认之后,就开始设计如果根据这些信息进行embeder的训练,训练embeder的时候可以使用图像的视觉关系标签,进一步扩展每个图像的fi,每个图像可以构造satisfied assignments以及unsatisfied assignments,每个图像具体构造多少需要看论文给出的代码,应该属于一个超参数调节。训练的时候是与F也就是前面介绍的所有图像的Fi的合取后的命题公式进行比较,计算距离。训练embeder的时候也是根据每个图像每个图像进行训练,只不过embeder的训练是带视觉关系标签训练的,而预测模型的视觉关系是预测得到的,仅此而已,embeder中计算距离,F其实指的就是图像I确定的公式Fi,Fi和其余assignments的距离,Fi是什么呢?Fi就是命题公式,可以理解为就是一个陈述句。我猜测,代码中就是Fi的命题的陈述句一个规范,其他的assignments是在此基础上修改,比如 exist(person) exist(car) in(person,car) drive(person,car)这个是Fi的结构,其余的unsatisfied结构可以变为 exist(person) exist(car) out(person,car) not_drive(person,car),让这些assignments与命题本身远离,由每个命题确定的Fi其实也可以看做是一个命题的satisfied assignments,只不过说这里他既可以看做命题 也可以看做assignments,不矛盾,目的都是用于未来的推理,每一个图片都可以看做是对这个知识的强化过程。具体的参考代码进一步理解。
,尽管二者都可以代表一个关系,但是表达成word的形式,可以通过word embedding增强每个关系的辨识度,以及更好地表达成向量的形式。如果不这么做,对每个关系用object和predicate的one-hot编码,会导致无法扩展的问题,每次扩展都需要生成新的one-hot,并且引入one-hot的先天稀疏的缺陷问题。因此作者使用Glove对每个关系进行embedding,然后将每个关系中的word的embedding相加,进而代表每个关系的embedding。每个图像的最小单位,也就是pjk的关系的embedding确认之后,就开始设计如果根据这些信息进行embeder的训练,训练embeder的时候可以使用图像的视觉关系标签,进一步扩展每个图像的fi,每个图像可以构造satisfied assignments以及unsatisfied assignments,每个图像具体构造多少需要看论文给出的代码,应该属于一个超参数调节。训练的时候是与F也就是前面介绍的所有图像的Fi的合取后的命题公式进行比较,计算距离。训练embeder的时候也是根据每个图像每个图像进行训练,只不过embeder的训练是带视觉关系标签训练的,而预测模型的视觉关系是预测得到的,仅此而已,embeder中计算距离,F其实指的就是图像I确定的公式Fi,Fi和其余assignments的距离,Fi是什么呢?Fi就是命题公式,可以理解为就是一个陈述句。我猜测,代码中就是Fi的命题的陈述句一个规范,其他的assignments是在此基础上修改,比如 exist(person) exist(car) in(person,car) drive(person,car)这个是Fi的结构,其余的unsatisfied结构可以变为 exist(person) exist(car) out(person,car) not_drive(person,car),让这些assignments与命题本身远离,由每个命题确定的Fi其实也可以看做是一个命题的satisfied assignments,只不过说这里他既可以看做命题 也可以看做assignments,不矛盾,目的都是用于未来的推理,每一个图片都可以看做是对这个知识的强化过程。具体的参考代码进一步理解。
*****关于命题公式的思考:*****
经常会有一个思考就是,一个命题公式有析取合取等符号构成,最小的单位是由谓词和原子构成的命题,一个命题是不区分真假的,这点会很绕,举个例子:人在车里,思维的第一反应就是认为人在车里是真的,而实际上命题并不是说确定了真或假,而是只是一种陈述句,而不是一个事实,一个事实可以用一个陈述句表述,但是一个陈述句不能代表一个事实,因为命题是抽象的,给出来的陈述句也是抽象的,具体是真是假需要赋值,也就是说只有当说:人在车里是真的,那么这个命题的真假才确定,否则命题就只是命题。那可能会想,当我们说 人在车里为假的时候,是可以用 人不在车里 这一个陈述句表述的,这就根据很矛盾很绕,但是换个角度来说这也是人的思维的一个事实。捋一下,命题的来由是人们掌握了大量的不同事实之后,经过抽象,总结出来的一套规则,目的是用于未来的未知的内容的一个判断,比如人在车里,人们肯定日常是知道这个现象的,那么对于抽象成命题之后就是对于日后情况做一个铺垫,比如我们不知道在未来的某个情景下,人在车里是否满足,那么我们先按照人在车里去假设,等到真实观测到之后确定这个假设是否成立,成立之后就会得到具有事实的描述,比如xxxx命题为真,或为假,这里也就是assignments的意思了。 总结:不要试图去解释,没有办法解释的问题,比如人为什么能够意识到 眼前石头的存在,并且进而能意识到如果不存在石头怎么办,前者的存在,是客观事实,后者的不存在虽然能思考,但是无意义,无法解释,正是由于后者的思考,带来了我们的推理能力,那么为什么我们感受到自身的推理能力呢?这也是无法解释的,但是是能够切身感受到的。命题逻辑的提出也是遵循思维和推理的一个客观产物,有观测得到命题公式,命题公式又为未来的推理提供形式化的保证。