函数原型
tf.keras.layers.Dense(units, # 正整数,输出空间的维数activation=None, # 激活函数,不指定则没有use_bias=True, # 布尔值,是否使用偏移向量kernel_initializer='glorot_uniform', # 核权重矩阵的初始值设定项bias_initializer='zeros', # 偏差向量的初始值设定项kernel_regularizer=None, # 正则化函数应用于核权矩阵bias_regularizer=None, # 应用于偏差向量的正则化函数activity_regularizer=None, # Regularizer function applied to the output of the layer (its "activation")kernel_constraint=None, # Constraint function applied to the kernel weights matrix.bias_constraint=None, **kwargs # Constraint function applied to the bias vector
)
官方地址:tf.keras.layers.Dense()
全连接层作用
全连接层在整个网络卷积神经网络中起到“特征提取器”的作用。如果说卷积层、池化层和激活函数等操作是将原始数据映射到隐层特征空间的话,全连接层则起到将学到的特征表示映射到样本的标记空间的作用。
一段来自知乎的通俗理解:
从卷积网络谈起,卷积网络在形式上有一点点像咱们正在召开的“人民代表大会”。卷积核的个数相当于候选人,图像中不同的特征会激活不同的“候选人”(卷积核)。池化层(仅指最大池化)起着类似于“合票”的作用,不同特征在对不同的“候选人”有着各自的喜好。
全连接相当于是“代表普选”。所有被各个区域选出的代表,对最终结果进行“投票”,全连接保证了receiptive field 是整个图像,既图像中各个部分(所谓所有代表),都有对最终结果影响的权利。
全连接层原理
在卷积神经网络的最后,往往会出现一两层全连接层,全连接一般会把卷积输出的二维特征图转化成一维的一个向量,这是怎么来的呢?目的何在呢?
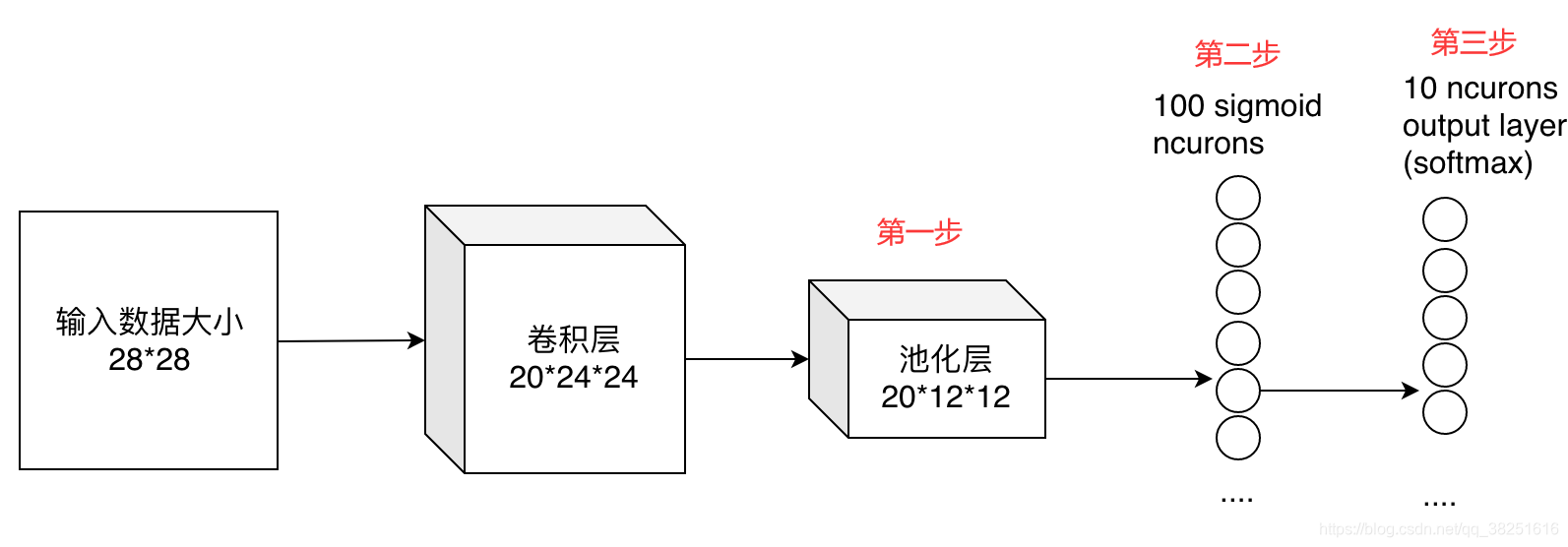
最后的两列小圆球就是两个全连接层的输出,在最后一层卷积结束后,进行了最后一次池化,得到20个12*12的图像,经过全连接层变成了1*100的向量,再次经过一次全连接层变成的1*10的向量输出。
从第一步是如何到达第三步的呢,其实就是有20*100个12*12的不同卷积核卷积出来的,我们也可以这样想,就是每个神经元的输出是12*12*20个输入值与对应的权值乘积的和。对于输入的每一张图,用了一个和图像一样大小的核卷积,这样整幅图就变成了一个数了,如果厚度是20就是那20个核卷积完了之后相加求和。这样就能把一张图高度浓缩成一个数了。
代码实例
这里以mnist数字识别中构建的模型为例,完整代码可看这里:【深度学习-卷积神经网络(CNN)实现mnist数字识别】
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu')) model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10))model.summary()
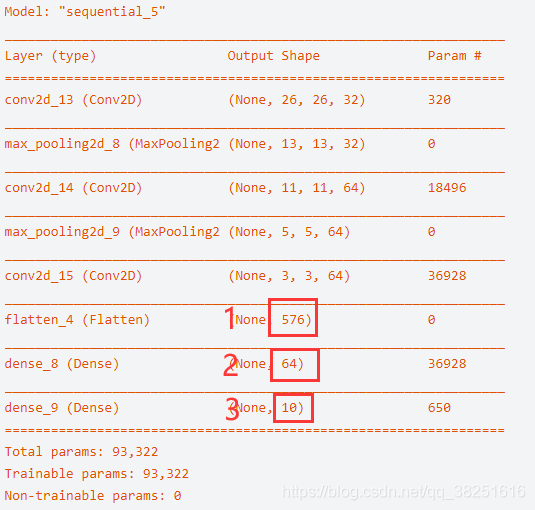
经过Flatten层后得到一个1*576的向量,经过两层的全连接层后得到1*10的向量,分别对应数字1~10。