Object detection Evaluation：mAP --- 目标检测的评测指标详解

A. 鉴别正确的检测结果并计算precision和recall
为了计算precision和recall，与所有机器学习问题一样，我们必须鉴别出True Positives（真正例）、False Positives（假正例）、True Negatives（真负例）和 False Negatives（假负例）。

为了获得True Positives and False Positives，我们需要使用IoU。计算IoU，我们从而确定一个检测结果（Positive）是正确的（True）还是错误的（False）。最常用的阈值是0.5，即如果IoU> 0.5，则认为它是True Positive，否则认为是False Positive。而COCO数据集的评估指标建议对不同的IoU阈值进行计算，但为简单起见，我们这里仅讨论一个阈值0.5，这是PASCAL VOC数据集所用的指标。

为了计算Recall，我们需要Negatives的数量。由于图片中我们没有预测到物体的每个部分都被视为Negative，因此计算True Negatives比较难办。但是我们可以只计算False Negatives，即我们模型所漏检的物体。

另外一个需要考虑的因素是模型所给出的各个检测结果的置信度。通过改变置信度阈值，我们可以改变一个预测框是Positive还是 Negative，即改变预测值的正负性(不是box的真实正负性，是预测正负性)。基本上，阈值以上的所有预测（Box + Class）都被认为是Positives，并且低于该值的都是Negatives。

对于每一个图片，ground truth数据会给出该图片中各个类别的实际物体数量。我们可以计算每个Positive预测框与ground truth的IoU值，并取最大的IoU值，认为该预测框检测到了那个IoU最大的ground truth。然后根据IoU阈值，我们可以计算出一张图片中各个类别的正确检测值（True Positives, TP）数量以及错误检测值数量（False Positives, FP）。据此，可以计算出各个类别的precision：

既然我们已经得到了正确的预测值数量（True Positives），也很容易计算出漏检的物体数（False Negatives, FN）。据此可以计算出Recall（其实分母可以用ground truth总数）：

B. 计算mAP

mAP这个术语有不同的定义。此度量指标通常用于信息检索和目标检测领域。然而这两个领域计算mAP的方式却不相同。这里我们只谈论目标检测中的mAP计算方法。

在目标检测中，mAP的定义首先出现在PASCAL Visual Objects Classes(VOC)竞赛中，这个大赛包含许多图像处理任务，详情可以参考这个paper（里面包含各个比赛的介绍以及评估等）。

前面我们已经讲述了如何计算Precision和Recall，但是，正如前面所述，至少有两个变量会影响Precision和Recall，即IoU和置信度阈值。IoU是一个简单的几何度量，可以很容易标准化，比如在PASCAL VOC竞赛中采用的IoU阈值为0.5，而COCO竞赛中在计算mAP较复杂，其计算了一系列IoU阈值（0.05至0.95）下的mAP。但是置信度却在不同模型会差异较大，可能在我的模型中置信度采用0.5却等价于在其它模型中采用0.8置信度，这会导致precision-recall曲线变化。为此，PASCAL VOC组织者想到了一种方法来解决这个问题，即要采用一种可以用于任何模型的评估指标。在paper中，他们推荐使用如下方式计算Average Precision（AP）：

For a given task and class, the precision/recall curve is computed from a method’s ranked output. Recall is defined as the proportion of all positive examples ranked above a given rank. Precision is the proportion of all examples above that rank which are from the positive class. The AP summarises the shape of the precision/recall curve, and is defined as the mean precision at a set of eleven equally spaced recall levels [0,0.1,…,1]:

可以看到，为了得到precision-recall曲线，首先要对模型预测结果进行排序（ranked output，按照各个预测值置信度降序排列）。那么给定一个rank，Recall和Precision仅在高于该rank值的预测结果中计算，改变rank值会改变recall值。这里共选择11个不同的recall（[0, 0.1, …, 0.9, 1.0]），可以认为是选择了11个rank，由于按照置信度排序，所以实际上等于选择了11个不同的置信度阈值。那么，AP就定义为在这11个recall下precision的平均值，其可以表征整个precision-recall曲线（曲线下面积）（我来解释一下，要得到Precision-Recall曲线(以下简称PR)曲线，首先要对检测模型的预测结果按照目标置信度降序排列。然后给定一个rank值，Recall和Precision仅在置信度高于该rank值的预测结果中计算，改变rank值会相应的改变Recall值和Precision值。这里选择了11个不同的rank值，也就得到了11组Precision和Recall值，然后AP值即定义为在这11个Recall下Precision值的平均值，其可以表征整个PR曲线下方的面积）。

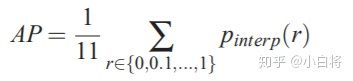
另外，在计算precision时采用一种插值方法（interpolate）：

The precision at each recall level r is interpolated by taking the maximum precision measured for a method for which the corresponding recall exceeds r:
The intention in interpolating the precision/recall curve in this way is to reduce the impact of the “wiggles” in the precision/recall curve, caused by small variations in the ranking of examples.

及对于某个recall值r，precision值取所有recall>=r中的最大值（这样保证了p-r曲线是单调递减的，避免曲线出现摇摆）:

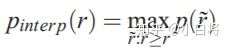
不过这里VOC数据集在2007年提出的mAP计算方法，而在2010之后却使用了所有数据点，而不是仅使用11个recall值来计算AP（详细参考这篇paper）：

Up until 2009 interpolated average precision (Salton and Mcgill 1986) was used to evaluate both classification and detection. However, from 2010 onwards the method of computing AP changed to use all data points rather than TREC-style sampling (which only sampled the monotonically decreasing curve at a fixed set of uniformly-spaced recall values 0, 0.1, 0.2,…, 1). The intention in interpolating the precision–recall curve was to reduce the impact of the ‘wiggles’ in the precision–recall curve, caused by small variations in the ranking of examples. However, the downside of this interpolation was that the evaluation was too crude to discriminate between the methods at low AP.

对于各个类别，分别按照上述方式计算AP，取所有类别的AP平均值就是mAP。这就是在目标检测问题中mAP的计算方法。可能有时会发生些许变化，如COCO数据集采用的计算方式更严格，其计算了不同IoU阈值和物体大小下的AP（详情参考COCO Detection Evaluation）。

当比较mAP值，记住以下要点：

1. mAP通常是在一个数据集上计算得到的。
2. 虽然解释模型输出的绝对量化并不容易，但mAP作为一个相对较好的度量指标可以帮助我们。 当我们在流行的公共数据集上计算这个度量时，该度量可以很容易地用来比较目标检测问题的新旧方法。
3. 根据训练数据中各个类的分布情况，mAP值可能在某些类（具有良好的训练数据）非常高，而其他类（具有较少/不良数据）却比较低。所以你的mAP可能是中等的，但是你的模型可能对某些类非常好，对某些类非常不好。因此，建议在分析模型结果时查看各个类的AP值。这些值也许暗示你需要添加更多的训练样本。

C. PR曲线
我们当然希望检测的结果P越高越好，R也越高越好，但事实上这两者在某些情况下是矛盾的。比如极端情况下，我们只检测出了一个结果，且是准确的，那么Precision就是100%，但是Recall就很低；而如果我们把所有结果都返回，那么必然Recall必然很大，但是Precision很低。

因此在不同的场合中需要自己判断希望P比较高还是R比较高。如果是做实验研究，可以绘制Precision-Recall曲线来帮助分析。

这里我们举一个简单的例子，假设我们的数据集中共有五个待检测的物体，我们的模型给出了10个候选框，我们按照模型给出的置信度由高到低对候选框进行排序。

表格第二列表示该候选框是否预测正确（即是否存在某个待检测的物体与该候选框的iou值大于0.5）第三列和第四列表示以该行所在候选框置信度为阈值时，Precision和Recall的值。我们以表格的第三行为例进行计算：

由上表以Recall值为横轴，Precision值为纵轴，我们就可以得到PR曲线。我们会发现，Precision与Recall的值呈现负相关，在局部区域会上下波动。

D. AP(Average Precision)
顾名思义AP就是平均精准度，简单来说就是对PR曲线上的Precision值求均值。对于pr曲线来说，我们使用积分来进行计算。

在实际应用中，我们并不直接对该PR曲线进行计算，而是对PR曲线进行平滑处理。即对PR曲线上的每个点，Precision的值取该点右侧最大的Precision的值。


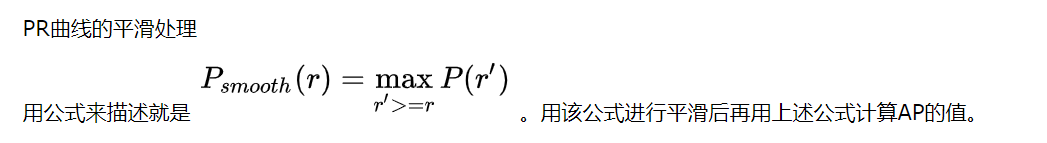
E. Interplolated AP（Pascal Voc 2008 的AP计算方式）
Pascal VOC 2008中设置IoU的阈值为0.5，如果一个目标被重复检测，则置信度最高的为正样本，另一个为负样本。在平滑处理的PR曲线上，取横轴0-1的10等分点（包括断点共11个点）的Precision的值，计算其平均值为最终AP的值。

F. Area under curve
上述方法有两个缺陷，第一个是使用11个采样点在精度方面会有损失。第二个是，在比较两个AP值较小的模型时，很难体现出两者的差别。所以这种方法在2009年的Pascalvoc之后便不再采用了。在Pascal voc 2010之后，便开始采用这种精度更高的方式。绘制出平滑后的PR曲线后，用积分的方式计算平滑曲线下方的面积作为最终的AP值。

参考链接

1. https://zhuanlan.zhihu.com/p/37910324
2. https://www.cnblogs.com/hanhao970620/p/12422473.html