双目立体视觉笔记（三）三角测量、极线校正

三角测量和极线校正

·三角测量

假设两个相机像平面精准位于同一平面上，且行对齐，两个光轴严格平行。

利用三角形关系，我们不难推出Z值：

如果主点$c_x^l$，$c_x^r$坐标相同则可简化为：

因为视差$d=x^l?x^r$，且$Z$为我们的深度值$depth$，故：
$depth=\frac{fT}{d}$

·视差与深度图关系

（1）视差与深度成反比，视差接近0时，微小的视差变化会产生较大的深度变化。
（2）当视差较大时，微小的视差变化几乎不会引起深度多大的变化。
（3）因此，立体视觉系统仅物体距离相机较近时具有较高的深度精度。

·极线校正

（1）校正的过程：就是将相机在数学上对准到同一观察平面上，使得相机像素行是严格对齐的。
（2）校正的目的：对两幅图像的二维匹配搜索变成一维，节省计算量，排除虚假匹配点。

·校正算法

为了将相机极点变换到无穷远使得极线水平对准，我们创建一个旋转矩阵，首先是$X$轴的旋转，我们将$X$轴旋转到与基线相同的方向即旋转后新$X$轴就是$O_l?O_r$，旋转向量：$e_1=\frac{T}{|T|}$。

确定旋转后的新$Y$轴，只需满足与$e_1$正交即可：选择与主光轴和$e_1$相交的方向：
$e_2=e_1\times (R_l[0,0,1{]}^T+t_l)$

新的$Z$轴，与$e_1,e_2$垂直且满足右手法则：$e_3=e_1\times e_2$，

最终得到的旋转矩阵：$R_{new}=[e_1,e_2,e_3]$，

新的旋转矩阵：$R_l^{new}=R_{new}{R}_l^t$，$R_r^{new}{R}_{new}{R}_r^t$,

校正后，baseline $T$计算：

下式中$c_{lr}$是指右相机光心在左相机坐标系下的坐标（也等于与右相机光心[0,0,0]的距离）， t求解公式的意义是左相机光心在右相机校正后的坐标系下的坐标（也等于与右相机校正后的坐标系下光心[0,0,0]的距离）。故baseline就是x轴方向的距离。

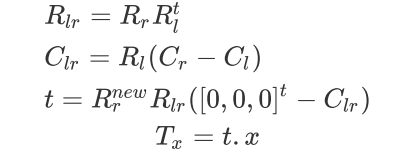
·视差图转深度图

视差图是校正后的坐标系下得到的值,首先将其转换为校正后坐标系下的深度图
已知：

则：

把上式写成矩阵形式：

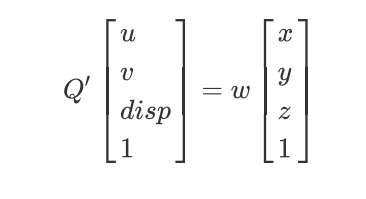
式中$Q^{{}^{\prime }},w$定义如下：

将校正后的坐标系下深度图转换到校正前的相机坐标系下
已知：校正前的相机坐标系下坐标$(x,y,z)$转到校正后相机坐标系下坐标$(x^{{}^{\prime }},y^{{}^{\prime }},z^{{}^{\prime }})$转换关系如下：

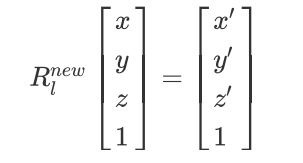
则已知校正后的求校正前的公式如下:

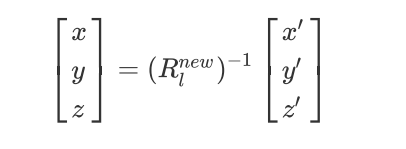
再将其投影到图像坐标系下：

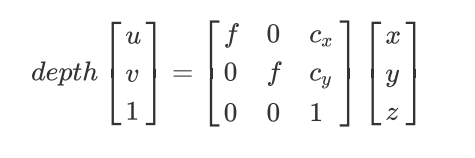
即：

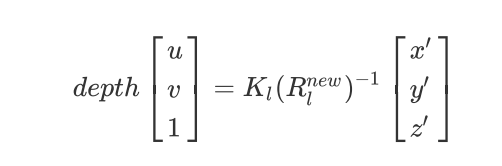
将上两步合并得到校正后坐标系下的视差图$(u^{{}^{\prime }},v^{{}^{\prime }},disp)$ 与校正前的坐标系下的深度图$(u,v,depth)$的转换矩阵$Q$，已知：

则：

·立体匹配

三维重建的核心就是立体匹配。通过寻找匹配点，利用三角测量或对极约束得到其在空间中的3D信息。

立体匹配算法主要分为全局、局部、半全局。

（1）全局立体匹配算法：
全局立体匹配算法主要是采用了全局的优化理论方法估计视差，建立全局能量函数，通过最小化全局能量函数得到最优视差值。通过二维相邻像素视差之间的约束（如平滑性约束）而得到更好的匹配效果，但是对内存的占用量大，速度慢不适合实时运行。主要的算法有图割（graph cuts）、信念传播（belief propagation）、动态规划等算法。

（2）局部立体匹配算法：
主要是采用局部优化方法进行视差值估计，局部立体匹配算法有 SAD，SSD 等算法，与全局立体匹配
算法一样，也是通过能量最小化方法进行视差估计，但是在能量函数中，只有数据项，而没有平滑项。
该算法由于每个像素计算互不干扰可以并行计算，所以可以实时。但由于所基于的局部窗口视差相同的
假设在很多情况下并不成立导致匹配效果较差。

（3）半全局立体匹配算法SGM
综合上述局部和全局算法的优缺点，半全局算法依旧采用全局框架，但是在计算能量函数最小化的步骤
时使用高效率的一维路径聚合方法来代替全局算法中的二维最小化算法，使用一维最优来近似二维最优，得到的视差图在效果上和全局算法没有太大的差别，但是算法效率却有非常大的提升。