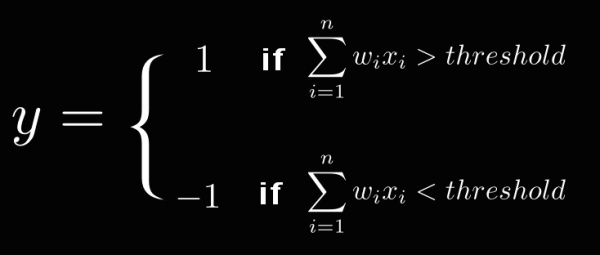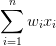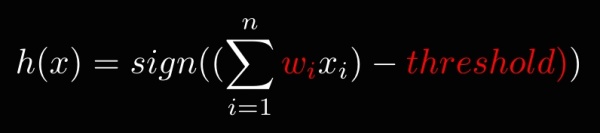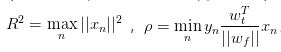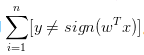作者:徐晗曦
原文:写给大家看的机器学习书(第三篇)
本次转载已获得作者授权,尊重原创,若需转载请联系作者本人。相关文章:
写给大家看的机器学习书【Part1】什么是机器学习?机器学到的到底是什么?
写给大家看的机器学习书【Part2】训练数据长什么样?机器学到的模型是什么?这个系列文章,我将试着为开发工程师,产品经理、设计师、所有希望了解学习机器学习的人,介绍机器学习的原理、方法和实战技巧。
本篇综述
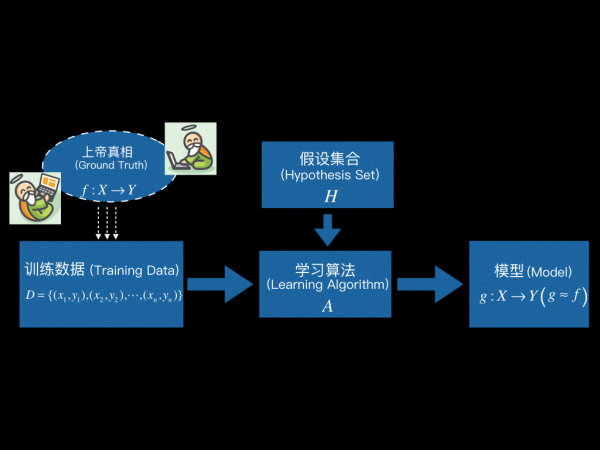
前两篇我们已经学习了机器学习的概念和组成:
学习算法 (Learning Algorithm) 根据训练数据,从假设集合 (Hypothesis Set) 中选出最优的那个映射g : χ → Y 作为最终学得的模型,使得 g 越接近 f 越好( g ≈ f )。
这一篇,我们要具体地讲一个学习算法,把它用在有好货这个场景,看看这个算法到底是怎么样从用户日志中寻找规律,学得模型的。一旦学得模型以后就可以对未来做出预测 —— 预测用户是否会点击某个商品,预测人生的巅峰、世界的和平、一起学习机器学习的女朋友…
这个学习算法的名字叫 PLA,全称 Perceptron Learning Algorithm。其中 Perceptron 译作感知机,它是人工神经网络中最基础的两层神经网络模型。学好Perceptron Learning Algorithm,你离入门人工神经网络也就不远啦。
具体来说,这一篇我们将首先介绍PLA的假设集合,看看PLA的假设集合中等着被挑选的候选函数长什么样。看过PLA假设集合的函数表示之后,重要的是理解PLA假设集合的直观解释,事实上之所以把PLA作为第一个学习算法,就是因为它有着非常直观的理解方式。
接着将看到PLA的细节,PLA 是一个相当简洁的算法,算法过程仅有4步,我写的Python 编码含注释不到30行。学习PLA的重点应该放在理解PLA算法的第三步,理解PLA之所以被设计成这样,背后的含义其实朴素又直观。
然后,我们将讨论学习算法两个很重要的问题——学习算法能最终停止并学到东西吗?如果能,学习算法需要运行多久呢?这时我们将惊讶于经典PLA的两点性质:(1)算法可能永远也无法运行结束,会迷失在茫茫的训练数据中永远找不到出口。(2)哪怕知道PLA最终能找到出口,我们也无法事先知道学习需要花多久。不过别急于换台,我们紧接着就会给出一版升级的PLA算法,只需在经典PLA的基础上增加简单两步,就可以解决上面的问题。
好,我们开始吧。
1. PLA 的假设集合 (Hypothesis Set)
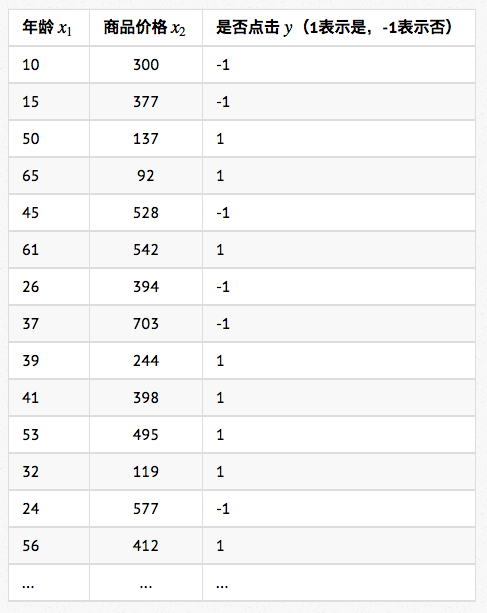
首先,我们从有好货的用户日志中得到训练数据如下(考虑数据安全,数据当然是我Mock的):
如第二篇第2小节所述,每一条样本表示为x = (x1, x2),其中x1表示年龄,x2表示商品价格。样本标注用y表示,y=1表示用户点击,y=-1表示用户没点击。(这里我们只选了年龄和商品价格两个维度的特征,当然是为了方便讲解和作图做得简化,实际应用中会使用到多得多的特征)
PLA 的基本想法是每个特征都有个权重wi ,表示该特征的重要程度。综合所有的特征和权重计算一个最终的分数,如果分数超过某个阈值 (threshold ),就表示用户会点击,否则则不会点击。
我们将特征的权重记作w=(w1,w2),w1代表了年龄这维特征的重要性,w2代表了商品价格这维特征的重要性。于是判断一个用户会不会点击,就变成了下面这个函数:
如果
大于threshold ,那么我们判断用户会点击。
如果
小于threshold,我们判断用户不会点击。
该函数经过简单变换,可以表示得更简洁。如下所示,其中sign(x) 是求表达式的符号,当x大于0时,sign(x) 就等于1。当x小于0时,sign(x) 就等于-1:
注意,在算法完成学习之前,函数中的wi和threshold 是未知的,不同的wi和threshold 值对应了不同的函数,事实上所有可能的wi和threshold 所代表的函数集合,构成了PLA的假设集合(Hypothesis Set),叫做 Perceptron Hypothesis 。而 PLA 算法要做的,就是根据训练数据找到最优的w和threshold 。
2. Perceptron Hypothesis 的直观解释
OK,上小节我们知道了 PLA 的假设集合 (Hypothesis Set) 就是所有可能的h(x),不过函数表示理解起来还是有点抽象,那么 Perceptron Hypothesis 有没有直观的理解方式呢?有!
在有好货的例子里,x=(x1,x2)只有两维特征,于是我们先将函数简化:
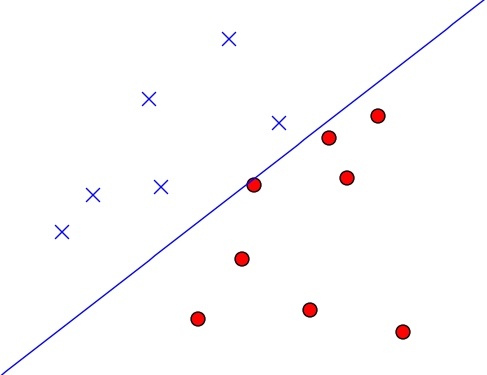
接着把所有训练样本x=(x1,x2)画到二维平面上,红圈表示点击,蓝叉表示没点击,如下图所示:
由于方程w1·x1 + w2·x2 - threshold = 0就表示平面上的一条直线,且我们知道直线右边所有的点都有w1·x1 + w2·x2 - threshold > 0,左边所有的点都有w1·x1 + w2·x2 - threshold < 0 , 于是可以推出:
PLA假设集合中任意一个确定的h(x) ,都可视作一条直线将平面分隔成了两个区域。线的左边有h(x) = -1,右边有h(x) = 1。
所以,学习算法希望选中的模型g ,就是如上图所示这样的一条线,它正好将训练数据分成两个区域,右边都是红圈,左边都是蓝叉。也正因为这样,Perceptron 是一种线性分类器(Linear Classifiers)。
3. PLA 怎么选一条最好的线
直观理解了 PLA 的 Hypothesis Set 之后,现在我们来看看 PLA 具体是如何确定最优的w和threshold ,得到最优的那条线的。
我们首先需要对公式做一些简化变形:
这个变形的目的是把参数threshold 统一收进w,于是 PLA 找到最优的那条线就等价于找到最优的参数w。于是 PLA 算法就可以写得相当简洁,仅有如下4步:
- Step 1: 随便找一条线,即任意找一个 n 维向量w0,赋初值令w = w0
- Step 2: 如果这条线正好把训练数据正确切分,Lucky!!训练结束!!此时w代表的h(x) 就是我们学得的模型g
- Step 3: 如果有任意一个样本没有被切分正确,即存在任意(x’, y’),使得sign( wT x’) ≠ y’,此时我们对w代表的线做一点点修正,令wt+1 = wt + y’x’
- Step 4: 跳转到Step 2
就是这么简单,PLA的基本思路就是:先随便找一条线,如果没能正确切分,就修正一点点,直到所有的红圈都在右边,蓝叉都在左边。
Python 编码含注释不到30行(包含画图展示的完整代码可访问我的 Github):
import numpy as np
import matplotlib.pyplot as pltdef PLA(trainingData):w = np.mat([1,2127,205]).transpose() # Step 1: 向量w赋初值while True: (status, x, y) = noMistakePoint(trainingData, w)if status == 'YES': # Step 2: 切分正确,学习完成return welse:w = w + y*x # Step 3: 修正wdef noMistakePoint(training_data, w):'''训练数据中是否有点被切分错误'''status = 'YES'for (x, y) in training_data:if mSign(w.transpose() * x) <> sign(y):status = 'NO'return (status, x, y)return status, None, Nonesign = lambda x:1 if x > 0 else -1 if x < 0 else -1
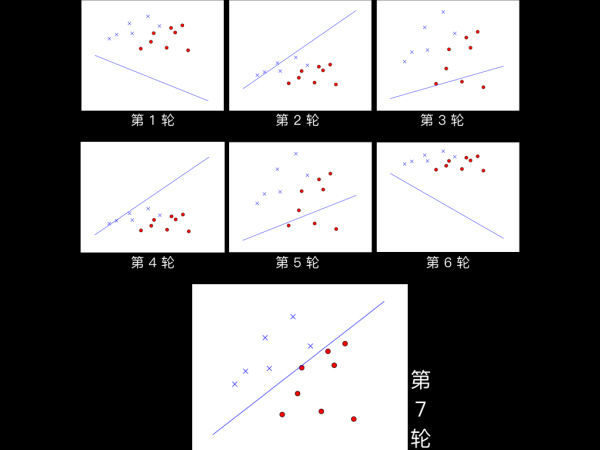
def mSign(m):'''判断某个矩阵的[0][0]元素正负.大于0返回1,否则返回-1'''x = m.tolist()[0][0]return 1 if x > 0 else -1 if x < 0 else -1每对训练数据进行一次循环遍历我们称为“一轮学习”,当w的初值设为w0=( 1,2127,205 )时,PLA仅需 7 轮就成功找到了能够正确切分训练数据的线(如下图所示),最终PLA得到的w=( -1, 2169, -216 ),即学得的模型为g(x) = sign ( 2169 · x1 - 216 · x2 -1)。
PLA 算法很简单,学习的关键在于理解算法的第3步,怎么理解当发现一个样本(x’, y’)没被切分正确时,对 w 的修正是wt+1 = wt + y’x’呢?这个修正的含义是什么呢?
分两种情况来分析:
情况1:被错分的点是红圈。也就是说y’是+1,sign(wT x’)却等于-1,使得sign(wT x’) ≠ y’。学过向量乘的同学都知道,两个向量wT和x’相乘小于0,说明它们的夹角大于90°。如果希望它们相乘大于0,需要把夹角变小,而另w = w + y’x’(即w = w + x’)之后正是另两个向量的夹角变小了——如下图情况1所示。
情况2同理:被错分的点是蓝叉。也就是说y’是-1,sign( wT x’)却等于+1,使得sign( wT x’) ≠ y’。说明 wT和x’的夹角小于90°,如果希望它们相乘小于0,需要把夹角变大,而另w = w+y’x’(即 w = w - x’)之后正是另两个向量的夹角变大了——如下图情况2所示。
这就是每次修正直线背后的含义。
4. PLA 一定会停吗?PLA 多久会停?
当 PLA 停止计算时,就说明它找到了一条线能将所有的训练数据切分正确。那么问题来了,PLA 一定会停吗?它一定能找到这样的一条直线吗?
答案是:不一定!
事实上,如果训练数据本身就不存在任何一条线能将其正确切分,比如如下图所示,那么 PLA 无论如何也无法找到理想的直线。学习将进入永不停止的循环。
训练数据至少存在一条直线能将其切分开,称为训练数据是线性可分的 (Linear Seperable) 。因此:
训练数据是线性可分的 (Liner Seperable) ,是 PLA 能够学习的必要条件。
好,如果假设训练数据是线性可分的,PLA 的计算需要多久才能停呢?这里省略具体推导过程(有兴趣可观看机器学习基石课程的推导),推导可得 PLA 最多需要R2 / ρ2轮就会停,其中
注意ρ的公式中用到了“上帝真相”f,而f是未知的,这就意味着哪怕我们知道PLA在线性可分的训练数据上会停止,但具体多久会停止这个值无法计算出来 :(
5. PLA 搞鸡毛啊!
这个时候有的朋友要骂娘啦,整了半天 PLA 的训练数据必须线性可分,哪怕线性可分需要计算多久也不知道。PLA 搞鸡毛啊!
不要急!!大招马上出来。
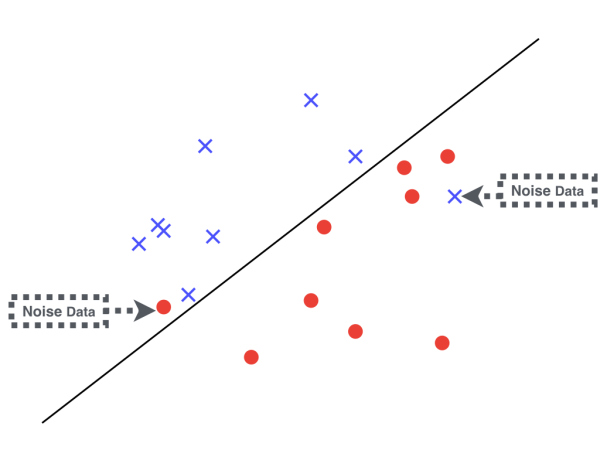
我们再看看下面这张图,这里的训练数据不是线性可分,是由其中两个点导致的。在现实中,哪怕原本的训练数据产生于某个“上帝真相”并且是线性可分的,在收集数据处理数据的过程中不可避免的会引入一些脏数据,这部分错误的训练数据我们称为噪声(Noise)。针对这种噪声数据引起的,原本线性可分的训练数据变成了不是线性可分的情况,有一个升级版的 PLA 算法,只需要增加简单的两步节能解决问题:
- Step 1: 随便找一条线,即任意找一个 n 维向量w0,赋初值另w0。同时用一个变量wbest表示在训练数据上表现最好的线,初始有wbest= w0。
- Step 2: 如果这条线正好把训练数据正确切分,Lucky!! 训练结束!!此时w代表的h(x) 就是我们学得的模型g 。
- Step 3: 如果有任意一个样本没有被切分正确,即存在任意(x’, y’),使得sign(wT x’) ≠ y’,此时我们对w代表的线做一点点修正,令wt+1 = wt + y’x’ 。
- Step 4: 如果修正后的wt+1比wbest表现的更好,那么修改wbest = wt+1。
- Step 5: 如果训练轮数小于Ntrain,跳转到Step 2。否则训练结束,此时wbest代表的h(x)就是我们学得的模型g。
升级版的 PLA 算法来自于实际经验,当噪声较小时,经过一定次数的训练之后并把表现最好的线记下来,也能得到一个不错解。上面说wt+1和wbest表现的好坏,是指这条线在训练数据上犯了多少错,即
至此,升级版的 PLA 算法无需要求训练数据线性可分,训练最多也会在Ntrain轮内结束。:)
试试动手写写看升级版的 PLA 算法吧。
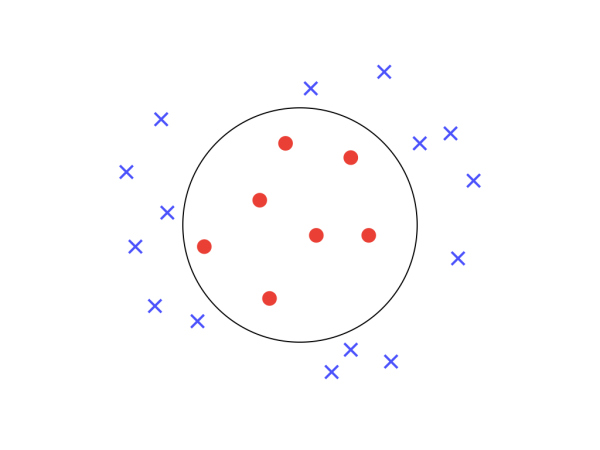
当然,如果你的训练数据不是线性可分是下图这种情况,作为线性分类器的 PLA 是无能为力的,这需要后面要讲的非线性模型来搞定。期待一下吧。
预告和其它
下一篇我们将围绕一个有关赚钱的机器学习问题展开讨论。
你是否也有过那么一时三刻的不自信:当你有一天成了机器学习专家,学会了从股市的历史数据中学得模型,这个时候你敢跟着模型对股市的预测,进行真金白银的投资吗?
所谓“有史为鉴,可以知兴亡”,从历史中总结出的规律,真的能在未来的预测中被信赖吗?为了做一个对未来负责的机器学习专家,我们下一篇将展开对这个问题的讨论。
感谢您的阅读,如果你希望收到后续文章的更新,可以考虑关注我。或者关注这个同名专栏,文章将会在您的通知中心推送更新。
再次感谢您的阅读,这里是《写给大家看的机器学习书》,希望我有把事情说清楚,有任何疑惑或者问题,欢迎留言。
祝开心 :)
下一篇:写给大家看的机器学习书(Part4)—— 机器学习为什么是可行的(上)