仿真的条件与之前讲解非线性算法之牛顿——拉夫森算法时候的仿真条件一致。从下面的定位示意图中也能看出来,测量站的位置以及个数,以及目标位置。
测量站的位置:x1 = [0,0];x2 = [0,10];x3 = [10,0];x4 = [10,10];
目标的真实位置:x=[2,3].
信噪比正常定义,设定为30dB,从下图的定位示意图中可以看出,基本可以定位,因为估计出来的目标位置与目标真实位置基本重合,但存在一定的误差。这就要求我们去分析误差,看看什么样的误差我们能够接受,对应的信噪比是多少?

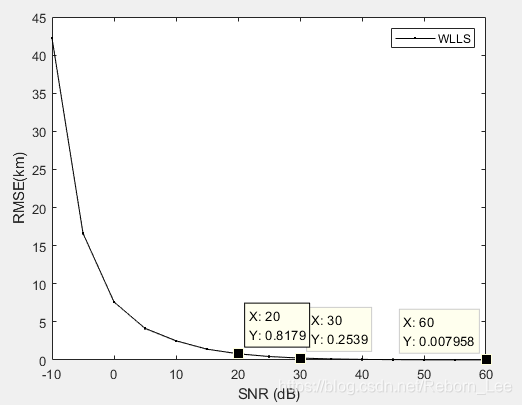
从下图的定位误差分析图中可以看出,信噪比为20dB时候的定位误差达到了817m,信噪比为30dB时候的定位误差为253m,这与之前的非线性方法相比,定位误差不相上下,但是与lls方法相比,定位误差小了一些,说明WLLS算法确实定位准确呀。
为了方便使用,可以将WLLS算法编写成一个函数:
function x = wlls(X,r,sigma2)
% WLLS algorithm
% --------------------------------
% x = wlls(X,r,sigma2);
% x = 2D position estimate
% X = matrix for receiver positions
% r = TOA measurement vector
% sigma2 = noise variance vector
% L = size(X,2); % number of receivers
A = [-2*X' ones(L,1)];
b = r.^2-sum(X'.^2,2);
W = 1/4*diag(1./(sigma2.*r.^2));
p = pinv(A'*W*A)*A'*W*b;
x= [p(1) ; p(2)];