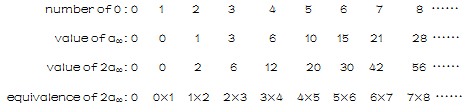Codeforces Problem 708B Recover the String

Accept: 0 Submit: 0
Time Limit: 1 second Memory Limit : 256 megabytes

Problem Description

For each string s consisting of characters '0' and '1' one can define four integers a00, a01, a10 and a11, where axy is the number of subsequences of length 2 of the string s equal to the sequence {x,?y}.

In these problem you are given four integers a00, a01, a10, a11 and have to find any non-empty string s that matches them, or determine that there is no such string. One can prove that if at least one answer exists, there exists an answer of length no more than 1?000?000.

Input

The only line of the input contains four non-negative integers a00, a01, a10 and a11. Each of them doesn't exceed 10^9.

Output

If there exists a non-empty string that matches four integers from the input, print it in the only line of the output. Otherwise, print "Impossible". The length of your answer must not exceed 1?000?000.

Sample Input

2 3 4 
   
2 2 1

Sample Output

   Impossible 
   
 0110

Hint

Problem Idea

解题思路:

【题意】
给你4个整数,a00,a01,a10,a11,分别表示01字符串s中子序列为{0,0},{0,1},{1,0},{1,1}的个数

问字符串s为多少,若不存在这样的字符串,则输出"Impossible"

【类型】
数学

【分析】

因为a00表示字符串s中子序列为{0,0}的个数,那么,我们可以通过a00来求得字符串s中0的个数

由此,我们便可计算出字符串s中0的个数,记做l

同理,字符串s中1的个数也可以通过a11求得,方法同上,1的个数记做r

在字符串s中,1的个数和0的个数都确定的情况下,子序列{1,0}和子序列{0,1}的总个数也是确定的

因为对于每个0来说,任何一个1要么在它左边,构成子序列{1,0};要么在它右边,构成子序列{0,1}

故对每个0来说,子序列{1,0}和子序列{0,1}的总个数为r,那l个0则有l×r个子序列{1,0}或{0,1}

故l×r!=a01+a10时,必然不存在这样的字符串s

若字符串s已经确定存在,那我们只要考虑如何构造出a01个子序列{0,1}即可

那要如何构造呢?

对字符串s从左到右放置0,1,对于字符串s的第i个位置,若此时还有l个0和r个1未放置

那么如果我在该位置放0,那么字符串s的子序列{0,1}会增加r个,因为此时还有r个1未放,最终它们必然会放在该0的右边

如果不想要子序列{0,1}个数增加,则在该位置放1

这样操作直至凑够子序列{0,1}的个数

另外,此题需要特别注意的是,a00,a01,a10,a11是非负整数,故可能会取0

而a00,a11取值为0时,不一定指没有0或1,可能有1个0或者1个1,因为只有1个的时候,也是构不成子序列{0,0}或{1,1}的

所以这点要考虑到,之前没考虑到还错了几次

当a00=a01=a10=a11=0时,此时答案为0或1都可以

【时间复杂度&&优化】
O(√n)

题目链接→Codeforces Problem 708B Recover the String

Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 100005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
int main()
{int a00,a01,a10,a11,l,r;scanf("%d%d%d%d",&a00,&a01,&a10,&a11);l=1+(int)sqrt(2.0*a00);//字符串s中0的个数r=1+(int)sqrt(2.0*a11);//字符串s中1的个数if(a01+a10==0){l=a00?l:0;r=a11?r:0;if(a00+a11==0)l=1;//or r=1}if(l*(l-1)!=2*a00||r*(r-1)!=2*a11||a01+a10!=l*r){puts("Impossible");return 0;}while(a01){if(r>a01)printf("1"),r--;elseprintf("0"),l--,a01-=r;}while(r--)printf("1");while(l--)printf("0");puts("");return 0;
}

菜鸟成长记

Codeforces Problem 708B Recover the String(implementationmath)