此文章可以使用目录功能哟↑(点击上方[+])
比赛链接→Codeforces Round #369 (Div. 2)
Codeforces Problem 711B Chris and Magic Square
Accept: 0 Submit: 0
Time Limit: 2 seconds Memory Limit : 256 megabytes
Problem Description
ZS the Coder and Chris the Baboon arrived at the entrance of Udayland. There is a n?×?n magic grid on the entrance which is filled with integers. Chris noticed that exactly one of the cells in the grid is empty, and to enter Udayland, they need to fill a positive integer into the empty cell.
Chris tried filling in random numbers but it didn't work. ZS the Coder realizes that they need to fill in a positive integer such that the numbers in the grid form a magic square. This means that he has to fill in a positive integer so that the sum of the numbers in each row of the grid (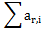
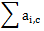
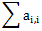
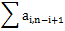
Chris doesn't know what number to fill in. Can you help Chris find the correct positive integer to fill in or determine that it is impossible?
Input
The first line of the input contains a single integer n (1?≤?n?≤?500) — the number of rows and columns of the magic grid.
n lines follow, each of them contains n integers. The j-th number in the i-th of them denotes ai,?j (1?≤?ai,?j?≤?10^9 or ai,?j?=?0), the number in the i-th row and j-th column of the magic grid. If the corresponding cell is empty, ai,?j will be equal to 0. Otherwise, ai,?j is positive.
It is guaranteed that there is exactly one pair of integers i,?j (1?≤?i,?j?≤?n) such that ai,?j?=?0.
Output
Output a single integer, the positive integer x (1?≤?x?≤?10^18) that should be filled in the empty cell so that the whole grid becomes a magic square. If such positive integer x does not exist, output ?-?1 instead.
If there are multiple solutions, you may print any of them.
Sample Input
4 0 2
3 5 7
8 1 6
4
1 1 1 1
1 1 0 1
1 1 1 1
1 1 1 1
4
1 1 1 1
1 1 0 1
1 1 2 1
1 1 1 1
Sample Output
1
-1
Hint
In the first sample case, we can fill in 9 into the empty cell to make the resulting grid a magic square. Indeed,
The sum of numbers in each row is:
4?+?9?+?2?=?3?+?5?+?7?=?8?+?1?+?6?=?15.
The sum of numbers in each column is:
4?+?3?+?8?=?9?+?5?+?1?=?2?+?7?+?6?=?15.
The sum of numbers in the two diagonals is:
4?+?5?+?6?=?2?+?5?+?8?=?15.
In the third sample case, it is impossible to fill a number in the empty square such that the resulting grid is a magic square.
Problem Idea
解题思路:
【题意】
n*n的矩阵,有一个格子还未填上数
问该格子内应该填多少,才能使得每行每列以及主副对角线之和相等
【类型】
constructive algorithms
【分析】
我们暂时先不管未填数的格子里的数应该是多少
先遍历一遍,求出当前每行元素之和r[i],每列元素之和c[i],以及主对角线元素之和d[0],副对角线元素之和d[1],并记录最大和Max
因为每个格子内填的数都是正数,所以在存在解的情况下,最大和Max必定是最终每行每列以及主副对角线之和要达到的值
这点是毋庸置疑的
那么未填数的那个格子所在行或列,元素之和与Max的差值就是该格子内应该填的数
这样我们在该格子内填入数之后,再判断一遍是否每行每列及主副对角线之和相等就可以了
当然,n=1的情况要另外考虑,因为这种情况,初始每行每列及主副对角线元素之和均为0,所以未填数的格子可以填10^18以内的任意正整数
还有要注意的一点是,若未填数的那个格子所在行或列的元素之和与Max的差值为0,这种情况也是无解的
【时间复杂度&&优化】
O(n^2)
题目链接→Codeforces Problem 711B Chris and Magic Square
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 505;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
int s[N][N];
__int64 r[N],c[N],d[2];
int main()
{int n,i,j,x,y;__int64 Max=0,k;scanf("%d",&n);for(i=0;i<n;i++)for(j=0;j<n;j++){scanf("%d",&s[i][j]);if(!s[i][j])x=i,y=j;r[i]+=s[i][j];Max=max(r[i],Max);c[j]+=s[i][j];Max=max(c[j],Max);if(i==j)d[0]+=s[i][j],Max=max(d[0],Max);if(i+j==n-1)d[1]+=s[i][j],Max=max(d[1],Max);}if(n==1){puts("1");return 0;}k=Max-r[x];r[x]=Max,c[y]+=k;if(x==y)d[0]+=k;if(x+y==n-1)d[1]+=k;for(i=0;i<n;i++)if(r[i]!=Max||c[i]!=Max)break;if(k<=0||i<n||d[0]!=Max||d[1]!=Max)puts("-1");elseprintf("%I64d\n",k);return 0;
}