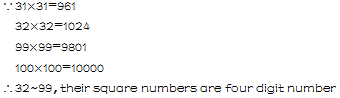此文章可以使用目录功能哟↑(点击上方[+])
CSU Problem 1785 又一道简单题
Accept: 0 Submit: 0
Time Limit: 5 Sec Memory Limit : 128 MB
Problem Description
输入一个四个数字组成的整数 n,你的任务是数一数有多少种方法,恰好修改一个数字,把它 变成一个完全平方数(不能把首位修改成 0)。比如n=7844,有两种方法:3844=62^2和 7744=88^2。
Input
输入第一行为整数 T (1<=T<=1000),即测试数据的组数,以后每行包含一个整数 n (1000<=n<=9999)。
Output
对于每组数据,输出恰好修改一个数字,把 n 变成完全平方数的方案数。
Sample Input
2
7844
9121
7844
9121
Sample Output
Case 1: 2
Case 2: 0
Case 2: 0
Hint
Problem Idea
解题思路:
【题意】
一个四位数n,问有多少种方案通过恰好修改一个数字,使得新得到的四位数是一个完全平方数
【类型】
暴力
【分析】
对于四位数n,格式如下:
最多有9000种情况,所以我们可以大胆的暴力求解
但在这之前,为了便于完全平方数的判定,我们可以先将四位数中的完全平方数给标记出来
因此,只需预处理出32~99的平方数,并做记录
这样就可以暴力修改某位数字,然后直接判断是不是平方数
因为要恰好修改一位数字,所以不修改的肯定是不合要求的
还有就是最高位为0的也要抹杀掉
【时间复杂度&&优化】
O(n)
题目链接→CSU Problem 1785 又一道简单题
 Source Code
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 10005;
const int M = 4;
const int inf = 1000000007;
const int mod = 1000003;
bool v[N];
char s[M];
int main()
{int t,i,j,n,k,ans,p=1;for(i=32;i<100;i++)v[i*i]=true;scanf("%d",&t);while(t--){ans=0;scanf("%s",s);n=atoi(s);for(k=1000,i=0;i<4;i++,k/=10)for(j=0;j<=9;j++){if(i==0&&j==0||s[i]-'0'==j)continue;if(v[n-(s[i]-'0'-j)*k])ans++;}printf("Case %d: %d\n",p++,ans);}return 0;
}