此文章可以使用目录功能哟↑(点击上方[+])

 SPOJ REPEATS - Repeats

 Problem Idea

解题思路:

【题意】

给定一个字符串，求重复次数最多的连续重复子串

【类型】
后缀数组[重复次数最多的连续重复子串]
【分析】

本题是一道裸的后缀数组题

"重复次数最多的连续重复子串"解法(摘自罗穗骞的国家集训队论文):

先穷举长度L，然后求长度为L的子串最多能连续出现几次。首先连续出现1次是肯定可以的，所以这里只考虑至少2次的情况。假设在原字符串中连续出现2次，记这个子字符串为S，那么S肯定包括了字符r[0], r[L], r[L*2],r[L*3], ……中的某相邻的两个。所以只须看字符r[L*i]和r[L*(i+1)]往前和
往后各能匹配到多远，记这个总长度为K，那么这里连续出现了K/L+1次。最后看最大值是多少。如图所示。

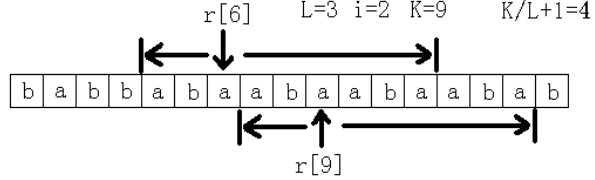
ps：基本思路在罗穗骞的论文里已经说得比较清楚了，而我在这里要提的是论文里比较模糊的部分

要提一提的总共有两点，第一点比较显而易见

“S肯定包括了字符r[0], r[L], r[L*2],r[L*3], ……中的某相邻的两个”

由于当前S是有两个长度为L的连续重复子串拼接而成的，那意味着S[i]和S[i+L](0≤i<L)必定是一样的字符

而这两个字符位置相差L

而字符r[0],r[L],r[L*2],r[L*3],......中相邻两个的位置差均为L

“只须看字符r[L*i]和r[L*(i+1)]往前和往后各能匹配到多远”，对于往后能匹配到多远，这个直接根据最长公共前缀就能很容易得到，即上图中的后缀Suffix(6)和后缀Suffix(9)的最长公共前缀。而对于往前能匹配到多远，我们当然可以一开始就把字符串反过来拼在后面，这样也能根据最长公共前缀来看往前能匹配到多远，但这样效率就比较低了。

其实，当枚举的重复子串长度为i时，我们在枚举r[i*j]和r[i*(j+1)]的过程中，必然可以出现r[i*j]在第一个重复子串里，而r[i*(j+1)]在第二个重复子串里的这种情况，如果此时r[i*j]是第一个重复子串的首字符，这样直接用公共前缀k除以i并向下取整就可以得到最后结果。但如果r[i*j]如果不是首字符，这样算完之后结果就有可能偏小，因为r[i*j]前面可能还有少许字符也能看作是第一个重复子串里的。
于是，我们不妨先算一下，从r[i*j]开始，除匹配了k/i个重复子串，还剩余了几个字符，剩余的自然是k%i个字符。如果说r[i*j]的前面还有i-k%i个字符完成匹配的话，这样就相当于利用多余的字符还可以再匹配出一个重复子串，于是我们只要检查一下从r[i*j-(i-k%i)]和r[i*(j+1)-(i-k%i)]开始是否有i-k%i个字符能够完成匹配即可，也就是说去检查这两个后缀的最长公共前缀是否比i-k%i大即可。
当然如果公共前缀不比i-k%i小，自然就不比i小，因为后面的字符都是已经匹配上的，所以为了方便编写，程序里面就直接去看是否会比i小就可以了。

这部分理解起来有点小困难，还有不懂的欢迎提出

【时间复杂度&&优化】
O(nlogn)

题目链接→SPOJ REPEATS - Repeats

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<list>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 5005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
const int MAXN = 50005;
//rnk从0开始
//sa从1开始,因为最后一个字符(最小的)排在第0位
//height从1开始,因为表示的是sa[i - 1]和sa[i]
//倍增算法 O(nlogn)
int wa[MAXN], wb[MAXN], wv[MAXN], ws_[MAXN];
//Suffix函数的参数m代表字符串中字符的取值范围,是基数排序的一个参数,如果原序列都是字母可以直接取128,如果原序列本身都是整数的话,则m可以取比最大的整数大1的值
//待排序的字符串放在r数组中,从r[0]到r[n-1]，长度为n
//为了方便比较大小,可以在字符串后面添加一个字符,这个字符没有在前面的字符中出现过,而且比前面的字符都要小
//同上,为了函数操作的方便,约定除r[n-1]外所有的r[i]都大于0,r[n-1]=0
//函数结束后,结果放在sa数组中,从sa[0]到sa[n-1]
void Suffix(int *r, int *sa, int n, int m)
{int i, j, k, *x = wa, *y = wb, *t;//对长度为1的字符串排序//一般来说,在字符串的题目中,r的最大值不会很大,所以这里使用了基数排序//如果r的最大值很大,那么把这段代码改成快速排序for(i = 0; i < m; ++i) ws_[i] = 0;for(i = 0; i < n; ++i) ws_[x[i] = r[i]]++;//统计字符的个数for(i = 1; i < m; ++i) ws_[i] += ws_[i - 1];//统计不大于字符i的字符个数for(i = n - 1; i >= 0; --i) sa[--ws_[x[i]]] = i;//计算字符排名//基数排序//x数组保存的值相当于是rank值for(j = 1, k = 1; k < n; j *= 2, m = k){//j是当前字符串的长度,数组y保存的是对第二关键字排序的结果//第二关键字排序for(k = 0, i = n - j; i < n; ++i) y[k++] = i;//第二关键字为0的排在前面for(i = 0; i < n; ++i) if(sa[i] >= j) y[k++] = sa[i] - j;//长度为j的子串sa[i]应该是长度为2 * j的子串sa[i] - j的后缀（第二关键字）,对所有的长度为2 * j的子串根据第二关键字来排序for(i = 0; i < n; ++i) wv[i] = x[y[i]];//提取第一关键字//按第一关键字排序 (原理同对长度为1的字符串排序)for(i = 0; i < m; ++i) ws_[i] = 0;for(i = 0; i < n; ++i) ws_[wv[i]]++;for(i = 1; i < m; ++i) ws_[i] += ws_[i - 1];for(i = n - 1; i >= 0; --i) sa[--ws_[wv[i]]] = y[i];//按第一关键字,计算出了长度为2 * j的子串排名情况//此时数组x是长度为j的子串的排名情况,数组y仍是根据第二关键字排序后的结果//计算长度为2 * j的子串的排名情况,保存到数组xt = x;x = y;y = t;for(x[sa[0]] = 0, i = k = 1; i < n; ++i)x[sa[i]] = (y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + j] == y[sa[i] + j]) ? k - 1 : k++;//若长度为2 * j的子串sa[i]与sa[i - 1]完全相同,则他们有相同的排名}
}
int Rank[MAXN], height[MAXN], sa[MAXN], r[MAXN];
void calheight(int *r,int *sa,int n)
{int i,j,k=0;for(i=1; i<=n; i++)Rank[sa[i]]=i;for(i=0; i<n; height[Rank[i++]]=k)for(k?k--:0,j=sa[Rank[i]-1]; r[i+k]==r[j+k]; k++);
}
int n,minnum[MAXN][16];
void RMQ()   		//预处理  O(nlogn)
{int i,j;int m=(int)(log(n*1.0)/log(2.0));for(i=1;i<=n;i++)minnum[i][0]=height[i];for(j=1;j<=m;j++)for(i=1;i+(1<<j)-1<=n;i++)minnum[i][j]=min(minnum[i][j-1],minnum[i+(1<<(j-1))][j-1]);
}
int Ask_MIN(int a,int b) 	//O(1)
{int k=int(log(b-a+1.0)/log(2.0));return min(minnum[a][k],minnum[b-(1<<k)+1][k]);
}
int calprefix(int a,int b)
{a=Rank[a],b=Rank[b];if(a>b)swap(a,b);return Ask_MIN(a+1,b);
}
char s[5];
int main()
{int t,i,j,k,ans,Max;scanf("%d",&t);while(t--){Max=1;scanf("%d",&n);for(i=0;i<n;i++){scanf("%s",s);r[i]=s[0]-'a'+1;}r[i]=0;Suffix(r,sa,n+1,3);calheight(r,sa,n);RMQ();for(i=1;i<=n;i++){for(j=0;j+i<n;j+=i){ans=calprefix(j,j+i);k=j-(i-ans%i);ans=ans/i+1;if(k>=0&&calprefix(k,k+i)>=i)ans++;//printf("L=%d,R=%d\n",i,ans);Max=max(Max,ans);}}printf("%d\n",Max);}return 0;
}