Game Theory and Multi-agent Reinforcement Learning 笔记1

前言

这是一篇综述性质的文章，里面有个别错字。强化学习最初是针对马尔科夫决策过程（MDP）开发出来的，能使单agent在随机平稳环境（stochastic stationary environment）中学到一个策略最大化一个可能的延迟奖励信号（delayed reward signal）。**在agent能成功实验和操作的环境是马尔科夫的条件下，保证收敛至最优策略。**然而当多智能体在共享的环境中应用强化学习，这或许会超过了MDP模型。在这样的系统中，一个agent的最优策略不仅仅依赖于环境，还有其他agents的策略。这种情形在多种领域很自然地出现，比如机器人、电信、经济、分布式控制、拍卖、交通灯控制。这些领域使用多智能体系统，要么因为领域的复杂性，要么因为控制本身是分散的。在这样的系统，agents能通过与别的learners合作或者竞争发现手上问题的解法是很重要的。本文描述了一个基于博弈论经济学研究的基本学习框架，并说明了这种系统中产生的额外的难题，还描述了一些具有代表性的算法。

介绍

单agent强化学习通过试错法（trial-and-error）与环境交互学习最优行为，但当多个learners在一个共享环境中同时应用强化学习，传统方法通常会失败。
在多agent设置中，经常违反保证收敛所需的假设。即使在agents共享固定环境并需要为了单个状态学习策略的最基本情况下，也会出现许多新的难题。当agents目标一致并且所有agents都试图最大化相同的奖励信号时，仍然需要协调才能达到全局最优。当agents有相反的目标时，一个明确的最优解决方案可能不再存在。在这种情况下，通常寻找agents策略之间的平衡。在这种均衡中，当其他agents保持其行为固定时，任何代理人都不能提高其收益。
当环境变成需要多个序列决策的动态环境时，问题会更复杂，agents不仅要协作，还要考虑当前环境的状态。但agents典型情况下只有系统的有限的信息。整体上，他们或许无法观察到其他agents的动作或奖励，即使这些动作对他们的环境和奖励会有直接的影响。最难的是，agent或许不知道其他agents的存在，使得环境似乎是不平稳的。另一种情况，agents可以获得所有这些信息，但由于计算的复杂性和agents之间所需的协调性，在一个完全联合状态-动作空间学习是不现实的。

多智能体强化学习的发展基于两大支柱：人工智能里的强化学习研究和博弈论上的跨学科工作。博弈论既提供了描述多智能体学习问题设置的方法，又提供了分析学习结果的工具。
本文讨论的MAS中的agents是自治实体，有独立的目标，独立的决策能力，但会被彼此的决策影响。
无状态博弈，致力于解决静态环境下多智能体的交互。
马尔科夫博弈，解决多智能体的交互和动态环境。
独立learners只基于自己的奖励观察学习。
联合动作learners还观察其他agents 的动作和可能的奖励。

Repeated Games

博弈论

博弈论的核心思想是将战略互动建模为一组参与者之间的博弈。
Extensive form games，表示参与者轮流执行动作。
Normal form games，参与者同时选择独立的动作执行。

Normal form games

a是一个联合动作，Rk（a）是agent k的期望收益。
Normal form games使用收益矩阵（payoff matrix）表示。行是玩家1，列是玩家2，每一项是两个玩家在该联合动作下的对应收益。

策略是agent k动作集上概率分布集的一个元素。如果一个动作的概率是1，其余为0，这是纯策略，否则是混合策略。Normal form games的一个重要假设是期望收益在玩家的策略里是线性的。

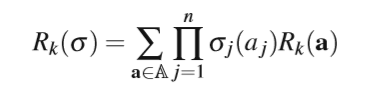
对联合动作集中的每个联合动作，得到该agent对这个联合动作的reward，乘上所有agents执行联合动作中对应动作的、各自策略中动作概率的积，该策略就是策略组合中的策略，再把所有联合动作的期望加起来，得到agent k在这个策略组合下的期望奖励。

博弈的类型

共同利益博弈（identical payoff or common interest game）所有的玩家有同样的奖励函数。
零和博弈（zero-sum game）所有玩家的奖励加起来为0，也称为纯对抗博弈。其余为一般和博弈（general sum game）。

第二个，k越小，越难在解决方案上达成一致。

博弈的解决概念

不能简单的最大化所有参与者的收益，因为或许不可能所有的参与者同时达到这一目标。一个重要的概念就是best response，根据博弈中对手的策略最大化他的收益。概念定义如下：

在纳什均衡中，参与者都使用彼此最好的回应，每个人都使用best response。每个normal form game都至少有一个纳什均衡，可能是混合策略。纳什均衡可以定义如下：

因此，当玩纳什均衡时，博弈中的任何玩家都不能通过单方面偏离均衡策略来提高自己的收益。因此，没有一个玩家有动机改变他的策略，而多个玩家必须同时改变他们的策略，以摆脱纳什均衡。

强化学习在repeated games

不像博弈论的设置，agent假定无法获知收益矩阵。agents是博弈中的玩家，重复地玩来提升自己的策略。
值得注意的是，repeated games没有捕获完整的多智能体强化学习问题。期望奖励的改变仅仅因为其他玩家策略的改变，agents外部没有变化的环境状态和状态转移函数。因此repeated games有时也叫无状态博弈（stateless games）。不过也给独立学习agents提供了挑战性的问题，并且适用于测试协同的方法。
与传统经济学博弈论不同的是，agents无法得知奖励函数，也不知道期望收益。
开发多智能体强化学习应用程序时，必须考虑特定设置中的可用信息，以便将此设置与适当的技术相匹配。

学习目标

通常最大化博弈中所有玩家的收益是不可能的，因此大多数RL方法尝试实现纳什均衡，但有很多缺点：

1. 纳什均衡不一定唯一，造成了均衡选择问题。当这些纳什均衡具有相同的质量时，导致了agents间的协同问题。例子表14.3（b）。
2. 即使在一个均衡中，玩家有不同的期望收益，不同的玩家有不同的偏好的均衡结果，因此需要确保他们协同在一个均衡上。例子表14.2（b）。
3. 纳什均衡不保证最优。比如14.2（c），非纳什均衡的结果是最优的。

纳什均衡虽然用的多，但不是唯一的解决概念。Correlated Equilibrium(CE))、 Evolutionary Stable Strategy (ESS)。
repeated games中日常使用的评价标准是regret——agent实现的最大收益与使用某种固定策略获得收益的差。给定agent k，时间T的玩耍历史，全部regret定义如下：

准确的计算需要奖励函数和其他agents动作的观察，否则则需要根据之前的观察估计。在某些假定下，基于regret的学习可以收敛于某种形式的均衡。

博弈中的Q-learning

每个玩家保存自己的q值向量，不用博弈中其他玩家的任何信息。无状态版本的q-learning更新如下：

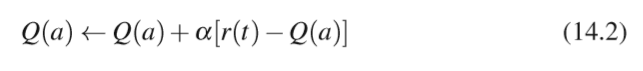
尽管独立Q-learners在某些情况下表现出达到均衡，他们也表现出在某些博弈中无法协调，甚至在其他游戏中无法完全收敛。
联合动作learners学习所有联合动作的Q值，换句话说，每个agent j为A中的所有a学习q值。
每个agent根据对其他agent策略的信任独立进行动作选择。联合动作的Q值是expected values，agent i执行动作的EV定义如下：

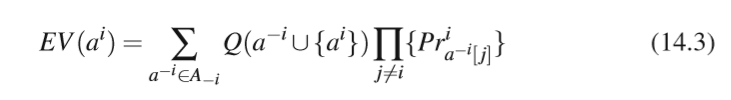
思路类似上面求某个agent策略组合期望收益的公式。这个是针对所有的其他agents的动作组合，求联合动作Q值与各agents执行相应动作的概率的乘积，再将所有包含agent i该动作的动作组合的期望值加起来。
联合动作learners与独立learners行为相似。需要更复杂的探索策略才能提高收敛到最优纳什均衡的概率。简单探索策略不成功的原因主要是由于包含在最优纳什均衡的动作，与其他动作结合时往往导致回报率低得多，因此低估了该动作的潜在质量。
frequency maximum Q-learning (FMQ) 使用某个动作获得最大奖励的频率来进行启发式搜索，可以在确定性收益的共同利益博弈中找到最优解：

承诺序列是agent承诺始终选择相同操作的时段列表，可以发现两种不确定性的源头：奖励信号的噪声、其他agents执行动作对reward的影响，可以处理随机收益博弈里的独立学习，即联合动作并不总是导致同样的确定性收益给每个agent。

梯度上升方法

学习自动机（LA）是相对简单的策略迭代器，它保存动作集A上的动作概率向量p。最常用的LA更新方案是Linear Reward-Penalty ，如下方式更新动作概率：

这些学习计划在游戏环境中表现良好，即使它们不需要游戏中其他玩家的任何信息（行动、奖励、策略）。每个agent独立地应用LA更新规则来更改其操作的概率。
在两人零和博弈中，LR-L收敛到纯策略的纳什均衡，LR-epsilonP能估计混合均衡。在n-player共同利益博弈， reward-inaction 也收敛到一个纯纳什均衡。下列属性是LR-I的动态：

1. 所有纳什平衡都是平稳点。
2. 所有严格的纳什均衡都是渐近稳定的。
3. 所有非纳什平衡点都是不稳定的。

使用reward-inaction 方案的自动机团队将收敛到概率为1的纯联合策略，以及在具有随机回报的冲突利益博弈。这些结果加在一起意味着在N-player的一般和游戏中，局部收敛于纯纳什均衡。由于具有较高回报的纳什均衡对LA具有更强的吸引力，agents更可能达到更好的纳什均衡。配备了一个只需要非常有限的通信的探索策略，agents可以在不需要进行详尽探索的情况下探索有趣的纳什均衡，一旦找到这些，就可以考虑不同的解决方案概念，例如在不同的帕累托最优解之间交替出现的恰当解。（这一句我不太懂）这些基于LA的方法能够在agents异步执行操作和延迟奖励的环境中收敛，这在负载平衡设置或拥塞游戏中很常见。
博弈中经常研究的另一种梯度技术是极小梯度上升（IGA）算法家族。