学习depthwise卷积时看的一篇文章,简要记录
Wang, Min, Baoyuan Liu, and Hassan Foroosh. “Design of Efficient Convolutional Layers using Single Intra-channel Convolution, Topological Subdivisioning and Spatial “Bottleneck” Structure.”
arXiv:1608.04337v2
本文提出了一种新的卷积方式,输入和输出通道的数量与经典模型相同,但可以根据精确度优化卷积以及连接的数量,独特之处有三:
- 通过展开卷积来降低复杂度
- 在保持局部正则性的前提下,利用拓扑结构使卷积层的连接变得稀疏
- 使用一个conv-deconv瓶颈来减少卷积,同时保持分辨率
概要
- 每个卷积层上的三维卷积运算可以看作是在每个通道上进行空间卷积,同时进行跨通道的线性投影。
文章思路:
- 在标准的卷积层中,三维卷积可以看作是导致了计算冗余的单通道内的空间卷积和线性通道投影,这两个操作首先在每个通道和随后的线性通道投影中展开为一组2D卷积。
- 然后进一步的修改,按顺序而不是并行执行二维卷积。通过这种方法,获得了一个单一的通道内卷积(SIC)层,该层对每个输入通道和线性通道投影只涉及一个滤波器,从而大大降低了复杂度
- 通过叠加多个SIC层,可以训练比基于标准卷积层的模型效率高几倍的模型
- 采用拓扑子划分减少输入通道与输出通道的连接。
线性信道投影消耗了大部分的计算量。为了减少其复杂性,在输入通道和输出通道之间提出一个拓扑子划分框架,如下:——把输入和输出通道首先被重新排列成一个s-dimensional张量,然后每个输出通道只连接到在其附近的输入通道。该框架形成了规则的卷积核稀疏模式,实验表明,该模式比标准卷积层具有更好的性能/代价比。
- 还引入了一种空间“瓶颈”结构,它利用卷积-投影-反卷积的流水线来充分利用输入中相邻像素之间的相关性
首先通过信道内步长卷积降低空间维数,然后通过线性信道投影后的相同步长反卷积恢复空间维数。这种设计在不牺牲空间分辨率的情况下降低了线性通道投影的复杂性。
方法
假设输出通道的数量与输入通道的数量相等,并且对输入进行padding,以便输出的空间维度与输入相同。假设对每个卷积层都应用了残差学习技术,即由于它们的维数相同,输入直接加到输出。
Standard Convolutional Layer Consider
先来复习一下卷积的运算过程。伪代码如下:

标准卷积将3D卷积核(红色)放置在输入数据 I(左侧)上,对位相乘得到输出O(右侧)的一个像素(橙色)。

卷积核在一个通道上的尺寸为,输入、输出通道数分别为n,n。
当下流行的网络中,卷积层的主要作用是提取特征,往往会保持图像尺寸不变。缩小图像的步骤一般由pooling层实现。这里认为输入输出的尺寸相同,都是h×w。
计算一个输出像素所需乘法次数为:
总体乘法次数为:
n,n体现了对于特征的挖掘,取值较大,常为几百;相反,由于复杂度与内核大小成二次关系,在最近的CNN模型中,内核大小被限制为3×3来控制总体运行时间,(k一般在1~5左右,很少超过7),高层次特征通过多个小尺寸卷积层实现。
Single Intra-Channel Convolutional Layer
三维卷积运算可以看作是各通道内的二维空间卷积和通道间的线性投影的结合。
在第一个步骤中,输入的每一通道单独运算。在同样尺寸卷积核的作用下,每一通道计算得到b层结果。m通道数据变为m×b通道。中间结果的每一通道称为一个基层basis。
在第二个步骤中,各个通道进行合并,但使用的卷积核尺寸为1。
空间卷积能够捕获局部结构信息,而线性投影则通过变换特征空间来学习神经元层中必要的非线性。具体的:
- 每个输入通道首先与b个2Dfilter进行卷积,生成具有输入通道b倍的中间特征。
- 然后通过线性通道投影产生输出。
- 通过调优b和k,可以得到更多的模型
如算法2所示,总体乘法次数为:
- k比n小得多
- 复杂度与b近似成线性关系
- 当b = k^2时,这是等价于标准卷积层的线性分解
- 当b < k^2时,复杂度以低秩的方式低于标准卷积层。
文章提出,与同时对每个输入通道进行二维滤波器卷积不同,可以按顺序进行卷积。意思是,上面对每个通道使用b个filter的卷积层可以转换为具有b层的框架。对于相同的b,n取值,此网络乘法数量和原来相同。但由于原来的并行计算改为串行(相当于增加深度),同时引入残差结构,此种网络的性能更佳 .


残差连接作用:当我们考虑b层中的每一层时,只有一个k×k核与输入通道卷积。但是仅用一个过滤器进行卷积不能保存输入数据中的所有信息,而且很难自由地学习所有有用的局部结构。实际上,这可能会导致低通滤波器,它在某种程度上相当于图像的第一个主成分,因此引入残差连接。
提速示例
n k b rate 128 3 1 11.9% 128 3 5 59.5% 128 3 8 95.1% 128 5 8 38.3%
如果原有卷积核k=1,这种方法无法提速。
Topologica Subdivisioning
提出在卷积层的输入和输出通道之间的s维拓扑子划分。换句话说就是减少输出通道和输入通道的连接数量。即,输出通道不再和所有输入通道有关,只和相邻的输入通道有关。最直观的想法是,定义一个邻域大小c,每一个输出通道只和相邻的c个输入通道有关。
假设输入通道和输出通道的数量都为n,首先将输入和输出通道排列为一个s维张量[d1, d2,…ds],有:
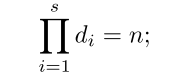
?
每个输出通道只连接到它在张量空间中的局部邻域,而不是所有的输入通道。局部邻域由另一个s维张量定义,[c1, c2,…, cs],每个输出通道的邻域总数为:

?
计算复杂度与原始卷积相比,节省c/n。
 ?
? ?
?
当k = 1时,该算法适用于线性投影层,可以直接嵌入算法2,进一步降低SIC层的复杂度。
Spatial “Bottleneck” Structure
一个卷积层的复杂度是由空间维度和通道数量乘积决定的。为了保持可接受的复杂度,在增加通道数量的同时,通过最大池化或跨步卷积来降低空间维数。
另一方面,在每个卷积层的输入中,相邻的像素是相互关联的,特别是在空间分辨率高的情况下。通过简单的下采样来降低分辨率显然会导致信息的丢失,但这种相关性具有相当大的冗余,可以加以利用。论文引入一个空间“瓶颈”结构,利用输入的空间冗余,在不降低空间分辨率或通道数量的情况下减少计算量。
考虑3D输入数据 I 在中,首先对每个输入通道应用一个单独的通道内卷积。将一个步长为k的k×k核与每个输入通道卷积,使输出维度降为
。然后应用一个线性投影层。最后用步长 k进行k×k通道内反卷积,恢复空间分辨率

?
消耗大部分计算的线性投影阶段比原始输入的普通线性投影效率高k^2倍。通道内卷积和反卷积阶段学习捕获邻近像素的局部相关性,同时保持输出的空间分辨率。
实验
baseline model
选择ImageNet分类问题为实验对象。首先使用标准卷积层设计标准网络A作为参照。基本结构如下: ?
?
对于不太深的网络,Residual结构对精度提升不大,主要作用是加速训练过程。
Single Intra-Channel Convolutional Layer
- 首先用模型B中展开的卷积配置替换标准卷积层。每个输入通道由4个滤波器卷积,因此B的复杂度约为基线模型的4/9。
- 使用两个SIC层替换一个标准的卷积层。模型C比基准模型A有更多的层,但它的复杂性只有A的2/9.
- 将SIC层的数量从模型C的4层增加到模型E的6层,模型E的复杂度只有基线中的1/3。由于SIC层极低的复杂性,可以很容易地增加模型深度而不需要太多的计算量.
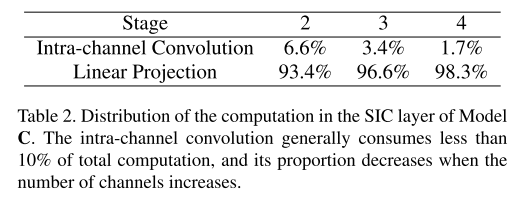
- 表2列出了模型C中每个SIC层的通道内卷积和线性信道投影之间的计算分布。通道内卷积通常消耗的计算量不到总层开销的10%。由于这个优势,可以利用更大的内核大小,而只牺牲很小的效率。将模型C的核大小设置为5,得到模型D:
结论:表3列出了从A到E的top-1和top-5的误差以及模型的复杂程度。
- 比较模型B和模型A,在相同的层数下,模型B可以用不到一半的计算量与模型A相匹配。
- 在比较基于SIC的模型C和模型B时,模型C将top-1的误差降低了1%,复杂度减半。这验证了所提出的SIC层的优越效率。
- 当使用5*5核时,模型E平均在复杂度增加5%的情况下获得0.5%的精度增益。这说明在SIC层中增加内核的大小为提高精确度和复杂度比提供了另一种选择。

Topological Subdivisioning
模型F采用二维拓扑,两个维度都有ci = di/2,使得复杂性降低了4倍。在模型G中,使用了3D拓扑,并设置了ci和di,使得复杂性降低了4.27倍。拓扑层的数目是标准层数目的两倍,所以每个阶段的总复杂度减少了1 / 2。

作为比较,还引入AlexNet的直接分组策略训练模型H。输入和输出通道均分为4组。每组的输出通道只依赖于对应组的输入通道。通过这种方式,复杂性也降低了4倍。表5列出了结果。

- 在复杂度相同的情况下,二维和三维拓扑模型都优于分组方法,错误率更低。
- 与基线模型相比,两种拓扑模型的top-1和top-5错误率相似,计算量减半。
- 最后,将拓扑子划分应用到模型I中的SIC层。根据表5的结果选择二维拓扑。在模型I中,由于SIC层和拓扑子划分造成的层翻倍,每一阶段有8个卷积层。然而,每一层的复杂度大约只有标准的3* 3卷积层的1/36。与基线模型1相比,2D拓扑加上SIC层的错误率相似,但速度快了9倍。
Spatial “Bottleneck” Structure
通道内卷积和反卷积的核大小和步长均设置为2
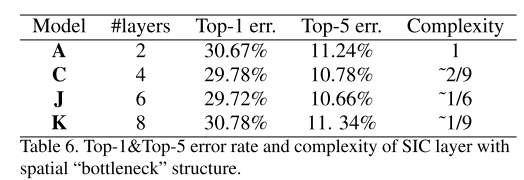
模型J和模型K都对模型C进行了修改,将SIC层替换为空间“瓶颈”层。一个SIC层被两个空间“瓶颈”层所取代,第一个层没有填充,第二个层只有一个像素填充,从而降低了50%的复杂度。在模型J中,每隔一层SIC被替换;在模型K中,替换了所有的SIC层。表6比较了它们与基线模型和基于SIC的模型的性能。与SIC模型C相比,模型J在不损失精度的情况下降低了25%的复杂性;模型K将复杂性降低了50%
Comparison with standard CNN models
逐步增加每个阶段具有通道式瓶颈结构的SIC层数,从8层增加到40层,并将其复杂度与CNN最近的模型进行比较。模型L, M, N, O分别对应8层,12层,24层,40层。相对于VGG、Resnet-34、Resnet-50和Resnet-101,模型效率分别提高了42倍、7.3倍、4.5倍和6.5倍,top-1和top-5的误差也基本相同。


Visualization of filters
采用文章提出方法学习的核具有更高层次的正则化结构,而标准卷积层的核具有更多的随机性。认为这是由于减少了滤波器的数目而使正则化更强。