CNN经典网络：LeNet、AlexNet、NIN、VGG

LeNet

CNN的开山之作，是LeCun在98年解决手写是数字识别任务时提出的，从那时起CNN的基本架构就定下来了：卷积、池化、全连接层。

网络结构

• 如图 3.1 所示，最早的 LeNet 有 7 层网络，包括 3 个卷积层， 2 个池化层，2 个全连接层，其中输入图像的尺寸是 32x32。
• C1 层为卷积层，有 6 个 5*5 的卷积核，原始图像送入卷积层，因此生成了6 个（32-5+1） x（32-5+1） =28x28 的 feature map， 这一层需要训练的参数为（5x5+1） x 6 =26 x 5 = 156 个参数，其中 5x5 是卷积核尺寸， 1 是偏置参数， 所以对应 6个 28x28 feature map,连接数为 6x26x28x28=122304；
• S2 层为池化层，所用到的是 2x2 最大池化来进行降维，得到 6 个 14x14 的feature map， 池化的过程是通过将每四个输入相加乘以一个系数再加上一个偏置参数，因此 S2 层所需要训练的参数为 2x6=12 个，连接数为（4+1)x6x14x14=5880；之后通过 Sigmoid 函数激活，送入下一层；
• C3 层是卷积层，有 16 个卷积核，每一个卷积模板是 5x5，每一个模板有 6个通道，但是这一层并不是全连接，而是与输入层部分连接，以 feature map0为例，用到的是 3 通道的 5x5 卷积核分别与上一层的 feature map 0,1,2 连接，得到的新的 feature map 大小为（14-5+1） x（14-5+1） =10x10，因此输出为 16个 10x10 的 feature map， 所需要训练的参数为（25x3+1） x6+（25x4+1） x9+
  （25x6+1） =1516 个参数；连接数为 1516x10x10=151600；

• S4 层为池化层，与 S2 层相同， 2x2 最大池化，得到了 16 个 5x5 的 feature map， 送入 Sigmoid 激活函数送入下一层；需要的参数是 2x16=32，连接数为（4+1） x16x5x5=2000；
• C5 层为卷积层，有 120 个卷积核，每一个卷积模板是 5x5，每一个模板有16 个通道，得到 120 个 1x1 feature map（相当于全连接）； 训练参数为 120x（5x5x16+1）=48120，连接数为 48120；
• F6 层为全连接层，有 84 个神经元，与上一层 120 个 1x1feature map 全连接，得到 84 维特征向量；连接数为 120x84=10080；最后利用 84 维特征向量进行分类预测；
• O7 层为输出层， 每一个类有一个RBF（Euclidean Radial Basis）功能单元，即径向欧式距离函数。每个单元有 84 个输入，输出 yi 按照如下公式计算

  

  
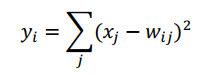
  也就是计算输入向量与参数向量之间的欧式距离。

---

AlexNet

2012 年 ImageNet Challenge 大赛上横空出世的 AlexNet 刷新了 Image Classificationde 记录，也正式引领了深度学习的热潮。

论文：http://202.119.24.249/cache/9/03/papers.nips.cc/40659828b5f8741d01b4efeb826c7f06/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf

特点

• 提出用 ReLU 代替 Sigmoid 激活函数，因为 ReLU 是一种不饱和的非线性函数，具有更快的收敛速度，可以加速拟合训练集；相对于 Sigmoid 函数，只需要一个阈值就可以得到激活值，而不用复杂的运算；
• 提出 GPU 训练，甚至多个 GPU 并行运算，加速了训练速度而且解决了单个 GPU 内存不足的问题；
• 提出数据增强的概念，对于原始图片经过随机裁剪、平移旋转等操作，增加训练样本；
• 提出 Dropout 的概念，对每个隐层神经元的输出有 0.5 的概率置 0，置 0的神经元不会参加前向传播核反向更新，从而防止过拟合，代价是训练迭代的次数增加一倍。

网络结构

如图 3.3 所示， AlexNet 采用的是两台 GPU 服务器，分为上下两组，该模型一共分为八层，五个卷积层以及三个全连接层，在每一个卷积层中包含了激励函数 ReLU 以及局部响应归一（LRN）处理，然后在经过降采样（pool 处理）。

1. 第一层 conv1 卷积层，输入的原始图像是 227x227x3 的 3 通道 RGB 图像，原始图像被 96 个 11x11x3 的卷积核进行卷积运算，卷积过程的步长为 4，所以生成了[（227-11） /4+1]x[(227-11)/4+1]=55x55 尺寸的 feature map， 共有 96个，分为 2 组每组 48 个 55x55 特征映射，经过 relu 单元激活生成仍是 2 组55x55x48 特征映射；再经由 Max pooling 池化运算尺度为 3x3，步长为 2，因此池化后的尺寸为[（55-3） /2+1]x[（55-3） /2+1]=27x27，分在 2 个 GPU 上，每组为 27x27x48 feature map；
2. 第二层 conv2 卷积层，输入数据为前一层的27x27x96，为了后续处理，每幅特征映射左右上下各填充 2 个像素，每组被 48 通道的 5x5 卷积模板进行卷积运算，第二层共有 256 个卷积核，卷积后得到[（27-5+2x2） /1+1]x[（27-5+2x2） /1+1]=27x27； 共有 256 个 27x27 的 feature map， 分在 2 个 GPU，每组各 128 个； 经由 relu 单元激活后送入 Max pooling， 依旧是步长为 2 的 3*3 池化尺度，得到[（27-3） /2+1]x[（27-3） /2+1]=13x13 的特征映射，分在 2 个 GPU，每组 128 个 13x13 的 feature map；
3. 第三层 conv3 卷积层，输入数据为前一层的 13x13x256，为了后续处理，每幅特征映射左右上下两边都要填充 1 个像素；每组被 256 通道的 3x3 卷积模板，第三层共有 384 个卷积核，卷积后得到[（13-3+1x2） /1+1]x[（13-3+1x2）
   /1+1]=13x13；共有 384 个 13x13 的 feature map， 分在 2 个 GPU，每组各 192个；经由 relu 单元送入第四层；
4. 第四层 conv4 卷积层，输入数据为前一层的 13x13x384，为了后续处理，每幅特征映射左右上下两边都要填充 1 个像素，每组被 192 通道的 3x3 卷积模板，第四层共有 2 组 192 共 384 个卷积核，卷积运算后得到[（13-3+1x2）/1+1]x[（13-3+1x2） /1+1]=13x13；共有 384 个 13x13feature map， 分在 2 个GPU，每组各 192 个；经由 relu 单元送入第五层；
5. 第五层 conv5 卷积层，输入数据为前一层的 13x13x384，为了后续处理，每幅特征映射左右上下各填充 1 个像素， 每组被 192 通道 3x3 卷积模板，第五层共有 256 个卷积核，卷积后得到[（13-3+1x2） /1+1] x[（13-3+1x2）/1+1]=13x13； 共有 256 个 13x13 的 feature map，分在 2 个 GPU，每组各 128个；经由 relu 单元送入池化，池化尺度为 3x3，步长为 2，池化得到尺寸（13-3） /2+1=6，得到了 2 组 6x6x128 个 feature map；
6. 第六层 fc6 全连接层，输入数据为 6x6x256，采用 6x6x256 尺寸滤波器进行卷积运算，每次卷积运算生成一个运算结果，通过一个神经元输出,共有 4096个 6x6x256 尺寸的滤波器对输入数据进行运算，通过 4096 个神经元输出，经过relu 单元生成 4096 个值，并通过 drop 运算输出 4096 个结果；
7. 第七层 fc7 全连接层，第 6 层输出 4096 个数据与第七层 4096 个神经元进行全连接，经由 relu 单元生成 4096 个数据，再经由 dropout7 处理后输出 4096 个数据；
8. 第八层 fc8 全连接层，第 7 层输出的 4096 个数据与第八层 1000 个神经元进行全连接，经过训练后输出被训练的数值。

---

NIN

NIN改进了传统的CNN，采用了少量参数就取得了超过AlexNet的性能，AlexNet网络参数大小是230M，NIN只需要29M

论文：https://arxiv.org/pdf/1312.4400.pdf

网络结构

如图 所示，网络总共四层，3mlpconv + 1global_average_pooling，主要创新在于 MLP 以及全局均匀池化部分，通过增强卷积模块的方式加强了模型的分类能力。

传统的卷积网络用卷积提取特征，然后得到的特征再用FC+softmax逻辑回归分类层进行分类。
使用全局平均池化层，每个特征图作为一个输出。这样参数量大大减小，并且每一个特征图相当于一个输出特征（表示输出类的特征）。

特点

• 提出了 MLP（多层感知机，多层全连接层和非线性函数的组合） 对卷积层进行改进，传统的卷积层只是将前一层特征进行线性组合，然后进行非线性激活[蓝框部分]，而在传统卷积层之后增加一个微小的神经网络 [绿框部分]对之前的特征进一步抽象，实现了对于同一个像素点的跨通道的组合，也就是可以等效为 1x1 的卷积核， 1x1 卷积核还可以用来降维，从而减少训练的参数；

以前的卷积层，局部感受野运算仅仅是是一个单层的神经网络（线性滤波器对图像进行内积运算，跟着一个非线性激活函数），mlpconv层可以看成局部感受野上进行conv运算之前，还进行mlp运算，而MLP网络中，常见的使用三层的全连接结构，等效于普通卷积后，再添加一个1:1的卷积和Relu函数

优点：

• 提供了网络层间映射的一种新可能；
• 增加了网络卷积层的非线性能力。

• 提出了全局平均池化代替全连接层，除了能够强化特征图与类别的关系，最重要的是不需要训练参数，可以避免过拟合，主要通过对于每一个特征图求出平均数，然后再将平均数组成特征向量输入 softmax 层中进行分类。

Global Average Pooling主要为了解决全连接层参数过多的问题，早期对于分类问题，最后一个卷积层的 Feature Map 通常与全连接层连接，最后通过 softmax 逻辑回归分类。全连接层带来的问题就是参数空间过大，容易过拟合。早期 Alex 采用了Dropout 的方法，来减轻过拟合，提高网络的泛化能力，但依旧无法解决参数过多问题。
全连接层的存在有以下缺点：

• 全连接层是传统的神经网络形式，使用了全连接层是因为卷积层只是作为特征提取器来提取图像的特征，而全连接层是不可解释的，从而CNN也不可解释了。全连接层中的参数往往占据CNN整个网络参数的一大部分，从而使用全连接层容易导致过拟合。

Global Average Pooling的做法是将全连接层去掉，在最后一层，将卷积层设为与类别数目一致，然后全局pooling，从而直接输出各个类别结果。

使用全局平均 pooling 代替全连接层，使得最后一个多层感知卷积层获得的每一个特征图能够对应于一个输出类别，优点如下：

• 全局平均池化更原生的支持于卷积结构，通过加强特征映射与相应分（种）类的对应关系，特征映射可以很容易解释为分类映射
• 全局平均池化一层没有需要优化的参数，减少大量的训练参数有效避免过拟合
• 全局平均池化汇总（求和）空间信息，因此其对空间变换是健壮的

---

VGG

VGGNet 在 AlexNet 的基础上提出了加深网络深度的方法来提高模型分类的能力，并一举获得了 ILSVRC 2014 的亚军。（冠军为GoogLeNet）
论文：https://arxiv.org/pdf/1409.1556.pdf

特点

• 加深了网络的深度，由 AlexNet8 层加深到了 19 层，提高了模型的分类能力；
• 利用多个小卷积核来代替大卷积核；例如用 3 个 3x3 的卷积层，层与层之间有非线性激活函数，可以获得 7x7 卷积层的感受野，但是对于 7x7 卷积核需要 7x7xcxc=49c^2 个参数，而对于 3 个 3x3 的卷积层组合，则只需要 3x（ 3x3） x c x c=27c^2 个参数；

那么问题来了，2个3x3的卷积核可以替代一个5x5的卷积核吗？
当然可以，我们举一个最简单的栗子：
假设我们卷积核的步长为1，padding为0，输入的图形高度为n，那么我们用5x5的卷积核做一轮卷积运算，得到的图形高度为（（n?5+1）/1=n?4。现在我们用3x3的卷积核对这个相同的输入进行卷积运算：1，第一次卷积得到的高度为（（n?3+1）/1=n?2），现在我们对这个结果再进行一次卷积运算，卷积核依然为3x3，此时得到的卷积高度为：（n?2?3+1）/1=n?4） 显然，两次卷积结果是一样的。

• 采用 Pre-trained 方法利用浅层网络的训练参数初始化深层网络参数，加速收敛；
• 采用 Multi-Scale 方法进行数据增强，通过将图像缩放到不同尺寸随机剪裁，获得多个版本的数据，增加了很多数据量，防止过拟合；

网络结构

1. A： 8 个卷积层， 3 个全连接层，共计 11 层；
2. B：在 A 的 stage2 和 stage3 分别增加一个 3x3 的卷积层， 10 个卷积层，总计 13 层；
3. C：在 B 的基础上， stage3， stage4， stage5 分别增加 1x1 的卷积层， 13 个卷积层，总计 16 层；
4. D：在 C 的基础上， stage3， stage4， stage5 分别增加 3x3 的卷积层， 13 个卷积层，总计 16 层；
5. E：在 D 的基础上， stage3， stage4， stage5 分别增加 3x3 的卷积层， 16 个卷积层，总计 19 层。\

• 第一层卷积

1，首先我们输入一副图片，这个图片的像素尺寸是224x224，由于是彩色图片，有3个通道，因此实际输入尺寸为224x224x3

2，我们引入卷积核，卷积核的大小为3x3，根据我们对卷积核的了解，由于输入是一个3通道的张量，因此卷积核的深度也是3.所以卷积核的实际尺寸为3x3x3

3，根据图例，我们的第一层卷积为224x224x64，这个大小是如何得到的？

根据问题2，我们知道我们引入的卷积核尺寸为3x3，根据上面的表，我们知道步长为1，此时卷积后得到的张量维度应该为（224-3+1）/1=222，因此不难推测，我们对原始输入模型增加了padding：（224-3+1+2）/1=224. 我们知道，通过3x3x3的卷积核对原始输入进行卷积后得到的张量深度为1，因此，我们采用了64个这样的卷积核，最后得到了深度为64的张量。

4，我们引入2x2的最大池化层，缩小数组的维度，由224x224x64变为112x112x64（注意，池化层紧紧是缩小模型的长和宽，不会改变模型的深度，因此这里深度依然为64，而非128）

• 第二层卷积

1，现在我们的输入从原始图像变成了由第一层卷积之后的输出数组：112x112x64. 我们再次引入和之前相同尺寸的卷积核，但是深度由原来的3变成了64（3x3x64），并且引入了128个这个卷积核，因此经过这一轮卷积运算，数组变成了112x112x128.

2，我们引入2x2的池化层，将数组降维变成56x56x128的数组

• 第三层卷积

1，根据上面的思想，我们现在的输入是56x56x128的数组，我们引入尺寸为3x3x128的卷积核，并且引用了256个，此时数组的大小变为56x56x256

2，我们依然引入2x2的池化层，模型降维成28x28x256

• 第四层卷积

1，我们按照上面的思路，首先把模型变为28x28x512的数组

2，通过池化层，将模型降维变成14x14x512的数组

• 第五层卷积

1，我们引入3x3x512的卷积核，但是不改变输入模型的深度，这句话的意思是这种卷积核我们引入512个。

2，通过2x2的池化操作，我们将模型降维变成7x7x512

• 全连接层

这里要注意一下，我们引入了全连接层，那么对于全连接层而言，输入不再是一个7x7x512的矩阵，现在输入可以想象为一个25088的向量（这个25088就是7x7x512的结果），整个全连接层如下图所示：

以上就是VGG16网络的结构。

---

参考博客

https://blog.csdn.net/qq_39751437/article/details/97622636

https://blog.csdn.net/qq_39382877/article/details/97512087