Abstract:
因为深度神经网络难以训练,这篇文章提出了深度残差网络,这个网络不仅比以前的网络深很多,而且可以提升性能。并在各个数据集上表现优异。
Introduction
神经网络的深度对于训练结果是至关重要的,但是当网络开始收敛后,会出现degradation问题,即随着层数的增加,训练误差不降反增。这篇文章引入了残差网络的结构来解决degradation问题。
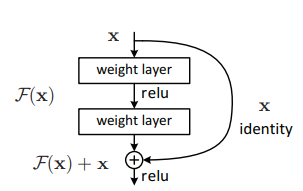
残差网络的一个结构块
Deep Residual Learning
假设一个浅层模型已经训练到饱和(再增加层数精度就会降低),构造一个深度模型,这个模型复制了浅层模型的网络,并将增加的层数作为一个恒等映射,假设这个深度模型的函数为H(X),因为是恒等映射,所以要使H(X)尽量趋近与x(这样就不会导致误差增加),那么这个优化问题就转变成了优化残差函数F(x)=H(X)-x。文章假设优化残差函数比优化原函数更加简单。实现证明,残差结构的确是有效的。
一个通俗的理解:
F是求和前网络映射,H是从输入到求和后的网络映射。比如把5映射到5.1,那么引入残差前是F’(5)=5.1,引入残差后是H(5)=5.1,
H(5)=F(5)+5,
F(5)=0.1。这里的F’和F都表示网络参数映射,引入残差后的映射对输出的变化更敏感。比如s输出从5.1变到5.2,映射F’的输出增加了1/51=2%,而对于残差结构输出从5.1到5.2,映射F是从0.1到0.2,增加了100%。明显后者输出变化对权重的调整作用更大,所以效果更好。残差的思想都是去掉相同的主体部分,从而突出微小的变化,看到残差网络我第一反应就是差分放大器…
转自CSDN原文链接:https://blog.csdn.net/u014665013/article/details/81985082
Network architecture:
Plain network:卷积层主要为3*3的滤波器,设计遵循:(i) 输出特征尺寸相同的层含有相同数量的滤波器;(ii) 如果特征尺寸减半,则滤波器的数量增加一倍来保证每层的时间复杂度相同。我们直接通过stride 为2的卷积层来进行下采样。
Residual network在以上plain网络的基础上,插入shortcut连接,将网络变成了对应的残差版本。如果输入和输出的维度相同时,可以直接使用恒等shortcuts(下图网络中的实线部分)。当维度增加时(下图网络中的的虚线部分),考虑两个选项:(A) shortcut仍然使用恒等映射,在增加的维度上使用0来填充,这样做不会增加额外的参数;(B) 通过通过1*1的卷积改变x的维度,来使维度保持一致。

