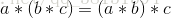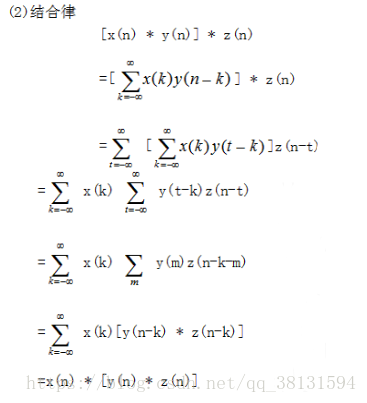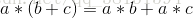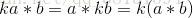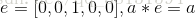Cross Correlation交叉相关:
形象化的描述为,相关为kernel和当前覆盖区域对应元素相乘取和。
" Cross Correlation compares the similarity of two sets of data. Correlation computes a measure of similarity of two input signals as they are shifted by one another. ——correlation is a measure of relatedness of two signals. "[1]
如上所述,交叉相关主要是为了求两组数据的相似度,一个非常重要的应用是NCC(Normalization cross correlation)归一化交叉相关:
其做法类似我们在二维空间中通过求两个向量的cos余弦值来表示两个向量的相似度。当NCC值最大时,两块区域相似的可能性更大。
Convolution卷积:
形象化的描述为,卷积为kernel水平翻转再垂直反转后和当前覆盖区域对应元素相乘取和。
" A convolution is an integral that express the amount of overlap of one function as it is shifted over anot-her function. ——convolution is a filtering operation. "[1]
卷积的主要用处是一个滤波器,之前有在知乎上看到一种从投影角度理解卷积的想法,感觉很新颖也很有说服力:
“ 另一种理解是投影,因为当前模板内部图像和模板的相乘累加操作就是图像局部patch和模板的内积操作,如果把patch和模板拉直,拉直的向量看成是向量空间中的向量,那么这个过程就是patch向模板方向上的投影,一幅图像和一个模板卷积,得到的结果就是图像各个patch在这个方向上的response map或者feature map;如果这样的模板有一组,我们可以把这一组看成一组基,得到的一组feature map就是原图像在这组基上的投影。常见的如用一组Garbor滤波器提取图像的特征,以及卷积神经网络中的第一层,图像在各个卷积核上的投影。 ”[2]
卷积的性质:
- 作为一种线性滤波器(linear filter)卷积满足线性特性:
- 平移不变性(Shift-invariance ):
- 交换律(Commutative):
- 结合律(Associative):
【!!!注意】交叉相关不具有这样的性质,下图为一维卷积结合律的证明,后期会进行修改完善。【来源】
- 加法分配律(Distributes over addition):
- Scalars factor out:
- Identity:
unit impulse
参考资料:
【1】斯坦福 CS131 Computer Vision: Foundations and Applications
【2】知乎:如何理解卷积,另外如何理解图像处理中的卷积?