2022秋季《人工智能》_ch08

题目

基于信息增益，对下述数据集进行决策树构建，描述过程

一个关于配眼镜的一个决策分类所需要的数据，数据集包含4属性：age, astigmatism, trear-prod-rate为输入特征，contact-lenses为决策属性。

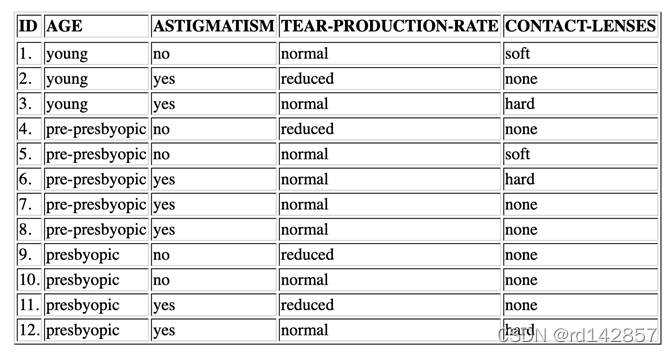
属性集 A = { A G E , A S T , T E A } A=\{AGE,AST,TEA\} A={ AGE,AST,TEA}，类别为$CON$。计算根节点的信息熵
$$Ent(D)=?(\frac{2}{12}{\log }_2\frac{2}{12}+\frac{3}{12}{\log }_2\frac{3}{12}+\frac{7}{12}{\log }_2\frac{7}{12})=1.384$$
计算每个属性的信息熵和信息增益，记$p(soft)=p_1,p(hard)=p_2,p(none)=p_3$，

1. $AGE$

   有三个可能取值 { y o u n g , p r e ? p r e , p r e } \{young,pre-pre,pre\} { young,pre?pre,pre}，对应下标$1,2,3$
   D 1 = { 1 , 2 , 3 } p 1 = 1 3 , p 2 = 1 3 , p 3 = 1 3 E n t ( D 1 ) = ? ( 1 3 log ? 2 1 3 + 1 3 log ? 2 1 3 + 1 3 log ? 2 1 3 ) = 1.585 D 2 = { 4 , 5 , 6 , 7 , 8 } p 1 = 1 5 , p 2 = 1 5 , p 3 = 3 5 E n t ( D 2 ) = ? ( 1 5 log ? 2 1 5 + 1 5 log ? 2 1 5 + 3 5 log ? 2 3 5 ) = 1.371 D 3 = { 9 , 10 , 11 , 12 } p 1 = 0 , p 2 = 1 4 , p 3 = 3 4 E n t ( D 3 ) = ? ( 1 4 log ? 2 1 4 + 3 4 log ? 2 3 4 ) = 0.811 G a i n ( D , A G E ) = E n t ( D ) ? ∑ v = 1 3 ∣ D v ∣ ∣ D ∣ E n t ( D v ) = 1.384 ? 3 12 × 1.585 ? 5 12 × 1.371 ? 4 12 × 0.811 = 0.146 \begin{aligned} &D^1=\{1,2,3\} \quad p_1=\frac{1}{3},\ p_2=\frac{1}{3},\ p_3=\frac{1}{3} \quad Ent(D^1)=-(\frac{1}{3}\log_2{\frac{1}{3}}+\frac{1}{3}\log_2{\frac{1}{3}}+\frac{1}{3}\log_2{\frac{1}{3}})=1.585 \\ &D^2=\{4,5,6,7,8\} \quad p_1=\frac{1}{5},\ p_2=\frac{1}{5},\ p_3=\frac{3}{5} \quad Ent(D^2)=-(\frac{1}{5}\log_2{\frac{1}{5}}+\frac{1}{5}\log_2{\frac{1}{5}}+\frac{3}{5}\log_2{\frac{3}{5}})=1.371 \\ &D^3=\{9,10,11,12\} \quad p_1=0,\ p_2=\frac{1}{4},\ p_3=\frac{3}{4} \quad Ent(D^3)=-(\frac{1}{4}\log_2{\frac{1}{4}}+\frac{3}{4}\log_2{\frac{3}{4}})=0.811 \\ &Gain(D,AGE)=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v)=1.384-\frac{3}{12}\times 1.585-\frac{5}{12}\times 1.371-\frac{4}{12}\times 0.811=0.146 \end{aligned} ?D1={ 1,2,3}p1?=31?, p2?=31?, p3?=31?Ent(D1)=?(31?log2?31?+31?log2?31?+31?log2?31?)=1.585D2={ 4,5,6,7,8}p1?=51?, p2?=51?, p3?=53?Ent(D2)=?(51?log2?51?+51?log2?51?+53?log2?53?)=1.371D3={ 9,10,11,12}p1?=0, p2?=41?, p3?=43?Ent(D3)=?(41?log2?41?+43?log2?43?)=0.811Gain(D,AGE)=Ent(D)?v=1∑3?∣D∣∣Dv∣?Ent(Dv)=1.384?123?×1.585?125?×1.371?124?×0.811=0.146?

2. $AST$

   有两个可能取值 { y e s , n o } \{yes,no\} { yes,no}，对应下标$1,2$
   D 1 = { 2 , 3 , 6 , 7 , 8 , 11 , 12 } p 1 = 0 , p 2 = 3 7 , p 3 = 4 7 E n t ( D 1 ) = ? ( 3 7 log ? 2 3 7 + 4 7 log ? 2 4 7 ) = 0.985 D 2 = { 1 , 4 , 5 , 9 , 10 } p 1 = 2 5 , p 2 = 0 , p 3 = 3 5 E n t ( D 2 ) = ? ( 2 5 log ? 2 2 5 + 3 5 log ? 2 3 5 ) = 0.971 G a i n ( D , A S T ) = E n t ( D ) ? ∑ v = 1 2 ∣ D v ∣ ∣ D ∣ E n t ( D v ) = 1.384 ? 7 12 × 0.985 ? 5 12 × 0.971 = 0.405 \begin{aligned} &D^1=\{2,3,6,7,8,11,12\} \quad p_1=0,\ p_2=\frac{3}{7},\ p_3=\frac{4}{7} \quad Ent(D^1)=-(\frac{3}{7}\log_2{\frac{3}{7}}+\frac{4}{7}\log_2{\frac{4}{7}})=0.985 \\ &D^2=\{1,4,5,9,10\} \quad p_1=\frac{2}{5},\ p_2=0,\ p_3=\frac{3}{5} \quad Ent(D^2)=-(\frac{2}{5}\log_2{\frac{2}{5}}+\frac{3}{5}\log_2{\frac{3}{5}})=0.971 \\ &Gain(D,AST)=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v)=1.384-\frac{7}{12}\times 0.985-\frac{5}{12}\times 0.971=0.405 \end{aligned} ?D1={ 2,3,6,7,8,11,12}p1?=0, p2?=73?, p3?=74?Ent(D1)=?(73?log2?73?+74?log2?74?)=0.985D2={ 1,4,5,9,10}p1?=52?, p2?=0, p3?=53?Ent(D2)=?(52?log2?52?+53?log2?53?)=0.971Gain(D,AST)=Ent(D)?v=1∑2?∣D∣∣Dv∣?Ent(Dv)=1.384?127?×0.985?125?×0.971=0.405?

3. $TEA$

   有两个可能的取值 { n o r m a l , r e d u c e d } \{normal,reduced\} { normal,reduced}，对应下标$1,2$
   D 1 = { 1 , 3 , 5 , 6 , 7 , 8 , 10 , 12 } p 1 = 2 8 , p 2 = 3 8 , p 3 = 3 8 E n t ( D 1 ) = ? ( 2 8 log ? 2 2 8 + 3 8 log ? 2 3 8 + 3 8 log ? 2 3 8 ) = 1.561 D 2 = { 2 , 4 , 9 , 11 } p 1 = 0 , p 2 = 0 , p 3 = 1 E n t ( D 2 ) = ? ( 1 log ? 2 1 ) = 0 G a i n ( D , T E A ) = E n t ( D ) ? ∑ v = 1 2 ∣ D v ∣ ∣ D ∣ E n t ( D v ) = 1.384 ? 8 12 × 1.561 ? 5 12 × 0 = 0.343 \begin{aligned} &D^1=\{1,3,5,6,7,8,10,12\} \quad p_1=\frac{2}{8},\ p_2=\frac{3}{8},\ p_3=\frac{3}{8} \quad Ent(D^1)=-(\frac{2}{8}\log_2{\frac{2}{8}}+\frac{3}{8}\log_2{\frac{3}{8}}+\frac{3}{8}\log_2{\frac{3}{8}})=1.561 \\ &D^2=\{2,4,9,11\} \quad p_1=0,\ p_2=0,\ p_3=1 \quad Ent(D^2)=-(1\log_2{1})=0 \\ &Gain(D,TEA)=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v)=1.384-\frac{8}{12}\times 1.561-\frac{5}{12}\times 0=0.343 \end{aligned} ?D1={ 1,3,5,6,7,8,10,12}p1?=82?, p2?=83?, p3?=83?Ent(D1)=?(82?log2?82?+83?log2?83?+83?log2?83?)=1.561D2={ 2,4,9,11}p1?=0, p2?=0, p3?=1Ent(D2)=?(1log2?1)=0Gain(D,TEA)=Ent(D)?v=1∑2?∣D∣∣Dv∣?Ent(Dv)=1.384?128?×1.561?125?×0=0.343?

于是，$Gain(D,AST)$最大，选它为划分属性，

对左分支节点划分，可用属性集 A = { A G E , T E A } A=\{AGE,TEA\} A={ AGE,TEA}，类别为$CON$。该节点的信息熵$Ent(D^1)=0.985$。计算每个属性的信息熵和信息增益，记$p(soft)=p_1,p(hard)=p_2,p(none)=p_3$，

1. $AGE$

   有三个可能取值 { y o u n g , p r e ? p r e , p r e } \{young,pre-pre,pre\} { young,pre?pre,pre}，对应下标$1,2,3$
   D 11 = { 2 , 3 } p 1 = 0 , p 2 = 1 2 , p 3 = 1 2 E n t ( D 11 ) = ? ( 1 2 log ? 2 1 2 + 1 2 log ? 2 1 2 ) = 1.000 D 12 = { 6 , 7 , 8 } p 1 = 0 , p 2 = 1 3 , p 3 = 2 3 E n t ( D 12 ) = ? ( 1 3 log ? 2 1 3 + 2 3 log ? 2 2 3 ) = 0.918 D 13 = { 11 , 12 } p 1 = 0 , p 2 = 1 2 , p 3 = 1 2 E n t ( D 13 ) = ? ( 1 2 log ? 2 1 2 + 1 2 log ? 2 1 2 ) = 1.000 G a i n ( D 1 , A G E ) = E n t ( D ) ? ∑ v = 1 3 ∣ D 1 v ∣ ∣ D 1 ∣ E n t ( D 1 v ) = 0.985 ? 2 7 × 1.000 ? 3 7 × 0.918 ? 2 7 × 1.000 = 0.020 \begin{aligned} &D^{11}=\{2,3\} \quad p_1=0,\ p_2=\frac{1}{2},\ p_3=\frac{1}{2} \quad Ent(D^{11})=-(\frac{1}{2}\log_2{\frac{1}{2}}+\frac{1}{2}\log_2{\frac{1}{2}})=1.000 \\ &D^{12}=\{6,7,8\} \quad p_1=0,\ p_2=\frac{1}{3},\ p_3=\frac{2}{3} \quad Ent(D^{12})=-(\frac{1}{3}\log_2{\frac{1}{3}}+\frac{2}{3}\log_2{\frac{2}{3}})=0.918 \\ &D^{13}=\{11,12\} \quad p_1=0,\ p_2=\frac{1}{2},\ p_3=\frac{1}{2} \quad Ent(D^{13})=-(\frac{1}{2}\log_2{\frac{1}{2}}+\frac{1}{2}\log_2{\frac{1}{2}})=1.000 \\ &Gain(D^1,AGE)=Ent(D)-\sum_{v=1}^3 \frac{|D^{1v}|}{|D^1|}Ent(D^{1v})=0.985-\frac{2}{7}\times 1.000-\frac{3}{7}\times 0.918-\frac{2}{7}\times 1.000=0.020 \end{aligned} ?D11={ 2,3}p1?=0, p2?=21?, p3?=21?Ent(D11)=?(21?log2?21?+21?log2?21?)=1.000D12={ 6,7,8}p1?=0, p2?=31?, p3?=32?Ent(D12)=?(31?log2?31?+32?log2?32?)=0.918D13={ 11,12}p1?=0, p2?=21?, p3?=21?Ent(D13)=?(21?log2?21?+21?log2?21?)=1.000Gain(D1,AGE)=Ent(D)?v=1∑3?∣D1∣∣D1v∣?Ent(D1v)=0.985?72?×1.000?73?×0.918?72?×1.000=0.020?

2. $TEA$

   有两个可能的取值 { n o r m a l , r e d u c e d } \{normal,reduced\} { normal,reduced}，对应下标$1,2$
   D 11 = { 3 , 6 , 7 , 8 , 12 } p 1 = 0 , p 2 = 3 5 , p 3 = 2 5 E n t ( D 1 ) = ? ( 3 5 log ? 2 3 5 + 2 5 log ? 2 2 5 ) = 0.971 D 12 = { 2 , 11 } p 1 = 0 , p 2 = 0 , p 3 = 1 E n t ( D 2 ) = ? ( 1 log ? 2 1 ) = 0 G a i n ( D 1 , T E A ) = E n t ( D 1 ) ? ∑ v = 1 2 ∣ D 1 v ∣ ∣ D 1 ∣ E n t ( D 1 v ) = 0.985 ? 5 7 × 0.971 ? 2 7 × 0 = 0.291 \begin{aligned} &D^{11}=\{3,6,7,8,12\} \quad p_1=0,\ p_2=\frac{3}{5},\ p_3=\frac{2}{5} \quad Ent(D^1)=-(\frac{3}{5}\log_2{\frac{3}{5}}+\frac{2}{5}\log_2{\frac{2}{5}})=0.971 \\ &D^{12}=\{2,11\} \quad p_1=0,\ p_2=0,\ p_3=1 \quad Ent(D^2)=-(1\log_2{1})=0 \\ &Gain(D^1,TEA)=Ent(D^1)-\sum_{v=1}^2 \frac{|D^{1v}|}{|D^1|}Ent(D^{1v})=0.985-\frac{5}{7}\times 0.971-\frac{2}{7}\times 0=0.291 \end{aligned} ?D11={ 3,6,7,8,12}p1?=0, p2?=53?, p3?=52?Ent(D1)=?(53?log2?53?+52?log2?52?)=0.971D12={ 2,11}p1?=0, p2?=0, p3?=1Ent(D2)=?(1log2?1)=0Gain(D1,TEA)=Ent(D1)?v=1∑2?∣D1∣∣D1v∣?Ent(D1v)=0.985?75?×0.971?72?×0=0.291?

于是，$Gain(D^1,TEA)$最大，选它为划分属性，

继续对左分支节点划分，可用属性集 A = { A G E } A=\{AGE\} A={ AGE}，类别为$CON$。选它为划分属性，得到$D^{111},D^{112},D^{113}$，此时属性集合为空，将这三个节点设为叶子节点，其中$D^{112}$中$p_2=\frac{1}{3},p_3=\frac{2}{3}$，因此将$D^{112}$对应叶子节点标注为$none$类别，其余两个节点中只有一个样本，将叶子节点标记为对应样本类别，返回。考察$D^{12}$，包含样本均属同一类别$none$，则将$D^{12}$标记为$none$。

回到一层，对一层右分支节点划分，可用属性集 A = { A G E , T E A } A=\{AGE,TEA\} A={ AGE,TEA}，类别为$CON$。该节点的信息熵$Ent(D^1)=0.971$。计算每个属性的信息熵和信息增益，记$p(soft)=p_1,p(hard)=p_2,p(none)=p_3$，

1. $AGE$

   有三个可能取值 { y o u n g , p r e ? p r e , p r e } \{young,pre-pre,pre\} { young,pre?pre,pre}，对应下标$1,2,3$
   D 21 = { 1 } p 1 = 1 , p 2 = 0 , p 3 = 0 E n t ( D 11 ) = ? ( 1 log ? 2 1 ) = 0.000 D 22 = { 4 , 5 } p 1 = 0 , p 2 = 1 2 , p 3 = 1 2 E n t ( D 12 ) = ? ( 1 2 log ? 2 1 2 + 1 2 log ? 2 1 2 ) = 1.000 D 23 = { 9 , 10 } p 1 = 0 , p 2 = 0 , p 3 = 1 E n t ( D 13 ) = ? ( 1 log ? 2 1 ) = 0.000 G a i n ( D 2 , A G E ) = E n t ( D 2 ) ? ∑ v = 1 3 ∣ D 2 v ∣ ∣ D 2 ∣ E n t ( D 2 v ) = 0.971 ? 1 5 × 0.000 ? 2 5 × 1.000 ? 2 5 × 0.000 = 0.571 \begin{aligned} &D^{21}=\{1\} \quad p_1=1,\ p_2=0,\ p_3=0 \quad Ent(D^{11})=-(1\log_2 1)=0.000 \\ &D^{22}=\{4,5\} \quad p_1=0,\ p_2=\frac{1}{2},\ p_3=\frac{1}{2} \quad Ent(D^{12})=-(\frac{1}{2}\log_2{\frac{1}{2}}+\frac{1}{2}\log_2{\frac{1}{2}})=1.000 \\ &D^{23}=\{9,10\} \quad p_1=0,\ p_2=0,\ p_3=1 \quad Ent(D^{13})=-(1\log_2{1})=0.000 \\ &Gain(D^2,AGE)=Ent(D^2)-\sum_{v=1}^3 \frac{|D^{2v}|}{|D^2|}Ent(D^{2v})=0.971-\frac{1}{5}\times 0.000-\frac{2}{5}\times 1.000-\frac{2}{5}\times 0.000=0.571 \end{aligned} ?D21={ 1}p1?=1, p2?=0, p3?=0Ent(D11)=?(1log2?1)=0.000D22={ 4,5}p1?=0, p2?=21?, p3?=21?Ent(D12)=?(21?log2?21?+21?log2?21?)=1.000D23={ 9,10}p1?=0, p2?=0, p3?=1Ent(D13)=?(1log2?1)=0.000Gain(D2,AGE)=Ent(D2)?v=1∑3?∣D2∣∣D2v∣?Ent(D2v)=0.971?51?×0.000?52?×1.000?52?×0.000=0.571?

2. $TEA$

   有两个可能的取值 { n o r m a l , r e d u c e d } \{normal,reduced\} { normal,reduced}，对应下标$1,2$
   D 21 = { 1 , 5 , 10 } p 1 = 2 3 , p 2 = 0 , p 3 = 1 3 E n t ( D 1 ) = ? ( 2 3 log ? 2 2 3 + 1 3 log ? 2 1 3 ) = 0.918 D 22 = { 4 , 9 } p 1 = 0 , p 2 = 0 , p 3 = 1 E n t ( D 2 ) = ? ( 1 log ? 2 1 ) = 0 G a i n ( D 2 , T E A ) = E n t ( D 2 ) ? ∑ v = 1 2 ∣ D 2 v ∣ ∣ D 2 ∣ E n t ( D 2 v ) = 0.971 ? 3 5 × 0.918 = 0.420 \begin{aligned} &D^{21}=\{1,5,10\} \quad p_1=\frac{2}{3},\ p_2=0,\ p_3=\frac{1}{3} \quad Ent(D^1)=-(\frac{2}{3}\log_2{\frac{2}{3}}+\frac{1}{3}\log_2{\frac{1}{3}})=0.918 \\ &D^{22}=\{4,9\} \quad p_1=0,\ p_2=0,\ p_3=1 \quad Ent(D^2)=-(1\log_2{1})=0 \\ &Gain(D^2,TEA)=Ent(D^2)-\sum_{v=1}^2 \frac{|D^{2v}|}{|D^2|}Ent(D^{2v})=0.971-\frac{3}{5}\times 0.918=0.420 \end{aligned} ?D21={ 1,5,10}p1?=32?, p2?=0, p3?=31?Ent(D1)=?(32?log2?32?+31?log2?31?)=0.918D22={ 4,9}p1?=0, p2?=0, p3?=1Ent(D2)=?(1log2?1)=0Gain(D2,TEA)=Ent(D2)?v=1∑2?∣D2∣∣D2v∣?Ent(D2v)=0.971?53?×0.918=0.420?

于是，$Gain(D^2,AGE)$最大，选它为划分属性，

考察$D^{21}$，由于只有一个样本，所以直接将$D^{21}$设置为叶子节点，标记为$soft$，返回到$D^{22}$.此时可用的属性集 A = { T E A } A=\{TEA\} A={ TEA}，选它为划分属性，此时属性集为空，将这两个节点设置为叶子节点，这两个叶子节点中都只有一个样本，于是标记为对应样本类别，返回。考察$D^{23}$，其中样本全部属于类别$none$，所以直接将$D^{23}$设置为叶子节点，标记为$none$。最终得到决策树