算法提高 最小方差生成树（枚举 + Kruskal）

试题 算法提高 最小方差生成树

资源限制
时间限制：1.0s 内存限制：256.0MB
问题描述
给定带权无向图，求出一颗方差最小的生成树。
输入格式
输入多组测试数据。第一行为N,M，依次是点数和边数。接下来M行，每行三个整数U,V,W，代表连接U,V的边，和权值W。保证图连通。n=m=0标志着测试文件的结束。
输出格式
对于每组数据，输出最小方差，四舍五入到0.01。输出格式按照样例。
样例输入
4 5
1 2 1
2 3 2
3 4 2
4 1 1
2 4 3
4 6
1 2 1
2 3 2
3 4 3
4 1 1
2 4 3
1 3 3
0 0
样例输出
Case 1: 0.22
Case 2: 0.00
数据规模与约定
1<=U,V<=N<=50,N-1<=M<=1000,0<=W<=50。数据不超过5组。

题解
最小方差树的概念就是，在n个结点的图中，挑n-1个边，首先要使这个图连通，然后，这n-1条边的权值的方差要最小，方差的计算公式为：

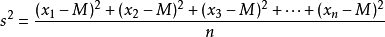
可以看出，方差与边的平均值有关，但是有一个难点是，随着边的加入，边的平均值会动态地变化，很不利于解题。
这里有一个思路：在总的边的权和已知的情况下求解最小的方差，这是容易实现的，因为边权总和已知，然后结点数量(n)已知的话，边的数量也就知道了(n-1)，这样边的平均值就知道了，这样各条边与均值的平方就是一个不动的常数了。此时我们再求最小生成树的过程中，边的权值就不是原来的权值了，而是其权值与平均值差值的平方，然后按照最小生成树的步骤求出最小的方差树。
AC代码如下：使用克鲁斯卡尔算法求MST，使用到了并查集，代码来自https://www.cnblogs.com/asuml/p/6798307.html

#include <cstdio>
#include <algorithm>
using namespace std;double const MAX = 10000000000000.0;
int n, m, tmp[1005], fa[55];
double ans;struct Edge
{
    int u, v;double w, val;
}e[1005];bool cmp(Edge a, Edge b)
{
    return a.w < b.w;
}void UF_set(int n)
{
    for(int i = 1; i <= n; i++)fa[i] = i;
}int Find(int x)
{
    return x == fa[x] ? x : fa[x] = Find(fa[x]);
}void Union(int a, int b)
{
    int r1 = Find(a);int r2 = Find(b);if(r1 != r2)fa[r2] = r1;
}void Kruskal(int sum)
{
    UF_set(n);int cnt = 0;double f_all = 0;double all = 0;double ave = sum * 1.0 / (n - 1);for(int i = 0; i < m; i++)e[i].w = (e[i].val - ave) * (e[i].val - ave);sort(e, e + m, cmp);for(int i = 0; i < m; i++){
    int u = e[i].u;int v = e[i].v;if(Find(u) != Find(v)){
    Union(u, v);f_all += e[i].w;all += e[i].val;cnt ++;}if(cnt == n - 1)break;}if((int)all == sum)ans = min(ans, f_all);
}int main()
{
    int ca = 1;while(scanf("%d %d", &n, &m) != EOF && (m + n)){
    // if(n == 1 || n == 2)// {
    // printf("0.00\n");// continue;// }int minv = 0;int maxv = 0;ans = MAX;for(int i = 0; i < m; i++){
    scanf("%d %d %lf", &e[i].u, &e[i].v, &e[i].val);tmp[i] = e[i].val;}sort(tmp, tmp + m);for(int i = 0; i < n - 1; i++)minv += tmp[i];for(int i = m - 1; i > m - n; i--)maxv += tmp[i];for(int i = minv; i <= maxv; i++)Kruskal(i);ans = ans / (n - 1);printf("Case %d: %.2f\n", ca++, ans);}
}

可以看出，先按边的权值从大到小枚举，然后取其中n-1条边，这n-1条边的最大值就是从后往前取，最小值是从前往后取，然后最小生成树的代价就会在这两者之间，一一枚举，如果找到了有这样一个MST，那么求该情况下最小的方差，最后在所有可能的方差中取最小的。

PS。编者有一个做法，没有AC，功能上不大对，还是想与大家分享：
先选定一个点(a)，用其一条边作为出发边，然后使用Prim算法求最小生成树，配合优先队列，每次从队列取边的时候，更新目前选定边的均值，然后每次从队列拿出的是与均值差最小的边，直到访问所有结点。这样还需要从a的其他边出发遍历，因为不知道是哪一条边构成的MST，但是肯定有一条边是属于MST的，不然结点a就孤立了。然后取这几种情况中方差的最小值。
代码如下：

#include<bits/stdc++.h>
using namespace std;struct edge {
    int from;int to;int we;edge(int _from = 0, int _to = 0, int _we = 0) {
     from = _from; to = _to; we = _we; }
};
vector<edge> V[51];
vector<edge> choose;
bool vis[51];
int N, M;
float fenzi, fenmu, shang;
float ans;struct cmp {
    bool operator()(edge a, edge b) {
    return  abs(a.we - shang) > abs(b.we - shang);}
};void prim() {
    ans = 1e6;for (int i = 0; i < V[1].size(); i++) {
    priority_queue<edge, vector<edge>, cmp > Q;memset(vis, 0, sizeof(vis));fenzi = 0;fenmu = 0;choose.clear();int code = 1;Q.push(V[1][i]);vis[1] = 1;while (!Q.empty()) {
    edge tmp = Q.top();Q.pop();if (code) {
    code = 0;for (int j = 0; j < V[1].size(); j++)if (j != i)Q.push(V[1][j]);}if (vis[tmp.to])continue;vis[tmp.to] = 1;choose.push_back(tmp);fenmu++;fenzi += tmp.we;shang = fenzi / fenmu;for (int j = 0; j < V[tmp.to].size(); j++) {
    Q.push(V[tmp.to][j]);}}float h = 0;for (int j = 0; j < choose.size(); j++) {
    h += (choose[j].we - shang)*(choose[j].we - shang);}ans = min(ans, h / fenmu);}
}int main() {
    int a, b, c;int ccase = 0;while (scanf("%d%d", &N, &M) && N&&M) {
    ccase++;for (int i = 0; i < 51; i++)V[i].clear();for (int i = 0; i < M; i++) {
    scanf("%d%d%d", &a, &b, &c);V[a].push_back(edge(a, b, c));V[b].push_back(edge(b, a, c));}prim();printf("Case %d: %.2f\n", ccase, ans);}return 0;
}