OpenCV4 详解仿射变换和透视变换和C++实现

作者：RayChiu_Labloy
版权声明：著作权归作者所有，商业转载请联系作者获得授权，非商业转载请注明出处

---

目录

 2D图像变换包括：

仿射变换和透视变换区别：

 仿射变换：

 使用场景：

原理： 

平移、旋转、缩放和翻转等对应的仿射变换矩阵：

平移：

 旋转：

 翻转:

 缩放：

 刚体变换：

 相似变换：

 总结：

相关函数：

C++ 实现： 

 透视(投影)变换：

 使用场景：

 原理：

 相关函数：

C++实现：

python实现仿射变换和透视变换：

---

 2D图像变换包括：

1. 基于2×3矩阵的仿射变换
2. 基于3×3矩阵透视变换

仿射变换和透视变换区别：

        仿射变换后平行四边形的各边仍操持平行，透视变换结果允许是梯形等四边形，所以仿射变换是透视变换的子集 

 仿射变换：

 使用场景：

1. 平移
2. 旋转
3. 缩放
4. 错切（类似矩形变平行四边形）
5. 翻转 

原理： 

其实就是二维坐标的变换：从一种二维坐标(x,y)到另一种二维坐标(u,v)的线性变换：  

如果写成矩阵的形式，就是： 

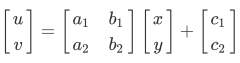
任意的仿射变换都能表示为乘以一个矩阵(线性变换)，再加上一个向量 (平移) 的形式． 

我们作如下定义：

平移、旋转、缩放和翻转等对应的仿射变换矩阵：

平移：

 平移就是x和y方向上的直接移动，可以上下 ty /左右 tx 移动，自由度为2，变换矩阵可以表示为：

 旋转：

旋转是坐标轴方向饶原点旋转一定的角度θ，自由度为1，不包含平移，如顺时针旋转可以表示为：

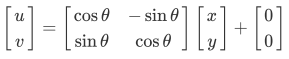
 翻转:

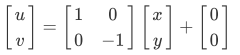
 缩放：

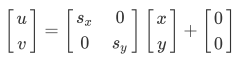
 刚体变换：

就是平移、旋转和翻转的组合，图像变换前后两点间的距离仍然保持不变，自由度为3（夹角、tx、ty）。变换矩阵可以表示为：

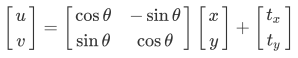
 相似变换：

 就是刚体变换的基础上加了缩放，所以并不会保持欧氏距离不变，但直线间的夹角依然不变。自由度为4（缩放比例、旋转角度、x和y向平移量）。若缩放比例为scale，旋转角度为θ，旋转中心是$ (center_x,center_y) $，则仿射变换可以表示为：

 其中：

 总结：

相关函数：

cvWrapAffine(src,dst,mat) 

C++ 实现： 

//仿射变换—平移，旋转，缩放，翻转，错切#include "stdafx.h"
#include<opencv2/opencv.hpp>
#include<iostream>
#include<math.h>using namespace cv;
using namespace std;int main(int argc, char* argv) {Mat src, dst;src = imread("C:/Users/59235/Desktop/image/girl5.jpg");if (!src.data) {printf("could not load image...\n");return -1;}namedWindow("original image", CV_WINDOW_AUTOSIZE);imshow("original image", src);Mat dst_warp, dst_warpRotateScale, dst_warpTransformation, dst_warpFlip;Point2f srcPoints[3];//原图中的三点 ,一个包含三维点（x，y）的数组，其中x、y是浮点型数Point2f dstPoints[3];//目标图中的三点  //第一种仿射变换的调用方式：三点法//三个点对的值,上面也说了，只要知道你想要变换后图的三个点的坐标，就可以实现仿射变换  srcPoints[0] = Point2f(0, 0);srcPoints[1] = Point2f(0, src.rows);srcPoints[2] = Point2f(src.cols, 0);//映射后的三个坐标值dstPoints[0] = Point2f(0, src.rows*0.3);dstPoints[1] = Point2f(src.cols*0.25, src.rows*0.75);dstPoints[2] = Point2f(src.cols*0.75, src.rows*0.25);Mat M1 = getAffineTransform(srcPoints, dstPoints);//由三个点对计算变换矩阵  warpAffine(src, dst_warp, M1, src.size());//仿射变换  //第二种仿射变换的调用方式：直接指定角度和比例                                          //旋转加缩放  Point2f center(src.cols / 2, src.rows / 2);//旋转中心  double angle = 45;//逆时针旋转45度  double scale = 0.5;//缩放比例  Mat M2 = getRotationMatrix2D(center, angle, scale);//计算旋转加缩放的变换矩阵  warpAffine(src, dst_warpRotateScale, M2, Size(src.cols, src.rows), INTER_LINEAR);//仿射变换//仿射变换—平移Point2f srcPoints1[3];Point2f dstPoints1[3];srcPoints1[0] = Point2i(0, 0);srcPoints1[1] = Point2i(0, src.rows);srcPoints1[2] = Point2i(src.cols, 0);dstPoints1[0] = Point2i(src.cols / 3, 0);dstPoints1[1] = Point2i(src.cols / 3, src.rows);dstPoints1[2] = Point2i(src.cols + src.cols / 3, 0);Mat M3 = getAffineTransform(srcPoints1, dstPoints1);warpAffine(src, dst_warpTransformation, M3, Size(src.cols + src.cols / 3, src.rows));//仿射变换—翻转、镜像Point2f srcPoints2[3];Point2f dstPoints2[3];srcPoints2[0] = Point2i(0, 0);srcPoints2[1] = Point2i(0, src.rows);srcPoints2[2] = Point2i(src.cols, 0);dstPoints2[0] = Point2i(src.cols, 0);dstPoints2[1] = Point2i(src.cols, src.rows);dstPoints2[2] = Point2i(0, 0);Mat M4 = getAffineTransform(srcPoints2, dstPoints2);warpAffine(src, dst_warpFlip, M4, Size(src.cols, src.rows));//flip(src, dst_warpFlip, 1);//  flipCode：= 0 图像向下翻转//> 0 图像向右翻转//< 0 图像同时向下向右翻转imshow("affine transformation1（三点法）", dst_warp);imshow("affine transfoemation2（指定比例和角度）", dst_warpRotateScale);imshow("affine transfoemation3（仿射变换平移）", dst_warpTransformation);imshow("affine transformation4(仿射变换镜像)", dst_warpFlip);waitKey(0);return 0;
}

 透视(投影)变换：

 使用场景：

        将2D矩阵图像变换成3D的空间显示效果，全景拼接 。

 原理：

         前面仿射变换后依然是平行四边形，并不能做到任意的变换。

        透视变换（Perspective Transformation）是将二维的图片投影到一个三维视平面上，然后再转换到二维坐标下，所以也称为投影映射（Projective Mapping）。简单来说就是 二维(x,y) →三维(X,Y,Z)→二维(x’,y’) 的一个过程。

 齐次矩阵的形式：

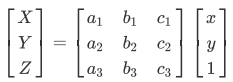
 其中a1、b1、a2、b2表示线性变换，a3、b3产生透视变换，c1、c2、c3是平移变换。

 接下来再通过除以Z轴转换成二维坐标：

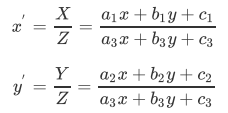
        透视变换相比仿射变换更加灵活，变换后会产生一个新的四边形，但不一定是平行四边形，所以需要非共线的四个点才能唯一确定，原图中的直线变换后依然是直线。因为四边形包括了所有的平行四边形，所以透视变换包括了所有的仿射变换。

 相关函数：

 cvWrapPerspective(src,dst,mat)

C++实现：

#include <iostream>
#include <opencv.hpp>
using namespace std;
using namespace cv;Mat PerspectiveTrans(Mat src, Point2f* scrPoints, Point2f* dstPoints)
{Mat dst;Mat Trans = getPerspectiveTransform(scrPoints, dstPoints);warpPerspective(src, dst, Trans, Size(src.cols, src.rows), CV_INTER_CUBIC);return dst;
}void main()
{Mat I = imread("1.jpg");	//700*438Point2f AffinePoints0[4] = { Point2f(100, 50), Point2f(100, 390), Point2f(600, 50), Point2f(600, 390) };Point2f AffinePoints1[4] = { Point2f(200, 100), Point2f(200, 330), Point2f(500, 50), Point2f(600, 390) };Mat dst_perspective = PerspectiveTrans(I, AffinePoints0, AffinePoints1);for (int i = 0; i < 4; i++){circle(I, AffinePoints0[i], 2, Scalar(0, 0, 255), 2);circle(dst_perspective, AffinePoints1[i], 2, Scalar(0, 0, 255), 2);}imshow("origin", I);imshow("perspective", dst_perspective);waitKey();
}

 效果：

python实现仿射变换和透视变换：

请看我的另外一篇文章：opencv-python 实现仿射变换和透视变换_RayChiu757374816的博客-CSDN博客

【如果对您有帮助，交个朋友给个一键三连吧，您的肯定是我博客高质量维护的动力！！！】