jieba 分词源代码研读(3)_综合

前面两篇文章说到了根据语料库和频度打分机制生成一个初步的分词结果。但是我们的分词结果仅仅用到了语料库已有的词语和频度，所以对于语料库中没有出现的词语判断能力等于0，比如下面这句：

'乔治马丁写冰与火之歌拖了好久'

其分词结果如下：

{0: (-99.10570994217552, 1), 1: (-95.82849854029436, 1), 2: (-86.8396051928814, 3), 3: (-84.72890670707343, 3), 4: (-75.00798674103962, 4), 5: (-66.83881448624362, 5), 6: (-56.61112681956269, 6), 7: (-50.688635432771534, 7), 8: (-41.82702063631733, 8), 9: (-35.77167914769012, 9), 10: (-25.879411293669556, 10), 11: (-16.115147905438818, 11), 12: (-11.89539448723901, 13), 13: (-8.9697445285742, 13), 14: (0.0, '')}

'乔治/马丁/写/冰/与/火/之/歌/拖/了/好久'

其中 “冰与火之歌" 没有在语料库里出现过，所以没有被识别出来的（注意没有在语料库里出现过的词通常称作未登录词，而初步的分词会把未登录词一个字一个字的”切割“开）。那么应该怎么样改进呢？

回到 __cut_DAG 函数，这个函数前半部分用 calc 函数计算出了初步的分词，而后半部分就是就是针对上面例子中未出现在语料库的词语进行分词了。后半部分代码如下：

    x = 0buf =u''N = len(sentence)while x<N:y = route[x][1]+1l_word = sentence[x:y]if y-x==1:buf+= l_wordelse:if len(buf)>0:if len(buf)==1:yield bufbuf=u''else:if (buf not in FREQ):regognized = finalseg.cut(buf)for t in regognized:yield telse:for elem in buf:yield elembuf=u''yield l_wordx =y

由于基于频度打分的分词会倾向于把不能识别的词组一个字一个字地切割开，所以对这些字的归并就是识别未知词语并且优化分词结果的一个方向。在代码中，定义了一个buf 变量收集了这些连续的单个字，把它们组合成字符串再交由 finalseg.cut 函数来进行下一步分词。

该函数封装在finalseg模块中，主要通过 __cut 函数来进行进一步的分词。代码如下：

def __cut(sentence):global emit_Pprob, pos_list =  viterbi(sentence,('B','M','E','S'), start_P, trans_P, emit_P)begin, next = 0,0#print pos_list, sentencefor i,char in enumerate(sentence):pos = pos_list[i]if pos=='B':begin = ielif pos=='E':yield sentence[begin:i+1]next = i+1elif pos=='S':yield charnext = i+1if next<len(sentence):yield sentence[next:]

要理解这段代码，必须先掌握一些相关的数学知识，因为这里使用了隐含马尔科夫模型（HMM）和维特比算法（Viterbi）。

在HMM中有两种状态，一种是具有决定性的隐含着的状态(简称状态)，另一种的显性输出的状态(简称输出)。在结巴分词中状态有4种，分别是B,M,E,S，对应于一个汉字在词语中的地位即B（开头）,M（中间 ),E（结尾）,S（独立成词），而输出就是一个汉字。

在HMM中还有三种状态分别是状态分布概率，状态转移概率和发射概率（发射概率是一个条件概率，表示在某一状态下得到某一输出的概率）。

现在我们的情况是已经得到了 sentence，即一串输出，而想要知道的是这串汉字最有可能的BMES组合形式，从而进行分词。这就需要使用到维特比算法了。

在结巴分词中作者经过大量的实验在prob_start.py,prob_trans.py,prob_emit.py 中预存好了汉语的一些概率值。prob_start.py 中预存了每种状态的概率，代码如下：

P={'B': -0.26268660809250016,'E': -3.14e+100,'M': -3.14e+100,'S': -1.4652633398537678}

prob_ trans .py中预存了状态将的转移概率，代码如下：

P={'B': {'E': -0.510825623765990, 'M': -0.916290731874155},'E': {'B': -0.5897149736854513, 'S': -0.8085250474669937},'M': {'E': -0.33344856811948514, 'M': -1.2603623820268226},'S': {'B': -0.7211965654669841, 'S': -0.6658631448798212}}

prob_emit.py中预存了在每种状态下输出（汉字）的发射概率。所有的概率值为了防止0的出现，都做了对数变换，0概率表示成了 -3.14e+100(-3.14*e^100，接近负无穷)

对于一个sentence，第一个汉字的状态概率称为初始概率，可以用贝叶斯公式得到：

P(i)*P(k/i)=P(k)*P(i/k)

其中P(i)表示状态的概率,在文件prob_start.py 中可以找到，P(k/i)即发射概率（保存在prob_emit.py），而P(k)即某个汉字出现的概率，忽略不计。则有：

P(i/k)=P(i)*P(k/i)

根据这个公式就有了sentence第一个字的状态的概率值。那么第二个字的状态概率就是：

P(i2) = P(i1)*P(i2 | i1)*P(i2 | k2)*P(k2)÷P(i2) = P(i1)*P(i2 | i1)*P(k2 | i2)

其中P(i1)表示第一个字的状态概率，P(i2)表示第二个字的状态概率，P(i2 | i1)表示状态i1到i2的转移概率，P(k2 | i2)表示发射概率。

以此类推，由于每一个状态都有4种选择（BMES），所以根据每种选择导致的状态转移路径计算得出的概率值也不同，维特比算法的目的就在于找出概率最大的一种转移路径。比如sentence的长度为2（两个汉字），那么算法的目的就是使上面的P(i2) 最大化。那么维特比算法的特点是什么呢？其实到达某一种中间状态的路径有很多条，比如在第三个节点到达状态M，可能路径有 S->B->M，也可以是B->M->M，维特比算法会在中间这一步中就进行”剪枝“，它只记住路径中概率较大的那一条路径，而概率较小的忽略不计，所以只用记住到达这个节点的一条路径就行了。

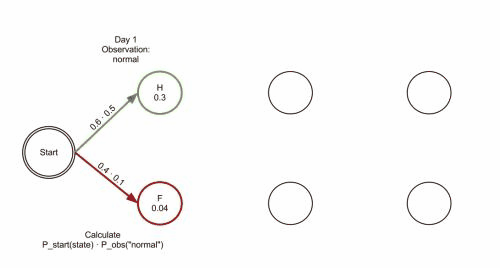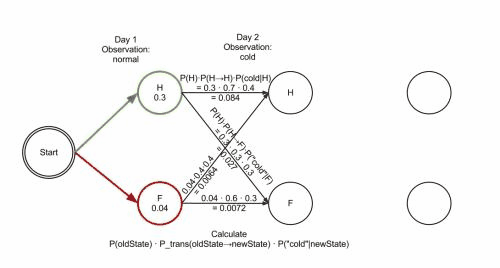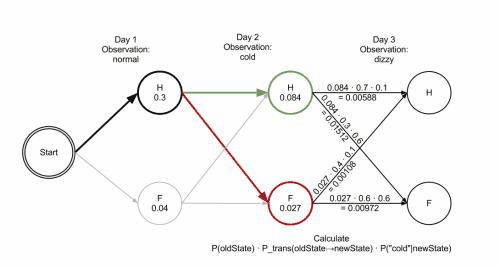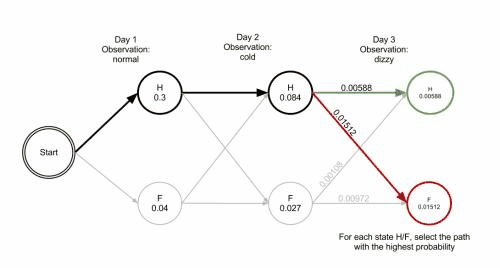
维基百科里有一张 gif图很好地说明了这种剪枝手段：

结巴分词中维特比算法：

#状态转移矩阵，比如B状态前只可能是E或S状态
PrevStatus = {'B':('E','S'),'M':('M','B'),'S':('S','E'),'E':('B','M')
}def viterbi(obs, states, start_p, trans_p, emit_p):V = [{}] #状态概率矩阵path = {}for y in states: V[0][y] = start_p[y] + emit_p[y].get(obs[0],MIN_FLOAT)#计算初始状态概率，由于概率值做了对数化，所以乘号变成了加号path[y] = [y]for t in range(1,len(obs)):V.append({})newpath = {}for y in states:em_p = emit_p[y].get(obs[t],MIN_FLOAT)(prob,state ) = max([(V[t-1][y0] + trans_p[y0].get(y,MIN_FLOAT) + em_p ,y0) for y0 in PrevStatus[y] ])V[t][y] =probnewpath[y] = path[state] + [y]#剪枝，只保存概率最大的一种路径path = newpath(prob, state) = max([(V[len(obs) - 1][y], y) for y in ('E','S')])#求出最后一个字哪一种状态的对应概率最大，最后一个字只可能是两种情况：E(结尾)和S(独立词)return (prob, path[state])

在得到了 BMES 划分后，__cut再进行分词，至此结巴分词的所有奥秘就展现无遗了。

参考连接：

http://hi.baidu.com/hehehehello/item/5ae1ede84422feadcf2d4f71

http://zh.wikipedia.org/wiki/%E7%BB%B4%E7%89%B9%E6%AF%94%E7%AE%97%E6%B3%95

http://blog.csdn.net/hellonlp/article/details/7852904