PAT甲级1045
题目
题意
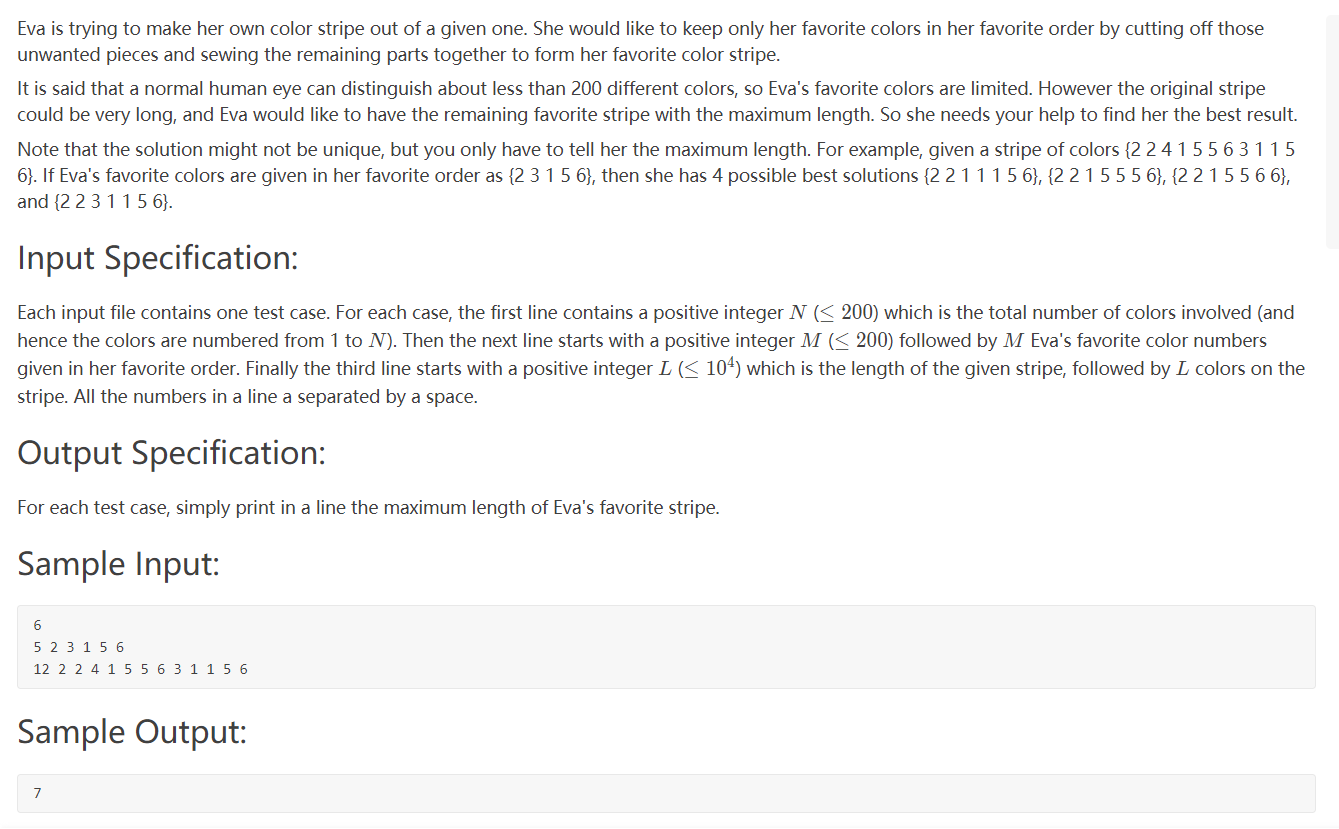
第一行给定一个n表示总颜色数,颜色种类用1 ~ n数字表示
第二行第一个数是Eva喜欢的颜色数m,后面m个数代表Eva喜欢的颜色序列
第三行第一个数是彩带的长度L,后面L个数代表彩带上的颜色序列
我们要做的就是找出在彩带上符合Eva喜欢的颜色序列(符合顺序即可,可以缺少)的最大长度,例如Eva喜欢的颜色序列是{2, 3, 1, 5, 6},彩带序列是{ 2, 2, 4, 1, 5, 5, 6, 3, 1, 1, 5, 6},输出就是7
思路(LIS)
为了符合LIS的思路,我们可以先将数组m中的元素按顺序映射一个为一个递增序列hashTable,比如按题目的样例
m |
2 | 3 | 1 | 5 | 6 |
|---|---|---|---|---|---|
hashTable |
1 | 2 | 3 | 4 | 5 |
对于彩带序列L按照m-hashTable进行映射,m中没有的元素一律设为-1,得到序列ML,同理
L |
2 | 2 | 4 | 1 | 5 | 5 | 6 | 3 | 1 | 1 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
ML |
1 | 1 | -1 | 3 | 4 | 4 | 5 | 2 | 3 | 3 | 4 | 5 |
于是,我们的任务就转化成了求ML的LIS,由于此题的数据较小,套用简单的O(n2)dp模板即可解决,实在不清楚请先学习基本的LIS
CPP代码
#include <bits/stdc++.h>
using namespace::std;
const int maxc = 205;
const int maxL = 1e4 + 5;
int m[maxc], L[maxL], hashTable[maxc], ML[maxL], dp[maxL];
int main()
{
//输入部分int n;cin >> n;int M;cin >> M;for(int i = 1; i <= M; ++i)cin >> m[i];int l;cin >> l;for(int i = 1; i <= l; ++i)cin >> L[i];//建立hash,得出MLfill(hashTable, hashTable + maxc, -1);for(int i = 1; i <= M; ++i)hashTable[m[i]] = i;for(int i = 1; i <= l; ++i)ML[i] = hashTable[L[i]];//对ML进行求LIS,dp方法for(int i = 1; i <= l; ++i){
if(ML[i] < 0)continue;dp[i] = 1;for(int j = 1; j < i; ++j){
if(ML[j] < 0)continue;if(ML[j] <= ML[i])dp[i] = max(dp[i], dp[j] + 1);}}//求得的dp数组中的最大值即题解sort(dp + 1, dp + l + 1);cout << dp[l];return 0;
}
**dp**求LIS方面,和模板唯一的不同是需要在循环进行操作前我们要确保ML[i]是正整数,因为我们将Eva不喜欢的颜色都对应为-1,-1对实际对我们求得的dp数组不应有影响,如果不加判断,当整条彩带没有Eva喜欢的颜色时,居然会返回该彩带的整个长度({-1,-1,-1,-1,…}本身是非降序列);当然,我们也可以直接把不喜欢的颜色排除在ML外