降维算法（LASSO、PCA、聚类分析、小波分析、线性判别分析、拉普拉斯特征映射、局部线性嵌入）_综合

1、LASSO

LASSO全称least absolute shrinkage and selection operator，本身是一种回归方法。与常规回归方法不同的是，LASSO可以对通过参数缩减对参数进行选择，从而达到降维的目的。说到LASSO，就不得不说岭回归，因为LASSO就是针对岭回归不能做参数选择的问题提出来的。关于岭回归的解释，可以参照我的另一篇文章预测数值型数据：回归（二），这里不再赘述。

值得说明的是，岭回归的优化目标函数为 $min_w\sum_{i=0}^n(y_i-x_i^T\theta)^2+\lambda||\theta||_2$ ，最后的惩罚项为二范数，随着 $\lambda$ 的增大，参数慢慢缩减，不过无法缩减到0，也就无法达到参数选择的目的。

LASSO的优化目标函数为 $min_w\sum_{i=0}^n(y_i-x_i^T\theta)^2+\lambda||\theta||_1$ ，惩罚项为一范数，可以将一些参数逼为0，从而达到参数选择的目的，换句话说，实现了特征的降维。引用知乎用户“威廉姆斯YD”的回答，岭回归与LASSO的惩罚项的区别可以直观的由下图表示：

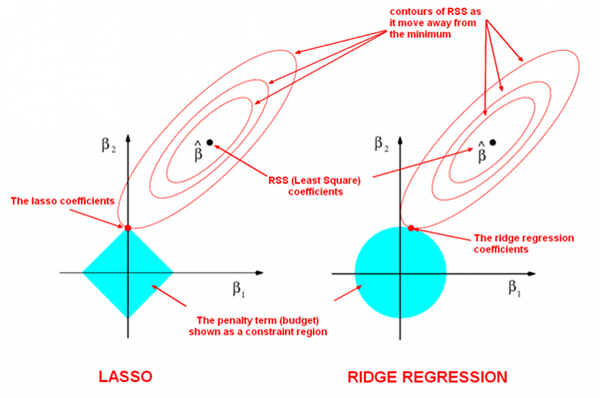
不难看出由于一范数规定的范围四四方方，所以最优解的系数会刚好被缩减为0，因此LASSO可以实现对变量的选择。

2、主成分分析

关于PCA的解释，可以参照我的另一篇文章PCA主成分分析，这里不再赘述。

3、聚类分析

大家所熟知的聚类分析算法如K-means等是一种面对小数据的无监督学习算法，可有效解决低维数据空间的聚类问题。然而在处理高维数据和大型数据等情况时，传统聚类方法往往会失效，这是由于高位数据及中常常存在很多冗余属性且数据在高维分布非常稀疏，距离函数失效。为了解决高维度数据的聚类问题，学术界提出了一种名为高维聚类的算法，具体分为基于属性约减（降维）的方法、基于子空间的方法等。其思想大概是通过特征选择或者特征变换等方法将原始数据集从高维空间转换到低维空间，再利用传统聚类的思想进行聚类。

4、小波分析

小波分析的实质就是将原始信号表示为一组小波基的线性组合。我们可以通过忽略其中不重要的部分来达到降维的目的。
这种思想具体可以用傅里叶变换进行类比。傅里叶变换用不同频率的三角函数的和去拟合原始信号，对于每个单独的三角函数，只需要记录其相位和幅度即可，同时，利用相位和幅度可以完美的重构出原始信号。另外，由于高频分量往往是信号中的噪音，通过去除高频分量可以达到降维的目的。

5、线性判别分析

关于LDA的解释，可以参照我的另一篇文章线性判别分析LDA（Linear Discriminant Analysis），这里不再赘述。

6、拉普拉斯特征映射

关于拉普拉斯特征映射的解释，可以参照我的另一篇文章拉普拉斯特征映射（Laplacian Eigenmaps），这里不再赘述。

7、局部线性嵌入

关于拉普拉斯特征映射的解释，可以参照我的另一篇文章局部线性嵌入（LLE），这里不再赘述。