poj 1061 青蛙的约会数论、扩展欧几里德_综合

青蛙的约会

Description

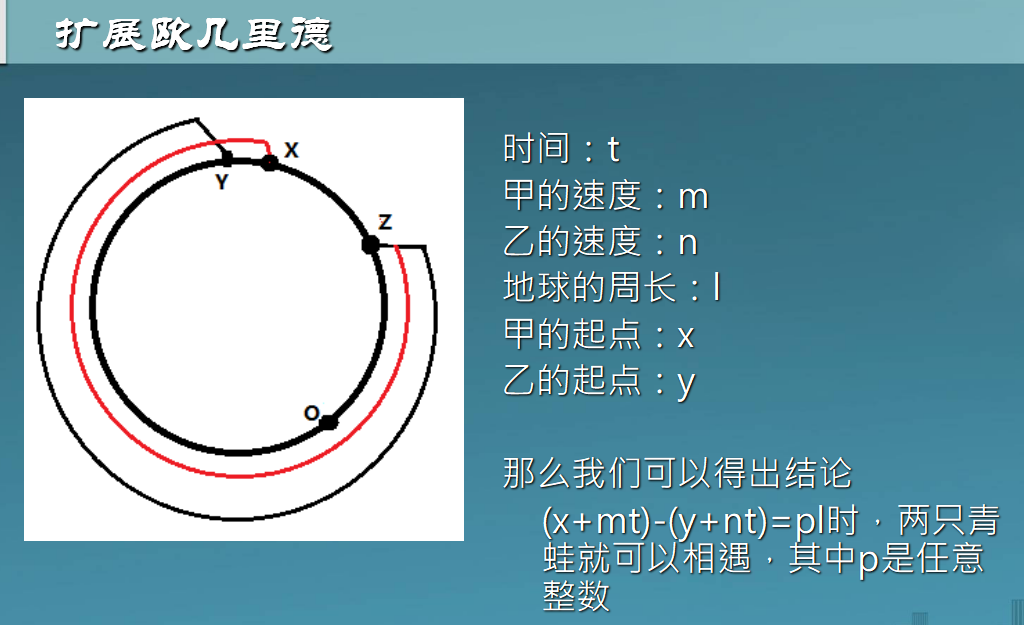
两只青蛙在网上相识了，它们聊得很开心，于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上，于是它们约定各自朝西跳，直到碰面为止。可是它们出发之前忘记了一件很重要的事情，既没有问清楚对方的特征，也没有约定见面的具体位置。不过青蛙们都是很乐观的，它们觉得只要一直朝着某个方向跳下去，总能碰到对方的。但是除非这两只青蛙在同一时间跳到同一点上，不然是永远都不可能碰面的。为了帮助这两只乐观的青蛙，你被要求写一个程序来判断这两只青蛙是否能够碰面，会在什么时候碰面。
我们把这两只青蛙分别叫做青蛙A和青蛙B，并且规定纬度线上东经0度处为原点，由东往西为正方向，单位长度1米，这样我们就得到了一条首尾相接的数轴。设青蛙A的出发点坐标是x，青蛙B的出发点坐标是y。青蛙A一次能跳m米，青蛙B一次能跳n米，两只青蛙跳一次所花费的时间相同。纬度线总长L米。现在要你求出它们跳了几次以后才会碰面。

Input

输入只包括一行5个整数x，y，m，n，L，其中x≠y < 2000000000，0 < m、n < 2000000000，0 < L < 2100000000。

Output

输出碰面所需要的跳跃次数，如果永远不可能碰面则输出一行"Impossible"

Sample Input

1 2 3 4 5

Sample Output

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
long long t,p;
long long euclid(long long a,long long b)
{
if(b==0)
return a;
else
return euclid(b,a%b);
}//辗转相除法
void extended_euclid(long long a,long long b)
{
if(b==0)
{
t=1;
p=0;
}
else
{
long long it;
extended_euclid(b,a%b);
it=t-a/b*p;
t=p;
p=it;
}
}
int main()
{
long long x,y,m,n,L,gcd;
cin>>x>>y>>m>>n>>L;
if(m==n)
{
cout<<"Impossible"<<endl;
return 0;
}
long long a,b,c,c1;
a=n-m;
b=L;
c=x-y;
gcd=euclid(a,b);
c1=c%gcd;
if(c1!=0)
{
cout<<"Impossible"<<endl;
return 0;
}
c/=gcd;
a/=gcd;
b/=gcd;
extended_euclid(a,b);
t*=c;
p*=c;
t=(t%b+b)%b;
cout<<t<<endl;
return 0;

}

数论这个东西。。。全是听老师上课讲的，听得云里雾里的，自己本身其实不是特别深入了解。。。但是顺着推导过程感觉一切还是挺自然的。。。附几张图解吧（参考网上的图片）

poj 1061 青蛙的约会 数论、扩展欧几里德

poj 1061 青蛙的约会数论、扩展欧几里德