Dijkstra算法是处理单源最短路径的有效算法，但它局限于边的权值非负的情况，若图中出现权值为负的边，Dijkstra算法可能就会失效，求出的最短路径就可能是错的。这时候，就需要使用Bellman-Ford算法来求解最短路径，Bellman-Ford算法的流程如下：
给定图G(V, E)（其中V、E分别为图G的顶点集与边集），源点s，
1.数组Distant[i]记录从源点s到顶点i的路径长度，初始化数组Distant[n]为, Distant[s]为0；
2.以下操作循环执行至多n-1次，n为顶点数：
对于每一条边e(u, v)，如果Distant[u] + w(u, v) < Distant[v]，则另Distant[v] = Distant[u]+w(u, v)。w(u, v)为边e(u,v)的权值；
若上述操作没有对Distant进行更新，说明最短路径已经查找完毕，或者部分点不可达，跳出循环。否则执行下次循环；
3.为了检测图中是否存在负环路，即权值之和小于0的环路。对于每一条边e(u, v)，如果存在Distant[u] + w(u, v) < Distant[v]的边，则图中存在负环路，即是说改图无法求出单源最短路径。否则数组Distant[n]中记录的就是源点s到各顶点的最短路径长度。
可知，Bellman-Ford算法寻找单源最短路径的时间复杂度为O(V*E).
介绍一下松弛操作
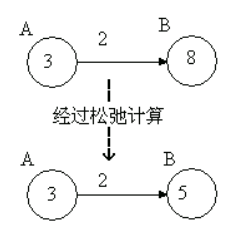Distant[B]>Distant[A]+w(A,B),松弛完成，权值变为2
那如果是这种情况，如下图：
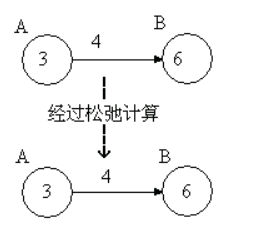
Distant[B]<Distant[A]+w(A,B)，那就不需要松弛了
Bellman－Ford算法可以大致分为三个部分
第一，初始化所有点。每一个点保存一个值，表示从原点到达这个点的距离，将原点的值设为0，其它的点的值设为无穷大（表示不可达）。
第二，进行循环，循环下标为从1到n－1（n等于图中点的个数）。在循环内部，遍历所有的边，进行松弛计算。
第三，遍历途中所有的边（edge（u，v）），判断是否存在这样情况：d（v） > d (u) + w(u,v)，存在则返回false，表示途中存在从源点可达的权为负的回路。
之所以需要第三部分，是因为，如果存在从源点可达的权为负的回路。则应为无法收敛而导致不能求出最短路径。
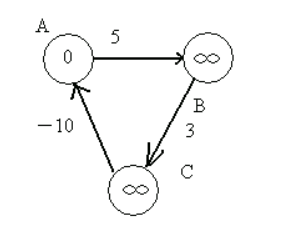
第一次遍历后，Distant[B]=5,Distant[C]=8,但注意接下来这个负权值的边，导致Distant[A]=-2
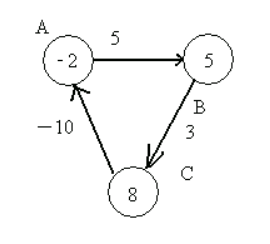
第二次遍历后，Distant[B]=3,Distant[C]=6,Distant[A]=-4,开始出现矛盾循环了，正是因为图中存在一条负权值回路，导致每次遍历，各点值都在减少
所以我们就可以在第三部分检查是否存在可松弛机会（即d（v） > d (u) + w(u,v)），如果存在无法收敛的情况，则肯定可以检查出来
所以，Bellman－Ford算法可以解决图中有权为负数的边的单源最短路径问题。
上代码，方便以后查阅
#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 1005const int inf = 0x3f3f3f3f;using namespace std;int n, m;
int dis[MAXN], u[MAXN], v[MAXN], w[MAXN];void bellford(int start)
{
for (int i = 1; i <= n; i++)dis[i] = inf;dis[start] = 0;for (int k = 1; k <= n - 1; k++)//外部循环n-1次{
int flag = 0;for (int i = 1; i <= m; i++)//按边松弛{
if (dis[u[i]] < inf && dis[v[i]] > dis[u[i]] + w[i]){
dis[v[i]] = dis[u[i]] + w[i];flag = 1;}}if (!flag) break;//本轮dis数组没有更新，直接退出结束算法。}
}int judge()
{
int flag = 0;for (int i = 1; i <= m; i++){
if (dis[v[i]] > dis[u[i]] + w[i])flag = 1;break;}if (flag){
printf("此图含有负权回路\n");return 0;}elsereturn 1;
}void print()
{
for (int i = 1; i <= n; i++)printf("%d ", dis[i]);//输出每个点到单源起点的最短距离printf("\n");
}
int main()
{
while (scanf_s("%d%d", &n, &m) != EOF && (n || m)){
//读入边for (int i = 1; i <= m; i++)scanf_s("%d%d%d", &u[i], &v[i], &w[i]);int start;//读入起点scanf_s("%d", &start);bellford(start);if (judge())print();}return 0;
}