题目链接:
https://cn.vjudge.net/problem/18676/origin
Problem Description
Unlike single maze, double maze requires a common sequence of commands to solve both mazes. See the figure below for a quick understanding.
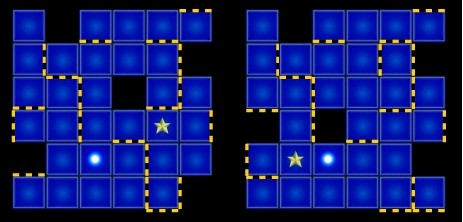
A maze is made up of 6*6 cells. A cell can be either a hole or a square. Moreover, a cell may be surrounded by barriers. There is ONLY one start cell (with a ball) and ONLY one end cell (with a star) in a single maze.These two cells are both squares. It is possible that the start cell and the end cell are the same one. The goal of a single maze is to move the ball from the start cell to the end cell. There are four commands in total,'L', 'D', 'R' and 'U' corresponding to moving the ball left, down, right and up one cell, respectively. The barriers may make the commands take no effect, i.e., the ball does NOT move if there is a barrier on the way.
When the ball gets to a hole or outside of the maze, it fails. A double maze is made up of two single mazes. The commands control two balls simultaneously, and the movements of two balls are according to the rules described above independently. Both balls will continue to move simultaneously if at least one of the balls has not got to the end cell.
So, a ball may move out of the end cell since the other ball has not been to the target. A double maze passes when both balls get to their end cells, or fails if either of the two mazes fails. The goal of double maze is to get the shortest sequence of commands to pass. If there are multiple solutions, get the lexical minimum one.
To simplify the input, a cell is encoded to an integer as follows. The lowest 4 bits signal the existence of the barriers around a cell. The fifth bit indicates whether a cell is a hole or not. The sixth and seventh bits are set for the start cell and end cell. Details are listed in the following table with bits counted from lowest bit. For a barrier, both of the two adjacent cells will have the corresponding barrier bit set. Note that the first two mazes in the sample input is the encoding of two mazes in the figure above, make sure you understand the encoding right.


A maze is made up of 6*6 cells. A cell can be either a hole or a square. Moreover, a cell may be surrounded by barriers. There is ONLY one start cell (with a ball) and ONLY one end cell (with a star) in a single maze.These two cells are both squares. It is possible that the start cell and the end cell are the same one. The goal of a single maze is to move the ball from the start cell to the end cell. There are four commands in total,'L', 'D', 'R' and 'U' corresponding to moving the ball left, down, right and up one cell, respectively. The barriers may make the commands take no effect, i.e., the ball does NOT move if there is a barrier on the way.
When the ball gets to a hole or outside of the maze, it fails. A double maze is made up of two single mazes. The commands control two balls simultaneously, and the movements of two balls are according to the rules described above independently. Both balls will continue to move simultaneously if at least one of the balls has not got to the end cell.
So, a ball may move out of the end cell since the other ball has not been to the target. A double maze passes when both balls get to their end cells, or fails if either of the two mazes fails. The goal of double maze is to get the shortest sequence of commands to pass. If there are multiple solutions, get the lexical minimum one.
To simplify the input, a cell is encoded to an integer as follows. The lowest 4 bits signal the existence of the barriers around a cell. The fifth bit indicates whether a cell is a hole or not. The sixth and seventh bits are set for the start cell and end cell. Details are listed in the following table with bits counted from lowest bit. For a barrier, both of the two adjacent cells will have the corresponding barrier bit set. Note that the first two mazes in the sample input is the encoding of two mazes in the figure above, make sure you understand the encoding right.

Input
The first line of input gives the total number of mazes, T (1 < T ≤ 20). Then follow T mazes. Each maze is a 6*6 matrix, representing the encoding of the original maze. There is a blank line between mazes.
Output
For every two consecutive mazes, you should treat them as a double maze and output the answer. So there are actually T - 1 answers. For each double maze, output the shortest sequence of commands to pass. If there are multiple solutions, output the lexicographically minimum one. If there is no way to pass, output -1 instead.
Sample Input
3 16 0 18 16 18 24 20 19 24 16 28 1 18 28 17 0 22 17 25 20 17 18 88 20 2 16 48 28 17 16 24 16 16 20 23 116 0 18 16 18 24 20 19 24 20 29 1 18 28 17 16 22 17 8 20 1 18 24 20 19 80 48 24 16 0 24 16 16 16 22 1918 16 18 16 18 80 24 18 24 16 24 18 18 24 0 0 18 24 24 18 0 0 24 18 18 24 18 16 18 24 56 18 24 18 24 18
Sample Output
RRLULLLRRDLU RURDRLLLURDULURRRRRDDU
题目大意:
对于每两个矩阵,同时移动球,使得两个球从各自的起点到各自的终点。起始点和终点以及栅栏和黑洞的给出方式是那个数的二进制对应的位置所描述的,题目的表中有描述。
思路:
BFS即可。自己写的时候写了很久,需要注意可能因为栅栏在,而往某个方向移动移不出6*6方格外的情况,这时候判断不能以原有的方式判断是否移出去,一定要注意。
具体实现中,有栅栏就在原地呆着不动就行。
应该学习的代码:
#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;
const int N = 6;
int n, t;
char s[5] = {"DLRU"};
int f[N][N][N][N];
int nxt[4][2] = {
{1,0},{0,-1},{0,1},{-1,0}};
struct maze
{int a[N][N];int bx, by, ex, ey;int d[N][N][4];void read(){for(int i = 0; i <= 5; i++)for(int j = 0; j <= 5; j++){scanf("%d", &a[i][j]);for(int k = 0; k <= 1; k++) d[i][j][k^1] = a[i][j] & (1<<k);for(int k = 2; k <= 3; k++) d[i][j][k] = a[i][j] & (1<<k);if(a[i][j]&(1<<5)) bx = i, by = j;if(a[i][j]&(1<<6)) ex = i, ey = j;a[i][j] = a[i][j] & (1<<4);}}bool check(int x, int y){return x == ex && y == ey;}bool Move(int t, int x, int y, int &xx, int &yy){if(d[x][y][t]) {xx = x; yy = y; return true;}int nx = x + nxt[t][0], ny = y + nxt[t][1];if(nx < 0 || nx > 5 || ny < 0 || ny > 5 || !a[nx][ny]) return false;xx = nx;yy = ny; return true;}
}mp[2];
struct point
{int x1, y1, x2, y2;point(int x1 = 0, int y1 = 0, int x2 = 0, int y2 = 0):x1(x1), y1(y1), x2(x2), y2(y2){};
}pre[N][N][N][N];
void output(int x1, int y1, int x2, int y2)
{if(f[x1][y1][x2][y2] == -2)return ;point p = pre[x1][y1][x2][y2];output(p.x1, p.y1, p.x2, p.y2);printf("%c", s[f[x1][y1][x2][y2]]);
}
bool bfs(maze &a, maze &b)
{queue<point> q;q.push(point(a.bx, a.by, b.bx, b.by));f[a.bx][a.by][b.bx][b.by] = -2;while(!q.empty()){point tem = q.front();q.pop();if(a.check(tem.x1, tem.y1) && b.check(tem.x2, tem.y2)){output(tem.x1, tem.y1, tem.x2, tem.y2);puts("");return true;}int x1, y1, x2, y2;for(int i = 0; i <= 3; i++){if(!a.Move(i, tem.x1, tem.y1, x1, y1)) continue;if(!b.Move(i, tem.x2, tem.y2, x2, y2)) continue;if(f[x1][y1][x2][y2] != -1) continue;f[x1][y1][x2][y2] = i;pre[x1][y1][x2][y2] = tem;q.push(point(x1, y1, x2, y2));}}return false;
}
int main()
{scanf("%d", &n);for(mp[t = 0].read(); --n; t ^= 1){memset(f, -1, sizeof(f));mp[t^1].read();if(!bfs(mp[t], mp[t^1]))printf("-1\n");}return 0;
}本弱的代码:
#include<bits/stdc++.h>
using namespace std;
struct Node
{bool dir[5];Node(){ memset(dir, false, sizeof(dir));}
}mat[2][8][8];
int nxt[4][2] = {1, 0, 0, -1, 0, 1, -1, 0};
int bx1, bx2, by1, by2, ex1, ex2, ey1, ey2;
string str[4] = {"D", "L", "R", "U"};
bool vis[6][6][6][6], flag;
void read(int t)
{int tem;for(int i = 0; i <= 5; i++)for(int j = 0; j <= 5; j++){scanf("%d", &tem);memset(mat[t][i][j].dir, false, sizeof(mat[t][i][j].dir));if(tem&(1<<1)) mat[t][i][j].dir[0] = true;if(tem&1) mat[t][i][j].dir[1] = true;if(tem&(1<<2)) mat[t][i][j].dir[2] = true;if(tem&(1<<3)) mat[t][i][j].dir[3] = true;if((tem&(1<<4)) == 0) mat[t][i][j].dir[4] = true;if(tem&(1<<5)) {bx2 = i; by2 = j;}if(tem&(1<<6)) {ex2 = i; ey2 = j;}}
}
struct Path
{int x1, y1, x2, y2;string s = "";Path(int _x1 = 0, int _y1 = 0, int _x2 = 0, int _y2 = 0):x1(_x1), y1(_y1), x2(_x2), y2(_y2){}
};
bool check(int t, int x, int y, int d)
{if(mat[t][x][y].dir[d])return true;return false;
}
bool judge(int x1, int y1, int x2, int y2)
{if(x1 == ex1 && y1 == ey1 && x2 == ex2 && y2 == ey2)return true;return false;
}
void solve(int t1, int t2)
{memset(vis, false, sizeof(vis));queue<Path> q;q.push(Path(bx1, by1, bx2, by2));vis[bx1][by1][bx2][by2] = true;bool is1, is2;while(!q.empty()){Path tem = q.front();q.pop();for(int i = 0; i <= 3; i++){is1 = is2 = false;int nx1 = tem.x1 + nxt[i][0];int ny1 = tem.y1 + nxt[i][1];int nx2 = tem.x2 + nxt[i][0];int ny2 = tem.y2 + nxt[i][1];if(check(t1, tem.x1, tem.y1, i)){nx1 = tem.x1;ny1 = tem.y1;is1 = true;}if(check(t2, tem.x2, tem.y2, i)){nx2 = tem.x2;ny2 = tem.y2;is2 = true;}if(nx1 < 0 || nx1 > 5 || ny1 < 0 || ny1 > 5 || nx2 < 0 || nx2 > 5 || ny2 < 0 || ny2 > 5)//特别要注意这个判断是在上面的判断之后continue;if(!is1 && mat[t1][nx1][ny1].dir[4])continue;if(!is2 && mat[t2][nx2][ny2].dir[4])continue;if(vis[nx1][ny1][nx2][ny2])continue;if(judge(nx1, ny1, nx2, ny2)){flag = true;cout << tem.s+str[i] << endl;return ;}vis[nx1][ny1][nx2][ny2] = true;Path aft;aft.x1 = nx1;aft.y1 = ny1;aft.x2 = nx2;aft.y2 = ny2;aft.s = tem.s + str[i];q.push(aft);}}
}
int main()
{int n, t = 0;scanf("%d", &n);for(int i = 1; i <= n; i++){bx1 = bx2;by1 = by2;ex1 = ex2;ey1 = ey2;read(t);if(i == 1){t = t^1;continue;}flag = false;if(bx1 == ex1 && by1 == ey1 && bx2 == ex2 && by2 == ey2){t = t^1;cout << endl;continue;}solve(t^1, t);t = t^1;if(!flag) puts("-1");}return 0;
}