题目链接
链接:https://ac.nowcoder.com/acm/contest/283/F
来源:牛客网
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 32768K,其他语言65536K
64bit IO Format: %lld
题目描述
众所周知,在各种对抗类游戏里装备都是很重要的一环,不同的出装方案会给玩家带来不同的强度。
dalao手里有N件装备,现在dalao要把装备分给N个队友,每个队友只能分一件装备,而每个队友穿上不同的装备会有不同程度的强度提升。
现在给出每个队友对每件装备的强度提升的值,请问dalao的所有分配方案里,最多能让团队的总强度提升多少呢?
输入描述:
第一行有一个整数T,表示数据的组数(不会超过150组)
每组数据第一行包含一个整数N,接下来会有N行,每行有N个整数,其中第 a 行的第 b 个数字表示第 a 个队友穿上第 b 件装备的强度提升。任何队员穿任何装备的强度提升都不会超过20000。
输出描述:
对于每组数据在一行内输出一个整数表示强度能够提升的最大值
示例1
输入
2
4
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
3
1 3 5
2 4 6
7 9 11输出
34
16思路:
本来感觉像是dp,可是不太好想,经zxz大佬提醒,发现是二分图匹配,于是就就试着用网络流做了一下。
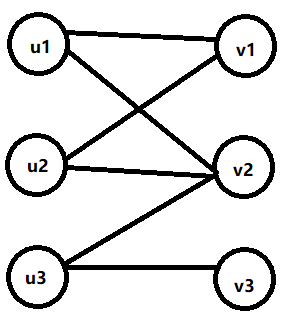
网络流解二分匹配,我们一般遇到的二分图是图一这样的,用网络流来解就是在两边加上源点和汇点,让这两个点分别和二分图的两部分连接(如图二),并且连接处的流量设置为1,花费设为0,在二分图加边时边的权值取负,流量设为1,这样从起点到终点的,最小费用最大流,就是二分图的最优匹配。

ac代码:
#include<stdio.h>
#include<string.h>
#include<queue>
#include<set>
#include<iostream>
#include<map>
#include<stack>
#include<cmath>
#include<algorithm>
#define ll long long
#define mod 1000000007
#define eps 1e-8
using namespace std;
const int MAXN = 10000;
const int MAXM = 100000;
const int INF = 0x3f3f3f3f;
struct Edge {int to,next,cap,flow,cost;
} edge[MAXM];
int head[MAXN],tol;
int pre[MAXN],dis[MAXN];
bool vis[MAXN];
int N;//节点总个数,节点编号从 0 ~ N-1
void init(int n) {N = n;tol = 0;memset(head,-1,sizeof(head));
}
void addedge(int u,int v,int cap,int cost) {edge[tol].to = v;edge[tol].cap = cap;edge[tol].cost = cost;edge[tol].flow = 0;edge[tol].next = head[u];head[u] = tol++;edge[tol].to = u;edge[tol].cap = 0;edge[tol].cost = -cost;edge[tol].flow = 0;edge[tol].next = head[v];head[v] = tol++;
}
bool spfa(int s,int t) {queue<int>q;for(int i = 0; i < N+1; i++) {dis[i] = INF;vis[i] = false;pre[i] = -1;}dis[s] = 0;vis[s] = true;q.push(s);while(!q.empty()) {int u = q.front();q.pop();vis[u] = false;for(int i = head[u]; i != -1; i = edge[i].next) {int v = edge[i].to;if(edge[i].cap > edge[i].flow && dis[v] > dis[u] + edge[i].cost ) {dis[v] = dis[u] + edge[i].cost;pre[v] = i;if(!vis[v]) {vis[v] = true;q.push(v);}}}}if(pre[t] == -1)return false;else return true;
}
//返回的是最大流,cost 存的是最小费用
int minCostMaxflow(int s,int t,int &cost) {int flow = 0;cost = 0;while(spfa(s,t)) {int Min = INF;for(int i = pre[t]; i != -1; i = pre[edge[i^1].to]) {if(Min > edge[i].cap - edge[i].flow)Min = edge[i].cap - edge[i].flow;}for(int i = pre[t]; i != -1; i = pre[edge[i^1].to]) {edge[i].flow += Min;edge[i^1].flow -= Min;cost += edge[i].cost * Min;}flow += Min;}return flow;
}
int rb[5005];
int main()
{int n,m,t;scanf("%d",&t);while(t--){scanf("%d",&n);m=n;for(int i=0;i<=m+2;i++){rb[i]=i+n;}init(n+m+2);int u,v,w;for(int i=1;i<=n;i++)addedge(0,i,1,0);for(int i=1;i<=m;i++)addedge(rb[i],n+m+1,1,0);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){scanf("%d",&w);addedge(i,rb[j],1,-w);}}int c;minCostMaxflow(0,n+m+1,c);cout<<-c<<endl;}return 0;
}