题目
D. Permutation Transformation
排列是一个长度为n的序列,从1到n,其中所有的数字只出现一次。例如,[1],[3、5、2、1,4],[1、3、2]排列,和[2、3、2],[4、3、1][0]。Polycarp最近被赋予了一个长度n的排列a[1 n]。Polycarp更喜欢树而不是排列,所以他想把排列a转换成一个有根的二叉树。他将一个由不同整数组成的数组转换成一棵树,如下所示:数组的最大元素成为树的根;最大值左边的所有元素构成一个左子树(根据相同的规则构建,但应用于数组的左边部分),但如果最大值左边没有元素,那么根就没有左子树;最大值右边的所有元素构成一个右子树(根据相同的规则构建,但应用到数组的右边),但是如果最大值右边没有元素,那么根就没有右子树。例如,如果他建造树通过排列a =(3、5、2、1,4],然后根将元素a2 = 5 ,和左子树的树,将建子阵列[1]=[3],和正确的子数组一个[3 - 5]=[2、1,4]。因此,将构建以下树
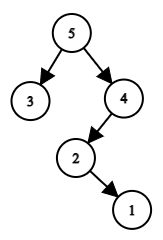
排列a=[3,5,2,1,4]对应的树。另一个例子:设排列为a=a=[1,3,2,7,5,6,4]。在这种情况下,树是这样的
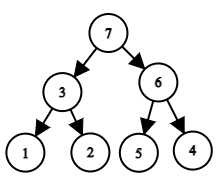
排列a=[1,3,2,7,5,6,4]对应的树a=[1,3,2,7,5,6,4]。
让我们用dv表示顶点av的深度,也就是说,从根到编号为av的顶点的路径上的边数。注意,根深度为零。给定排列a,对于每个顶点,求dv的值。
输入
第一行包含一个整数t(1≤t≤100)—测试用例的数量。然后是t测试用例。
每个测试用例的第一行包含一个整数n(1≤n≤100)——排列的长度。
后面跟着n数a1,a2,…,an
输出
对于每个测试用例,输出n值- d1,d2,…,dn
题意
给定n元素数组a,将数组a转化为一棵二叉树,规则如下:
1.a中最大值作二叉树之根
2.最大值左侧的子数组构成左子树
3.最大值右侧的子数组构成右子树
4.子树的构成规则也如上
任务是顺序输出数组中每个数在树中的深度
Example
input
Copy
3 5 3 5 2 1 4 1 1 4 4 3 1 2
output
Copy
1 0 2 3 1 0 0 1 3 2
/*递归简介
递归算法的 基本思想 是:把规模大的、较难解决的问题变成规模较小的、易解决的同一问题。规模较小的问题又变成规模更小的问题,并且小到一定程度可以直接得出它的解,从而得到原来问题的解。
(递归来源于数学中的归纳法)递归的三个条件
1. 解决问题时,可以把一个问题转化为一个新的问题,而这个新的问题的解决方法仍与原问题的解法相同,只是所处理的对象有所不同,这些被处理的对象之间是有规律的递增或递减;
2. 可以通过转化过程是问题得到解决;
3. 必定要有一个明确的结束递归的条件,否则递归将会无止境地进行下去,直到耗尽系统资源。也就是说必须要某个终止递归的条件。如求阶乘问题,我们要求n的阶乘(n!),可以把这个问题转化为n(n-1)!,而要求(n-1)!又可转化为(n-1)(n-2)!,……,这里面都有一个一个数乘以另一个数阶乘的问题,被处理的对象分别是n,n-1,……,是有规律的递减。但是我们不能让程序无休止的乘下去,必须要给他一个结束条件,该问题恰好有一个结束条件,那就是当n=0时,0!=1。*/
代码
#include <iostream>
#include <cstring>
using namespace std;
void qiuda(int left,int right,int depth);//求当前数组中最大的数
int n,i,a[110],shendu[110]={0},t;
int main()
{cin >>t;while(t--){cin >> n;for(i=0;i<n;i++)cin >> a[i];qiuda(0,n-1,0);for(i=0;i<n;i++) //输出a[i]在shendu[i]对应的深度cout <<shendu[i]<<' ';cout <<endl;}return 0;
}
void qiuda(int left,int right,int depth)
{int i;if(left>right)return;int maxident=left; //当前最大数的下标for(i=left;i<=right;i++){if(a[i]>a[maxident])maxident=i; //得到最大数的下标}shendu[maxident]=depth; //将深度赋给对应下标qiuda(left,maxident-1,depth+1); //求左边最大qiuda(maxident+1,right,depth+1); //求右边最大
}