题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5794
第六场多校唯一"做"出来的一题(小编觉得,像 A Boring Question(01)和 A Simple Nim(03)这种打个表莫名其妙就A的题没啥好讲的)。
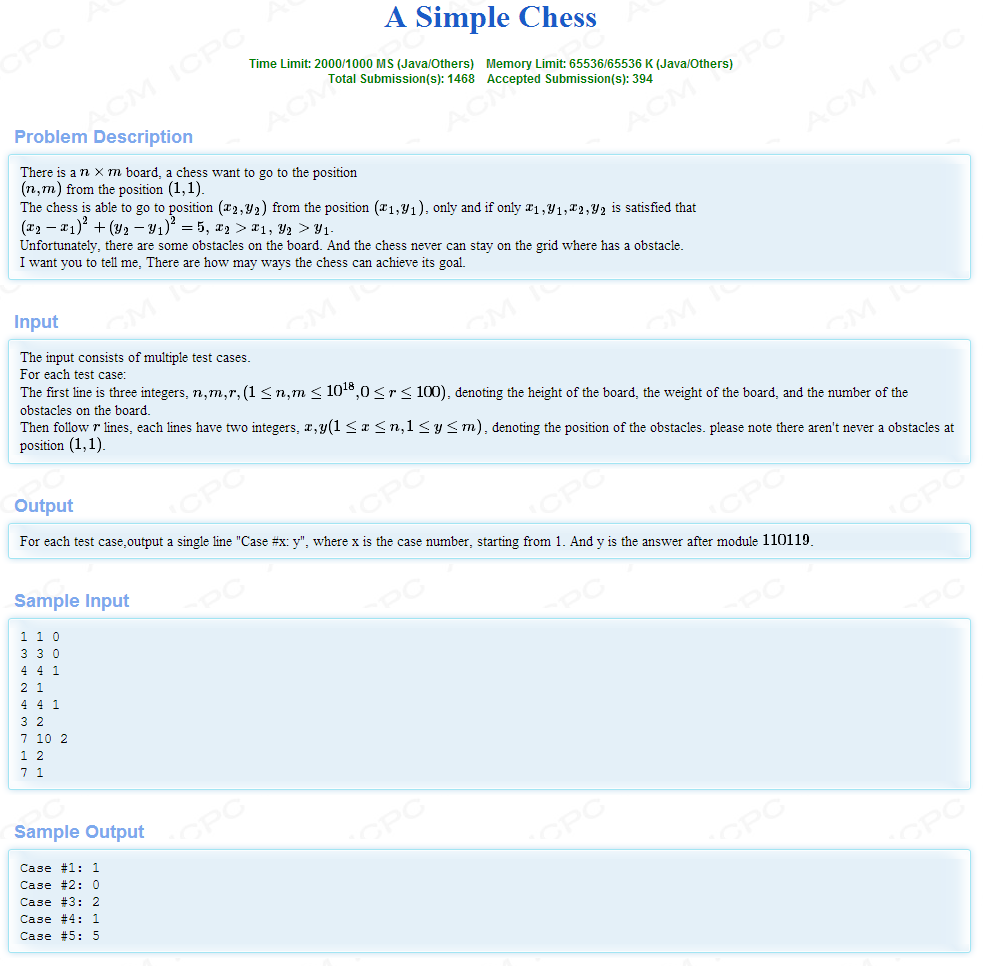
题意:给我们一个棋盘,棋盘上有r个障碍,我们能够从(1,1)出发,每一次能够向右下走日字,问我们走到终点的方案数。
很简单的一个容斥原理的运用,举个例子,我们从点i出发,途中有一个障碍点j,从点i到终点的方案数,就等于总方案数减去从j到终点的方案数*从点i到点j的方案数。
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long LL;
const LL mod=110119;
const LL maxn=100;
LL dp[maxn*10+20];
LL f[mod*10];
struct Point{LL x,y;}p[maxn+20];
bool cmp(Point a,Point b)
{if(a.x<b.x)return 1;if(a.x>b.x)return 0;return a.y<b.y;
}
LL Power_mod(LL a, LL b, LL p)
{LL res = 1;while(b){if(b&1) res = (res * a) % p;a = (a*a) % p;b >>= 1;}return res;
}
LL Comb(LL a, LL b, LL p)
{if(a < b) return 0;if(a == b) return 1;LL ans=f[a]*Power_mod(f[b]*f[a-b]%p,p-2,p)%p;return ans;
}
LL Lucas(LL n, LL m, LL p)
{LL ans = 1;while(n && m && ans){ans = (ans*Comb(n%p, m%p, p)) % p;n /= p;m /= p;}return ans;
}
LL get(LL x,LL y)
{if((x+y)%3 || max(x,y)>2*min(x,y))return 0;LL a=(x+y)/3,b=(2*x-y)/3;if(a<0 || b<0)return 0;return Lucas(a,b,mod);
}
int main()
{ LL i,j,k,h,w,n,cas=0;f[0]=f[1]=1;for(i=2;i<=mod+20;i++)f[i]=f[i-1]*i%mod; while(~scanf("%I64d%I64d%I64d",&h,&w,&n)){for(i=0; i<n; i++) scanf("%I64d%I64d",&p[i].x,&p[i].y);if((h+w-2)%3 || max(h-1,w-1)>2*min(h-1,w-1)){printf("Case #%I64d: 0\n",++cas);continue;}sort(p,p+n,cmp),p[n].x=h,p[n].y=w;for(i=0; i<=n; i++){dp[i] = get(p[i].x-1,p[i].y-1);for(j=0; j<i; j++)if(p[j].x <= p[i].x && p[j].y <= p[i].y){dp[i] -= get(p[i].x-p[j].x,p[i].y-p[j].y)*dp[j];dp[i] = (dp[i]%mod+mod)%mod; } }printf("Case #%I64d: %I64d\n",++cas,dp[n]);}return 0;
}