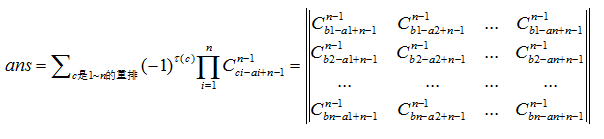参考博客:HDU 5852 Intersection is not allowed!(组合数学+行列式)
下面是该博客的解释:
首先考虑两个棋子的情况,即一个棋子从a1到b1,另一个棋子从a2到b2,两条路径不交叉的方案数,首先不考虑交叉方案数显然是C(b1-a1+n-1,n-1)*C(b2-a2+n-1,n-1),对于一个a1->b1,a2->b2且路径交叉的方案,如果我们把最下面一个交叉点之后的两条路径交换那么就对应了一个a1->b2,a2->b1的方案;对于一个a1->b2,a2->b1的方案,显然这两条路径必然会相交,那么我们把最后一个交叉点之后的两条路径交换就又对应一个a1->b1,a2->b2的路径交叉的方案,故我们建立了a1->b1,a2->b2交叉路径与a1->b2,a2->b1的方案的一一对应,那么不合法方案数就是C(b2-a1+n-1,n-1)*C(b1-a2+n-1,n-1)
对于多个棋子的情况,由容斥原理,假设某些棋子路径发生了交叉,那么我们采用两个棋子的分析方法,把这些交叉的路径从最后下面一个交叉点之后交换,那么就变成了一个1~n序列的重排,我们不妨设其为c序列,表示第i个棋子从(1,ai)出发到(n,ci),那么这个排列对答案的贡献就取决于c序列的逆序对数,逆序对数为奇则做负贡献,为偶则做正贡献,那么就有
故问题转化为求一个n阶方阵行列式,用高斯消元O(n^3)即可解决
第一次写高斯消元,记录一下,还挺简单的,是高斯消元简单(⊙o⊙)(不是这个题目简单)
像我这种弱鸡,也只能看看大佬们的题解来维持生活这样子。
我的代码:
#include<cstdio>
#include<algorithm>
using namespace std;typedef long long ll;
const ll mod=(ll)1000000007;
const int maxn=110;
const int maxm=100010;ll ans[maxn][maxn];
ll f[maxm*2],inv[maxm];
int A[maxn],B[maxn];
int n,k;inline ll mypow(ll a,ll b){
ll sum=1;while(b){
if(b&1) sum=sum*a%mod;a=a*a%mod;b>>=1;}return sum;
}void init(){
f[0]=1;for(int i=1;i<maxm*2;i++) f[i]=f[i-1]*i%mod;inv[maxm-1]=mypow(f[maxm-1],mod-2);for(int i=maxm-2;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mod;
}inline ll C(int a,int b){
if(a<b) return 0;return f[a]*inv[b]%mod*inv[a-b]%mod;
}ll gauss(){
ll kaven=1;ll tmp=1;for(int i=1;i<=k;i++){
int ind=-1;for(int j=i;j<=k;j++){
if(ans[j][i]){
ind=j;break;}}if(ind==-1) return 0;if(ind!=i){
tmp*=-1;for(int j=i;j<=k;j++) swap(ans[ind][j],ans[i][j]);}ll tmp_inv=mypow(ans[i][i],mod-2);for(int j=i+1;j<=k;j++){
if(ans[j][i]){
kaven=kaven*tmp_inv%mod;for(int t=i+1;t<=k;t++) ans[j][t]=(ans[j][t]*ans[i][i]%mod-ans[i][t]*ans[j][i]%mod+mod)%mod;ans[j][i]=0;}}}for(int i=1;i<=k;i++) kaven=kaven*ans[i][i]%mod;return kaven;
}int main(){
init();int T;scanf("%d",&T);while(T--){
scanf("%d%d",&n,&k);for(int i=1;i<=k;i++) scanf("%d",&A[i]);for(int i=1;i<=k;i++) scanf("%d",&B[i]);for(int i=1;i<=k;i++){
for(int j=1;j<=k;j++){
ans[i][j]=C(n-1+B[j]-A[i],n-1); //也可ans[i][j]=C(n-1+B[i]-A[j],n-1),因为互为转置,结果是一样的,但经过测试前面那个好像更快一些}}ll kaven=gauss();printf("%lld\n",kaven);}
}