B - 滑动解锁

滑动解锁是智能手机一项常用的功能。你需要在3x3的点阵上，从任意一个点开始，反复移动到一个尚未经过的”相邻”的点。这些划过的点所组成的有向折线，如果与预设的折线在图案、方向上都一致，那么手机将解锁。两个点相邻当且仅当以这两个点为端点的线段上不存在尚未经过的点。此外，这条折线还需要至少经过4个点。

为了描述方便，我们给这9个点从上到下、从左到右依次编号1-9。那么1->2->3是不合法的，因为长度不足。1->3->2->4也是合不法的，因为1->3穿过了尚未经过的点2。2->4->1->3->6是合法的，因为1->3时点2已经被划过了。

作为一个爱逛知乎的好少年，小Hi已经知道一共有389112种不同的解锁方案。不过小Hi不满足于此，他希望知道，当已经瞥视到一部分折线的情况下，有多少种不同的方案。

遗憾的是，小Hi看到的部分折线既不一定是连续的，也不知道方向。例如看到1-2-3和4-5-6，那么1->2->3->4->5->6，1->2->3->6->5->4, 3->2->1->6->5->4->8->9等都是合法的方案。

Input

第一行包含一个整数T(1 <= T <= 10)，代表测试数据组数。

每个测试数据第一行是一个整数N(0 <= N <= 8)，代表小Hi看到的折线段数目。

以下N行每行包含两个整数X, Y (1 <= X, Y <= 9)，代表小Hi看到点X和点Y是直接相连的。

Output

对于每组数据输出合法的方案数目。

Sample Input

Sample Output

389112  
2  
258

【解析】

以题目描述，我们可以得到下图：
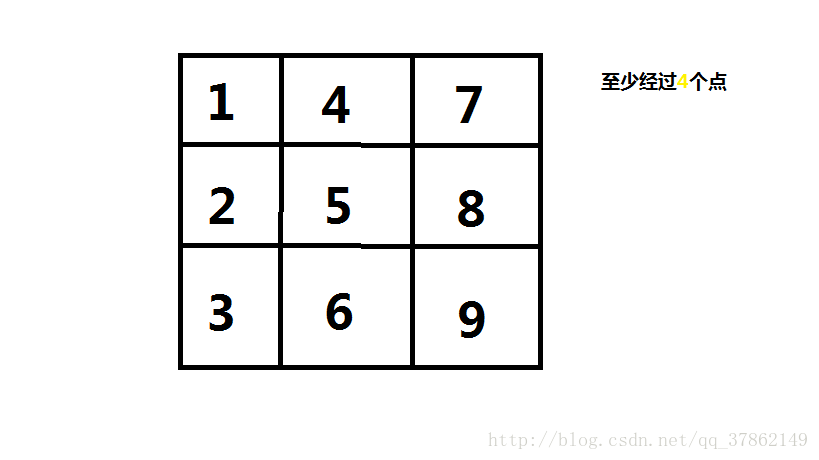
这里写图片描述
显然，这是一道深搜的题目。那么我们应该如何判断？以及如何深搜呢？题目首先告诉了我们有哪两个点是直接相连的。那么，我们为了方便判断后面深搜线段的合理性，首先，我们要对每个点进行初始化，找到每两个点之间所间隔的点，进行记录。然后进行的就是深搜，枚举点（即线段），后再进行判断它是否合理就行。剪枝：一条边的两个端点都被使用，但是这条边应该使用却没使用，则剪枝。

【AC代码】

#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn = 10 + 5;
int vis[maxn], ans, n, G[maxn][maxn], e[maxn][maxn];struct edge{int x, y;
}a[maxn];void init() {
   //初始化 memset(G, 0, sizeof(G));for(int i = 1; i <= 7; i+=3) G[i][i+2] = G[i+2][i] = i+1;for(int i = 1; i <= 3; ++i) G[i][i+6] = G[i+6][i] = i+3;G[1][9] = G[9][1] = G[3][7] = G[7][3] = 5;
}void dfs(int u, int cnt) {//is it possiblefor(int i = 0; i < n; ++i) {int x = a[i].x, y = a[i].y;if(vis[x] && vis[y] && !e[x][y] && !e[y][x]) return; //一条边的两个端点都被使用，但是这条边没使用则剪枝 }int flag = 1;for(int i = 0; i < n; ++i) {if(!e[a[i].x][a[i].y] && !e[a[i].y][a[i].x]) {flag = 0;break;}}if(flag && cnt >= 4) ans++;for(int i = 1; i <= 9; ++i) {if(u != i && !vis[i] && vis[G[u][i]]) {vis[i] = e[u][i] = 1;dfs(i, cnt+1);vis[i] = e[u][i] = 0;}}
}int main() {init();int t;scanf("%d",&t);while(t--){scanf("%d", &n);for(int i = 0; i < n; ++i) scanf("%d%d", &a[i].x, &a[i].y);ans = 0;for(int i = 1; i <= 9; ++i) {memset(vis, 0, sizeof(vis));memset(e, 0, sizeof(e));vis[0] = vis[i] = 1;dfs(i, 1);}printf("%d\n", ans);}return 0;
}