【读书笔记】Feature Scaling （特征缩放）：归一化、标准化、中心化

created on: 2020-01-20

@author: 假如我年华正好

Feature Scaling

WHY？

归一化/标准化实质是一种线性变换（对向量$X$按比例缩放，再进行平移），在样本给定的情况下，$X_{max}$，$X_{min}$，$\mu$，$\sigma$ 都可看作常数。

线性变换有很多良好的性质，决定了对数据改变后不会造成“失效”，反而能提高数据的表现，这些性质是归一化/标准化的前提。比如有一个很重要的性质：

• 线性变换不会改变原始数据的数值排序（不改变原始数据的分布状态）。

为什么要归一化/标准化？

1. 某些模型求解需要

   1. 如果输入范围不同，某些算法无法正常工作。例如逻辑回归，神经网络
   2. 梯度下降的收敛速度非常慢慢甚至完全无法完成有效训练。 归一化/标准化后可以加快梯度下降的求解速度，即提升模型的收敛速度。（梯度下降是Logistic回归、支持向量机、神经网络等常用的优化算法。）
   3. 一些分类器需要计算样本之间的距离（如欧氏距离），例如KNN。如果一个特征值域范围非常大，那么距离计算就主要取决于这个特征，从而与实际情况相悖（比如这时实际情况是值域范围小的特征更重要）

   【?注意】：基于树的算法几乎是唯一不受输入大小影响的算法

2. 为了做无量纲化
   使得不同度量之间的特征具有可比性；
   对目标函数的影响体现在几何分布(离散型概率分布)上，而不是数值上

3. 避免数值问题
   太大的数会引发数值问题。

需要归一化的机器学习算法

（参考来源：https://blog.csdn.net/pipisorry/article/details/52247379）

• 有些模型在各个维度进行不均匀伸缩后，最优解与原来不等价，例如SVM（距离分界面远的也拉近了，支持向量变多？）。对于这样的模型，除非本来各维数据的分布范围就比较接近，否则必须进行标准化，以免模型参数被分布范围较大或较小的数据dominate。

• 有些模型在各个维度进行不均匀伸缩后，最优解与原来等价，例如logistic regression（因为θ的大小本来就自学习出不同的feature的重要性吧？）。对于这样的模型，是否标准化理论上不会改变最优解。但是，由于实际求解往往使用迭代算法，如果目标函数的形状太“扁”，迭代算法可能收敛得很慢甚至不收敛（模型结果不精确）。所以对于具有伸缩不变性的模型，最好也进行数据标准化。

• 有些模型/优化方法的效果会强烈地依赖于特征是否归一化，如LogisticReg，SVM，NeuralNetwork，SGD等。

• 不需要归一化的模型：

  • 0/1取值的特征通常不需要归一化，归一化会破坏它的稀疏性。

  • 有些模型则不受归一化影响，如DecisionTree。

---

HOW？

归一化（normalization）

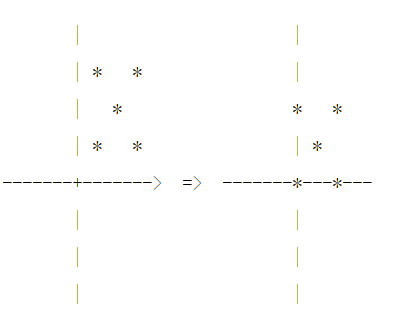
• 把数据映射到 [0,1]（或者 [-1, 1]）区间内

• 把有量纲表达式变成无量纲的纯量，便于不同单位或量级的指标能够进行比较和加权。

• 缩放仅仅跟最大、最小值的差别有关

• 区间放缩法是归一化的一种

• Min-Max Normalization（也叫离差标准化）：输出范围 [0, 1]

$$\frac{X_i?X_{min}}{X_{max}?X_{min}}$$

（[图片来源](https://blog.csdn.net/qq_36523839/article/details/82919412)）

from sklearn import preprocessing
norm_x = preprocessing.MinMaxScaler().fit_transform(x)

（[图片来源](https://www.meiwen.com.cn/subject/vgmveqtx.html)）

• 非线性归一化：

  • 经常用在数据分化比较大的场景，有些数值很大，有些很小。该方法包括log、指数、正切等
  • 需要根据数据分布的情况，决定非线性函数的曲线
  • 例如 对数函数转换：$y=\log (X)$

归一化后的好处

1. 提升模型的收敛速度

如左图所示，未归一化时形成的等高线偏椭圆，迭代时很有可能走“之”字型路线（垂直长轴），从而导致迭代很多次才能收敛。而如右图对两个特征进行了归一化，对应的等高线就会变圆，在梯度下降进行求解时能较快的收敛。（[图片来源](https://www.jianshu.com/p/95a8f035c86c)）

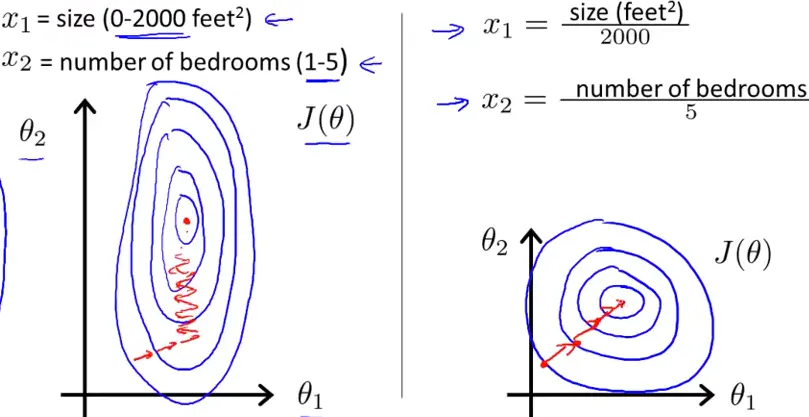
2. 提升模型的精度
   在涉及到一些距离计算的算法时效果显著，比如算法要计算欧氏距离，归一化可以让各个特征对结果做出的贡献相同。
   当各指标间的水平相差很大时，如果直接用原始指标值进行分析，就会突出数值较高的指标在综合分析中的作用，相对削弱数值水平较低指标的作用。

---

标准化（standardization）

• Z-score规范化（标准差标准化 / 零均值标准化）

• 通过求z-score的方法，转换为标准正态分布（均值为0，标准差为1）

• 和整体样本分布相关，每个样本点都能对标准化产生影响，通过均值（$\mu$）和标准差（$\sigma$）体现出来。

• 也能取消由于量纲不同引起的误差，使不同度量之间的特征具有可比性

• 输出范围：[-∞, +∞]

$$\frac{X_i?\mu }{\sigma }$$

（[图片来源](https://blog.csdn.net/qq_36523839/article/details/82919412)）

from sklearn import preprocessing
std_x = preprocessing.StandardScaler().fit_transform(x)

标准化的好处

数据标准化也就是统计数据的指数化。数据标准化处理主要包括数据同趋化处理和无量纲化处理两个方面。数据同趋化处理主要解决不同性质数据问题，对不同性质指标直接加总不能正确反映不同作用力的综合结果，须先考虑改变逆指标数据性质，使所有指标对测评方案的作用力同趋化，再加总才能得出正确结果。数据无量纲化处理主要解决数据的可比性。经过上述标准化处理，原始数据均转换为无量纲化指标测评值，即各指标值都处于同一个数量级别上，可以进行综合测评分析。（原文链接：https://blog.csdn.net/pipisorry/article/details/52247379）

---

中心化（Zero-centered 或 Mean-subtraction）

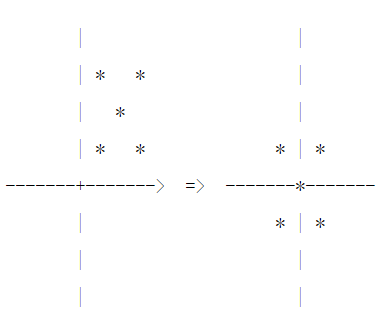
• 把数据整体移动到以0为中心点的位置
• 平均值为0，对标准差无要求
• 减去平均数，但没有除以标准差的操作（只有平移，没有缩放）

• PCA的时候需要做中心化（centering）（参考：CSDN博文）

• 与标准化的区别：（参考：CSDN博文）

  • 对数据进行中心化预处理，这样做的目的是要增加基向量的正交性。
  • 对数据标准化的目的是消除特征之间的差异性。便于对一心一意学习权重。
  

---

归一化和标准化的比较：

• 如果对输出结果范围有要求，用归一化
• 如果数据较为稳定，不存在极端的最大最小值，用归一化
• 如果数据存在异常值和较多噪音，用标准化，可以间接通过中心化避免异常值和极端值的影响
• 在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，标准化表现更好。

（参考来源：知乎回答）

• 归一化和标准化，都是将点平移然后缩短距离，但标准化不改变数据分布（几何距离）

  • 平移对于归一化以一个最小值为参照，标准化以均值为参照。
  • 缩放对于归一化以最大差值为参照，标准化以标准差为参照。
  • 标准化不改变几何距离是其公式定义的原因。
  • 需要根据实际的数据或场景需求来使用，以免适得其反，如：归一化后虽然平衡了权重，但也会或多或少破坏数据的结构。 （原文链接）
  

如果采用标准化，不改变样本在这两个维度上的分布，则左图还会保持二维分布的一个扁平性； 而采用归一化则会在不同维度上对数据进行不同的伸缩变化（归一区间，会改变数据的原始距离，分布，信息），使得其呈类圆形。虽然这样样本会失去原始的信息，但这防止了归一化前直接对原始数据进行梯度下降类似的优化算法时最终解被数值大的特征所主导。归一化后，各个特征对目标函数的影响权重是一致的。这样的好处是在提高迭代求解的精度。 （原文链接：https://blog.csdn.net/qq_36523839/article/details/82919412）

---

选择特征缩放方法的经验

?以下参考来源：GitHub项目：feature-engineering-and-feature-selection

Method	Definition	Pros	Cons
Normalization - Standardization (Z-score scaling)	removes the mean and scales the data to unit variance. z = (X - X.mean) / std	feature is rescaled to have a standard normal distribution that centered around 0 with SD of 1	compress the observations in the narrow range if the variable is skewed or has outliers, thus impair the predictive power.
Min-Max scaling	transforms features by scaling each feature to a given range. Default to [0,1]. X_scaled = (X - X.min / (X.max - X.min)	/	compress the observations in the narrow range if the variable is skewed or has outliers, thus impair the predictive power.
Robust scaling	removes the median and scales the data according to the quantile range (defaults to IQR) X_scaled = (X - X.median) / IQR	better at preserving the spread of the variable after transformation for skewed variables	/

from sklearn.preprocessing import RobustScaler
RobustScaler().fit_transform(X)

Z-score 和 Min-max方法将把大部分数据压缩到一个狭窄的范围，
而 robust scaler 在保持数据整体情况方面做得更好，尽管它不能从处理结果中移除异常值。
（但是请记住，清除/查找离群值是数据清理中的另一个主题，应该事先完成。）

1. 如果特性不是高斯型的，例如，skewed distribution 或有异常值，Normalization - Standardization 不是一个好的选择，因为它将把大多数数据压缩到一个狭窄的范围。
2. 但是，可以先转换成高斯型，再使用Normalization - Standardization。（这在3.4节 Feature Transformation中讨论。）
3. 在计算距离或协方差计算时(聚类、PCA和LDA等算法)，最好采用Normalization - Standardization，因为它将消除尺度对方差和协方差的影响。（ Explanation here）
4. Min-Max Scaling有着和 Normalization - Standardization 一样的缺点，而且新的数据可能不会被限制到[0, 1]，因为它们可能超出了原来的范围。一些算法，例如 深度神经网络更喜欢限制在0-1的输入，所以这是一个很好的选择。

?附加参考资源：

• A comparison of the three methods when facing skewed variables can be found here，6.3. Preprocessing data —— sklearn官方文档

---

---

附：对样本（而不是特征）进行Normalization

另外，在sklearn官方文档 中还有个Normalization（正则化），定义为：the process of scaling individual samples to have unit norm.

from sklearn import preprocessing
preprocessing.Normalizer(norm="l2").fit_transform(x)
# norm: The norm to use to normalize each non zero sample.
# ‘l1’, ‘l2’, or ‘max’, optional (‘l2’ by default)

• l1_norm 变换后每个样本的各维特征的绝对值和为１，，
• l2_norm 变换后每个样本的各维特征的平方和为１，，
• max_norm 变换将每个样本的各维特征除以该样本的最大值。

? 特别注意这里的 Normalizer 是对行（对样本）进行处理，而本文前面提到的都是对列（对特征）进行处理。

from sklearn import preprocessing
X = [[ 1., -1.,  2.],[ 2.,  0.,  0.],[ 0.,  1., -1.],[ 0.,  1., -1.]]
preprocessing.normalize(X, norm='l1', return_norm =True)

Out[1]: 
(array([[ 0.25, -0.25,  0.5 ],[ 1.  ,  0.  ,  0.  ],[ 0.  ,  0.5 , -0.5 ],[ 0.  ,  0.5 , -0.5 ]]), array([4., 2., 2., 2.]))

preprocessing.normalize(X, norm='l2', return_norm =True)

Out[2]: 
(array([[ 0.40824829, -0.40824829,  0.81649658],[ 1.        ,  0.        ,  0.        ],[ 0.        ,  0.70710678, -0.70710678],[ 0.        ,  0.70710678, -0.70710678]]),array([2.44948974, 2.        , 1.41421356, 1.41421356]))

preprocessing.normalize(X, norm='max', return_norm =True)

Out[3]: 
(array([[ 0.5, -0.5,  1. ],[ 1. ,  0. ,  0. ],[ 0. ,  1. , -1. ],[ 0. ,  1. , -1. ]]), array([2., 2., 1., 1.]))