文章目录
- 前言
- 一、路由算法引入
- 二、静态路由
- 三、动态路由
-
- 1.链路状态(LS)路由算法
- 2.距离向量(DV)路由算法
- 总结
前言
提示:以下是本篇文章正文内容
一、路由算法引入
路由器的功能:
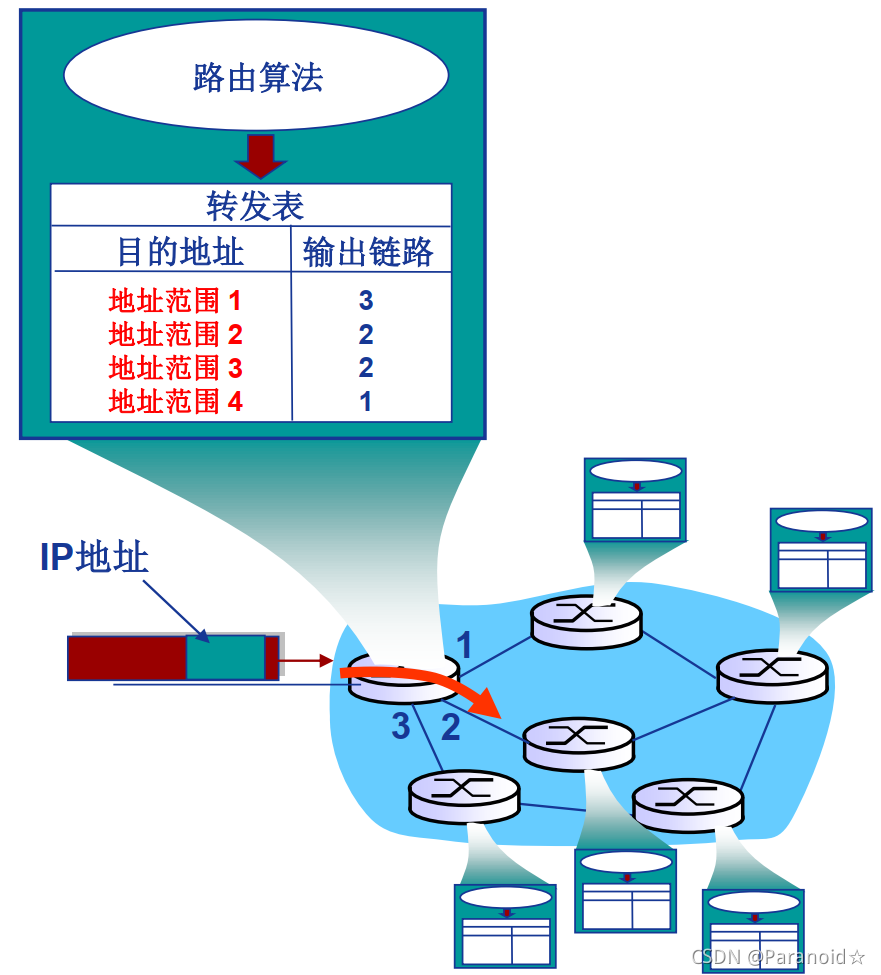
路由算法(协议)确定去往目的网络的最佳路径,转发表确定在本路由器如何转发分组
将实际中的路由器之间的关系抽象成图
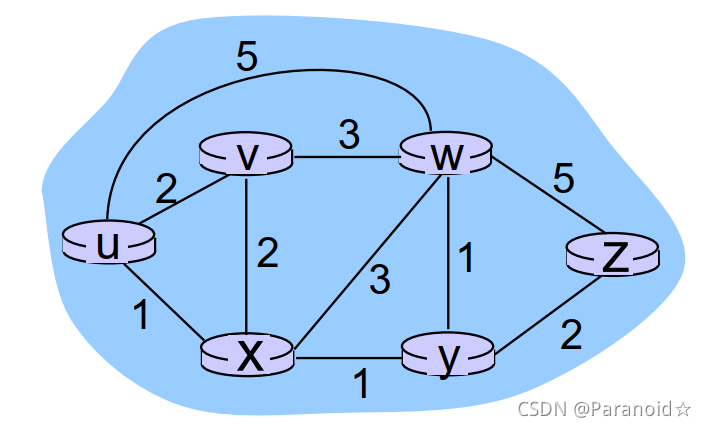
图: G = (N, E)
N = 路由器集合= { u, v, w, x, y, z }
E = 链路集合 ={ (u,v), (u,x), (v,x), (v,w), (x,w), (x,y), (w,y), (w,z), (y,z) }
费用(Costs):链路的费用,C(u,v) = 2
路由算法: 寻找源到目的最小费用路径的算法
路由器分组转发是通过路由表转发的,而路由表是通过各种算法得到的,从能否随网络的通信量或拓扑自适应地进行调整变化来划分,路由算法可分为两大类:静态路由与动态路由
二、静态路由
静态路由:需要手工配置,路由更新慢,优先级高,不适用于大型网络
三、动态路由
路由器间彼此交换信息,按照路由算法优化出路由表项
动态路由算法分为全局信息和分散信息
全局信息:所有路由器掌握完整的网络拓扑和链路费用信息,链路状态(LS)路由算法
分散(decentralized)信息:路由器只掌握物理相连的邻居以及链路费,邻居间信息交换、运算的迭代过程,距离向量(DV)路由算法
1.链路状态(LS)路由算法
Dijkstra 算法:所有结点(路由器)掌握网络拓扑和链路费用,通过“链路状态广播”使所有结点拥有相同信息,计算从一个结点(“源” )到达所有其他结点的最短路径获得该结点的转发表,k次迭代后,得到到达k个目的结点的最短路径
符号标记:
(1)c(x,y): 结点x到结点y链路费用;如果x和y不直接相连,则=∞
(2)D(v): 从源到目的v的当前路径费用值
(3)p(v): 沿从源到v的当前路径, v的前序结点
(4)N’: 已经找到最小费用路径的结点集合
算法描述:
1 初始化:
2 N’ = {u}
3 for 所有结点v
4 if v毗邻u
5 then D(v) = c(u,v)
6 else D(v) = ∞
7
8 Loop
9 找出不在 N’中的w ,满足D(w)最小
10 将w加入N’
11 更新w的所有不在N’中的邻居v的D(v) :
12 D(v) = min( D(v), D(w) + c(w,v) )
13 /*到达v的新费用或者是原先到达v的费用,或者是
14 已知的到达w的最短路径费用加上w到v的费用 */
15 until 所有结点在N’中 (loop 8)
示例一:
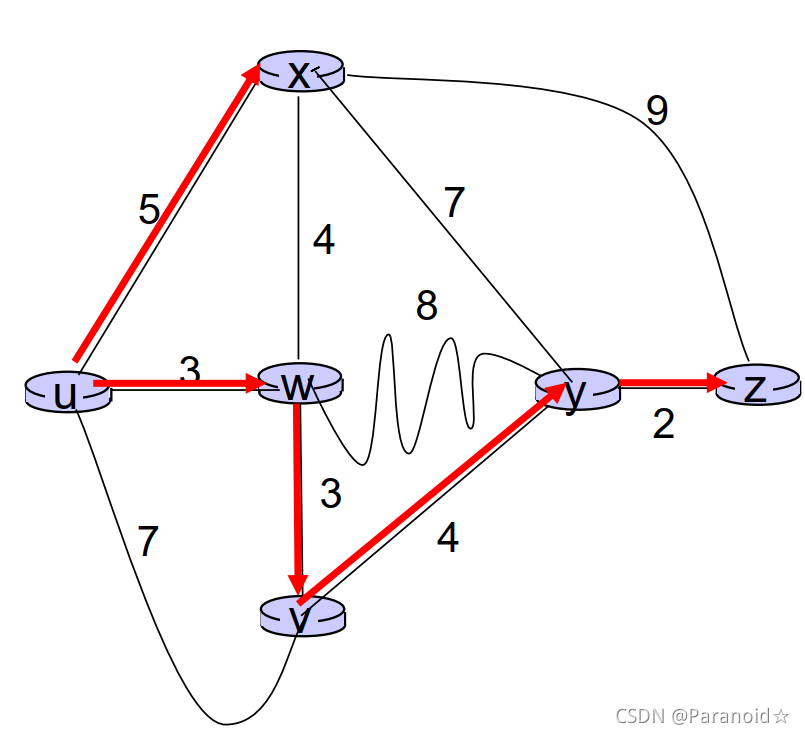
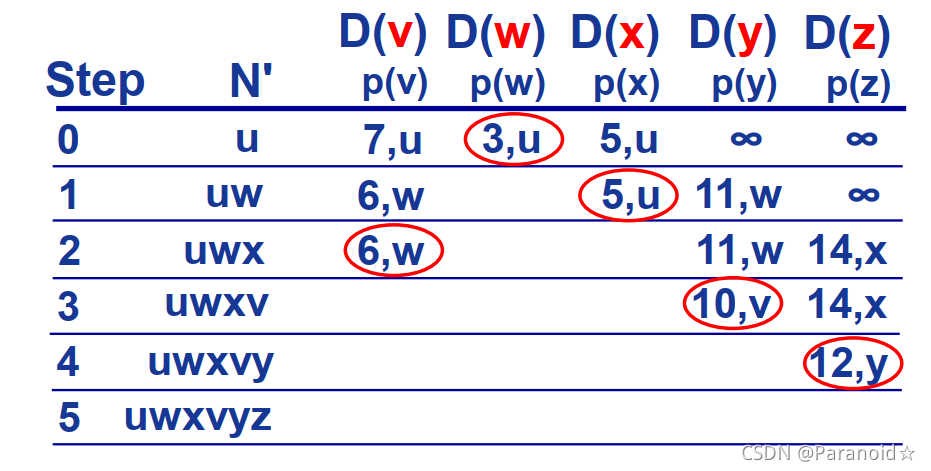
找出到目的地址的路径,求出最短路径即可
示例二:
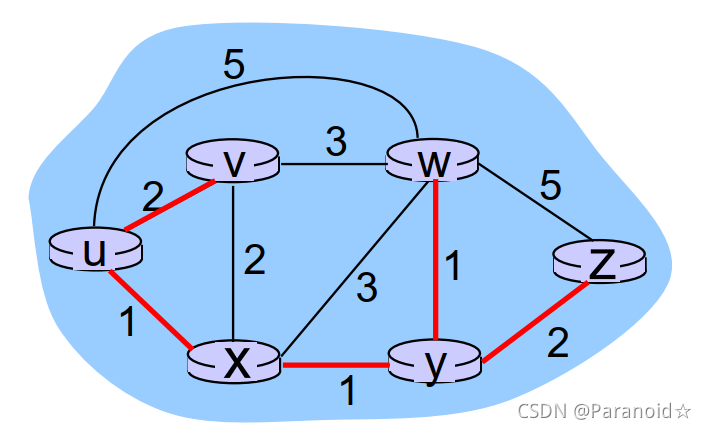
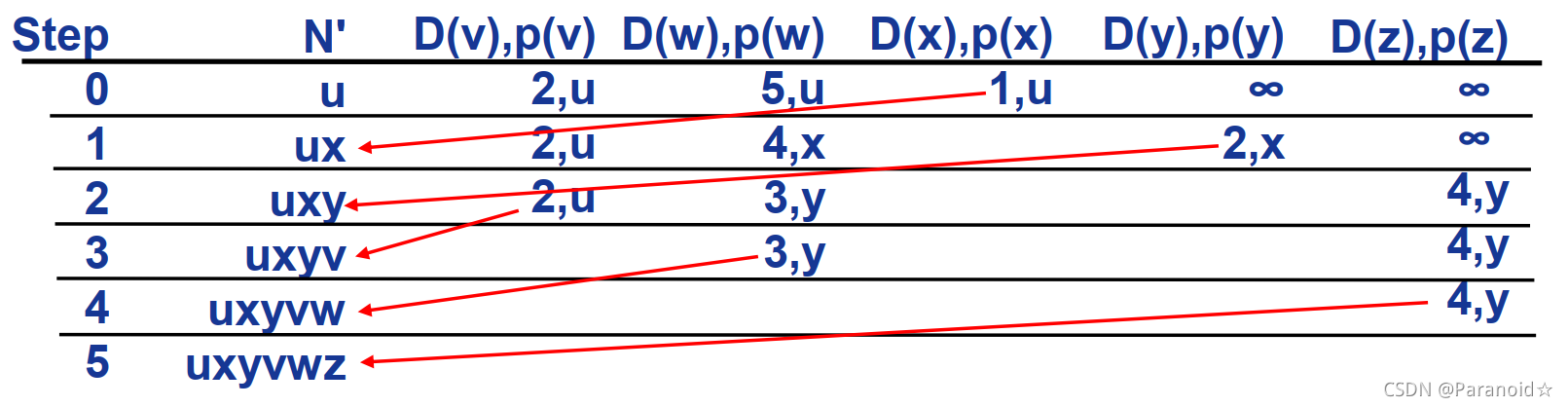
u的最终最短路径树:
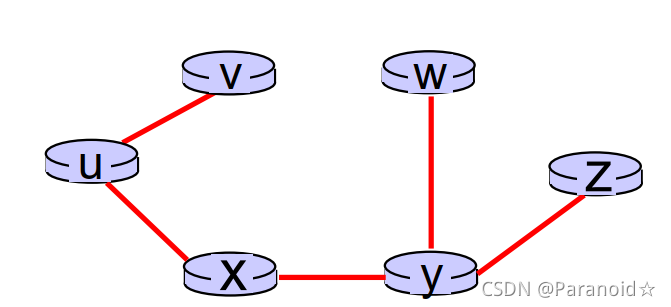
u的最终转发表:
| 目的 | 链路 |
|---|---|
| v | (u,v) |
| x | (u,x) |
| y | (u,x) |
| w | (u,x) |
| z | (u,x) |
算法分析:假设有n个结点
1.每次迭代: 需要检测所有不在集合N’中的结点w
2.n(n+1)/2次比较: O(n2)
3.更高效的实现: O(nlogn)
存在震荡(oscillations)可能
2.距离向量(DV)路由算法
Bellman-Ford方程(动态规划):
假设,dx(y):=从x到y最短路径的费用(距离)
则有:

核心思想:每个结点不定时地将其自身的DV估计发送给其邻居,当x接收到邻居的新的DV估计时, 即依据B-F更新其自身的距离向量估计:Dx(y) ← minv{c(x,v) + Dv(y)} for each node y ? N,Dx(y)将最终收敛于实际的最小费用 dx(y),结点获得最短路径的下一跳, 该信息用于转发表中
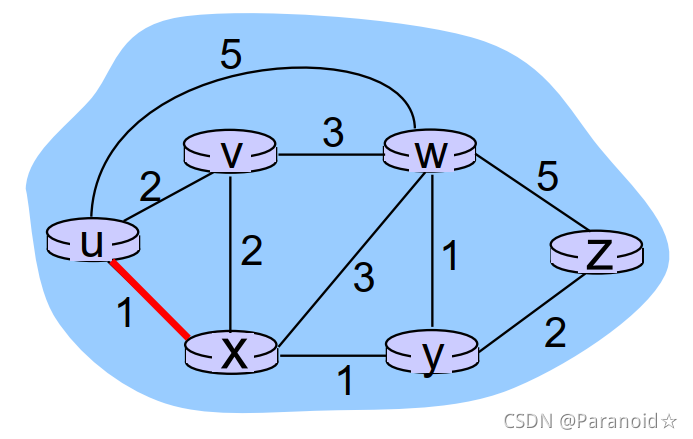
每个结点的作用:
x维护距离向量(DV): Dx = [Dx(y): y ? N ]
结点x:已知到达每个邻居的费用: c(x,v),维护其所有邻居的距离向量: Dv = [Dv(y): y ? N ]
根据B-F方程:
du(z) = min { c(u,v) + dv(z), c(u,x) + dx(z), c(u,w) + dw(z) }
= min {2 + 5,1 + 3,5 + 3}
= 4
最短路径由该结点的到邻居的最小费用再加上邻居的最短距离向量
特点:
(1)异步迭代: 引发每次局部迭代的因素:局部链路费用改变 和 来自邻居的DV更新
(2)分布式: 每个结点只当DV变化时才通告给邻居,邻居在必要时(其DV更新后发生改变)再通告它们的邻居
每个结点必做的工作
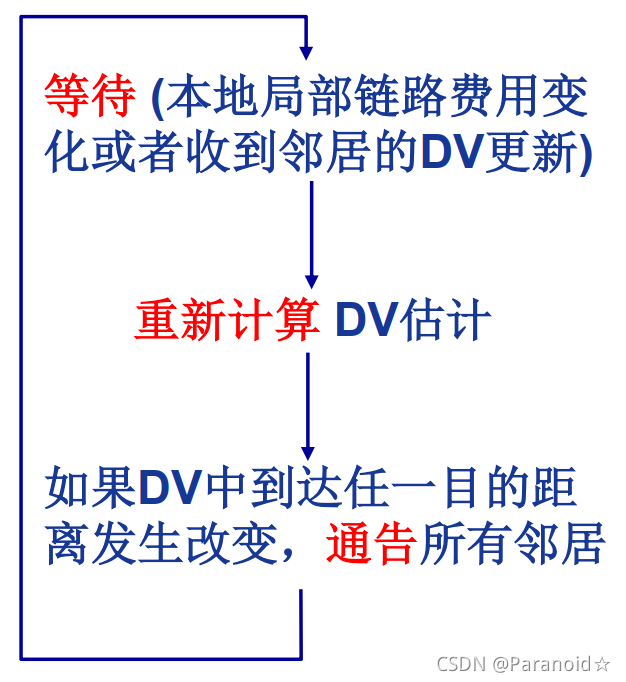
链路费用变化:
结点检测本地链路费用变化,更新路由信息,重新计算距离向量,如果DV改变,通告所有邻居
(1)当路径费用减小
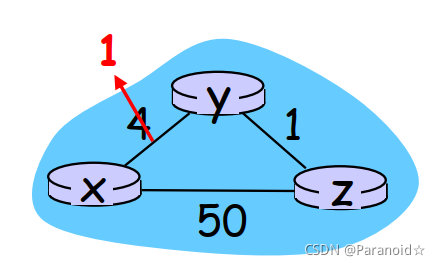
更新过程:
t0 : y检测到链路费用改变 ,更新DV,通告其邻居
t1 : z收到y的DV更新,更新其距离向量表,计算到达x的最新最小费用,更新其DV,并发送给其所有邻居
t2 : y收到z的DV更新, 更新其距离向量表,重新计算y的DV,
未发生改变,不再向z发送DV.
路径费用减小传播速度较快
(2)当路径费用增加
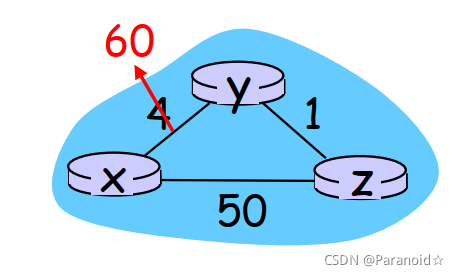
会产生无穷计数问题,传播速度慢
跟新过程:
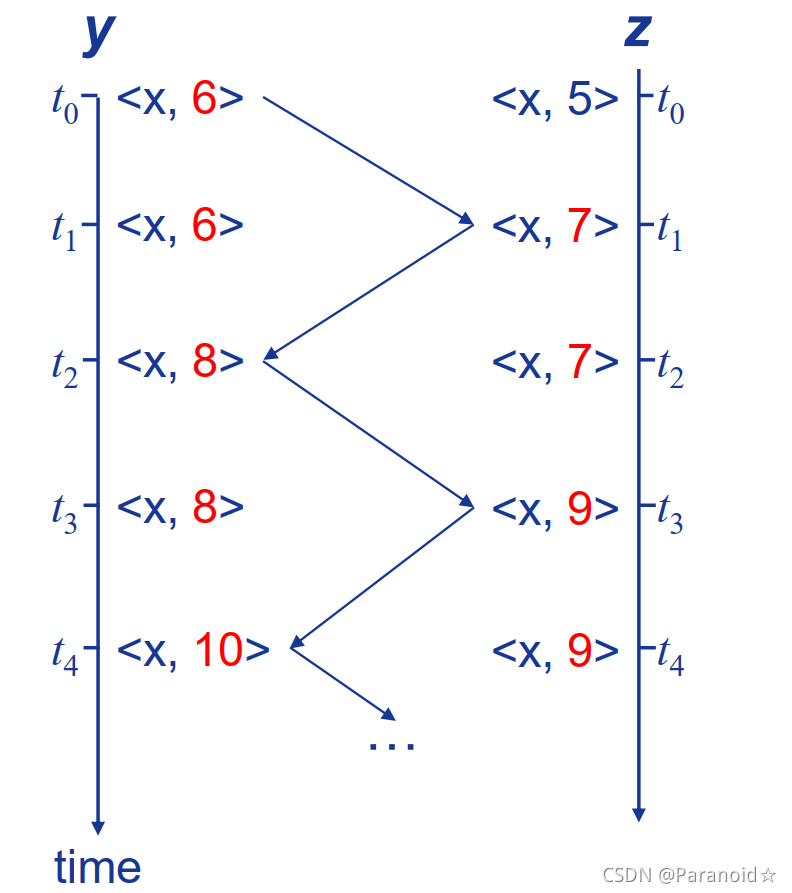
解决办法:
1.毒性逆转(poisoned reverse): 如果一个结点(Z)到达某目的(X)的最小费用路径是通过某个邻居(Y),则:通告给该邻居结点到达该目的的距离为无穷大
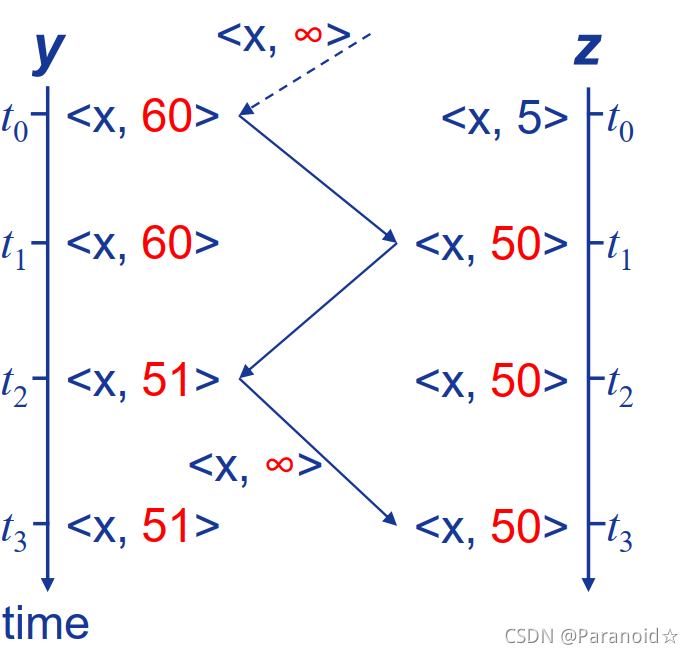
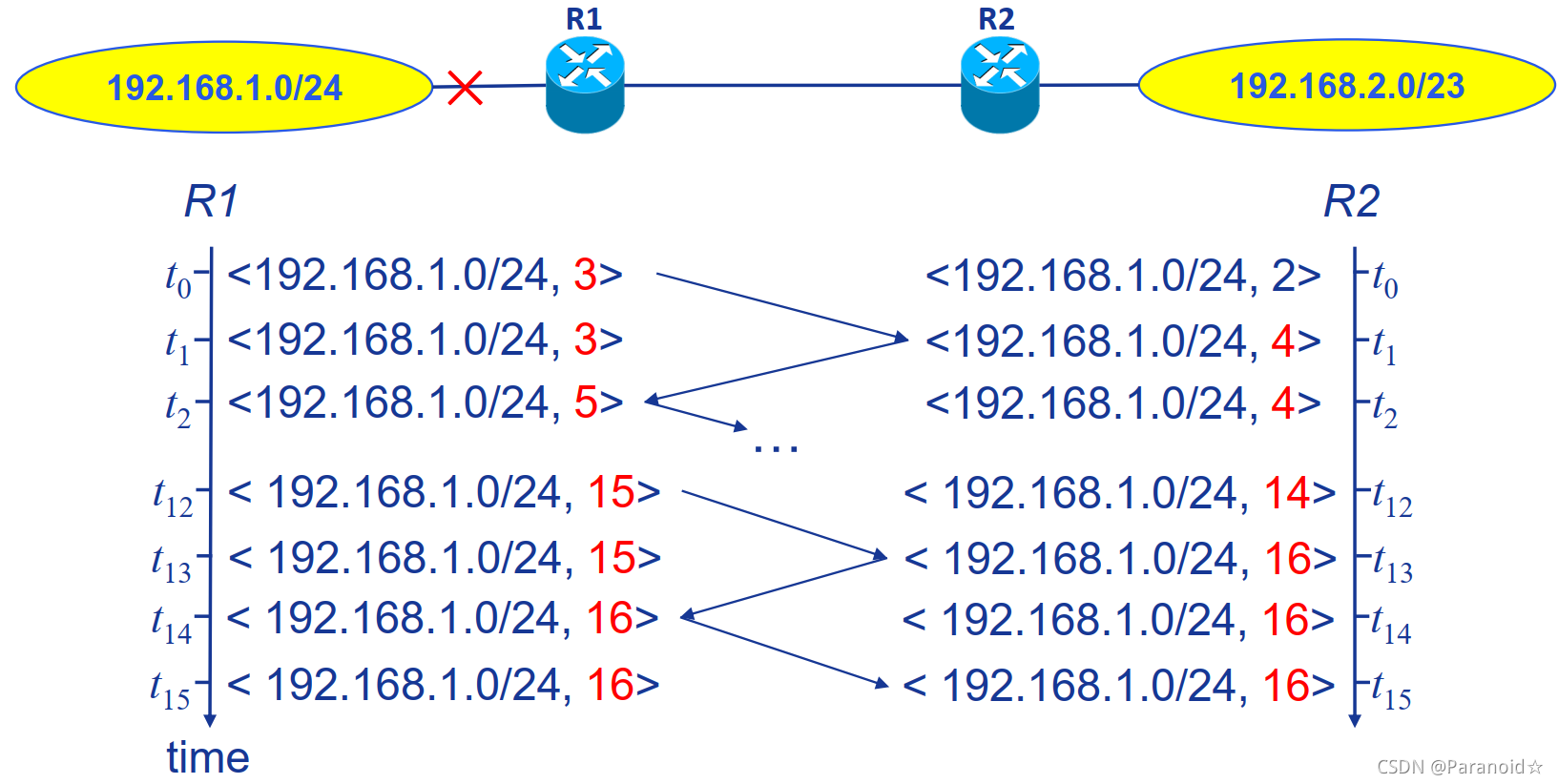
2.定义最大度量(maximum metric): 定义一个最大的有效费用值,如15跳步, 16跳步表示∞
总结
提示:这里对文章进行总结: