文章目录
- 前言
- 一、神经网络的提出
- 二、神经网络模型
-
- 1.模型引入
- 2.模型案例
- 三、多类分类
- 总结
前言
一、神经网络的提出
线性回归和逻辑回归都只适合用于特征比较少的情况,当特征太多时,
计算的负荷会非常大
eg: 训练一个模型来识别视觉对象, 识别一张图片上是否是一辆汽车

方法:利用大量汽车的图片和非汽车的图片,然后利用图片上像素的值(饱和度或亮度)来作为特征,只选用灰度图片,每个像素则只有一个值,可以选取图片上的两个不同位置上的两个像素,然后训练一个逻辑回归算法利用这两个像素的值来判断图片上是否是汽车

假使采用的都是 50x50 像素的小图片,并且将所有的像素视为特征,则会有2500 个特征,如果要进一步将两两特征组合构成一个多项式模型,则会有约接近 3 百万个特征。普通的逻辑回归模型,不能有效地处理这么多的特征,这时候就需要神经网络
二、神经网络模型
1.模型引入
为了构建神经网络模型,需要首先思考大脑中的神经网络是怎样的?
每一个神经元被认为是一个处理单元/神经核( processing unit/Nucleus),它含有许多输入/树突( input/Dendrite),并且有一个输出/轴突( output/Axon)。神经网络是大量神经元相互链接并通过电脉冲来交流的一个网络

神经元利用微弱的电流进行沟通,神经元把自己的收到的消息进行计算,并向其他神经元传递消息
神经网络模型建立在大量神经元之上,每一个神经元又是一个学习模型,神经元也叫激活单元(activation uni)t采纳一些特征作为输出,并且根据本身的模型提供一个输出
下图是一个以逻辑回归模型作为自身学习模型的神经元示例,在神经网络中,参数又称为权重( weight)

eg: 多层神经网络

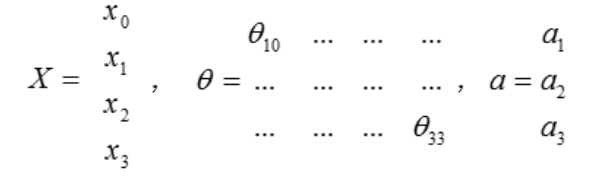
??(?) 代表第? 层的第 ? 个激活单元。?(?)代表从第 ? 层映射到第? + 1 层时的权重的矩阵, 其尺寸为:以第 ? + 1层的激活单元数量为行数,以第 ? 层的激活单元数加一为列数的矩阵
?(1)代表从第一层映射到第二层的权重的矩阵,尺寸为 3*4
激活单元和输出分别表达为:

上面只是将特征矩阵中的一行(一个训练实例)喂给了神经网络,我们需
要将整个训练集都喂给神经网络算法来学习模型
把?, ?, ? 分别用矩阵表示, 可以得到? ? ? = ?,每一个?都是由上一层所有的?和每一个所对应?的决定的
从左到右的算法称为前向传播算法( FORWARD PROPAGATION )
引入向量,利用向量化的方法计算
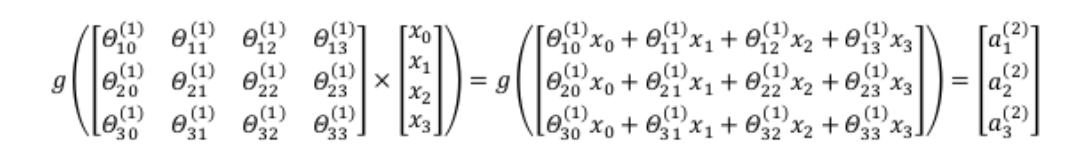

令 ?(2) = ?(1)?,则 ?(2) = ?(?(2)) ,计算后添加 ?0(2) = 1, 计算输出的值为:

令 ?(3) = ?(2)?(2),则 ??(?) = ?(3) = ?(?(3))
如果要对整个训练集进行计算,需要将训练集特征矩阵进行转置,使得同一个实例的特征都在同一列里,即:
?(2) = ?(1) × ?? ,?(2) = ?(?(2))
将左半部分遮住,右半部分就是?0, ?1, ?2, ?3,按照 Logistic Regression 的方式输出??(?):
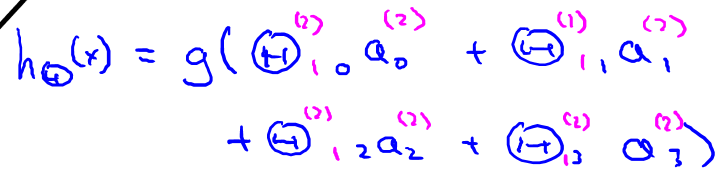
神经网络就像是 logistic regression,只不过把 logistic regression 中的输入向量[?1 ? ?3] 变成了中间层的[?1(2) ? ?3(2)]
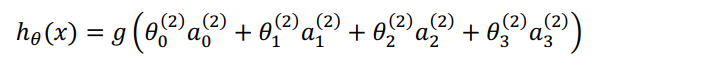
把?0, ?1, ?2, ?3看成更为高级的特征值,?0, ?1, ?2, ?3的进化体,并且它是由 ?与决定的,因为是梯度下降的,所以?是变化的,并且变得越来越厉害,这些更高级的特征值远比仅仅将 ?次方厉害,也能更好的预测新据。这就是神经网络相比于逻辑回归和线性回归的优势
2.模型案例
在逻辑回归中,被限制为使用数据中的原始特征?1, ?2, . . . , ??,虽然可以使用一些二项式项来组合这些特征,但是仍然受到这些原始特征的限制
在神经网络中,原始特征只是输入层,在上面的eg,第三层就是输出层做出的预测利用的是第二层的特征,而非输入层中的原始特征,可以认为第二层中的特征是神经网络通过学习后自己得出的一系列用于预测输出变量的新特征
从本质上讲,神经网络能够通过学习得出其自身的一系列特征
(1)单层神经元
利用单层神经元(无中间层)来表示逻辑运算逻辑与(AND)、逻辑或(OR)
(1)AND函数

其中?0 = ?30, ?1 = 20, ?2 = 20 ,则输出函数??(?)即为:
??(?) = ?(?30 + 20?1 +20?2),g函数是sigmod 函数

AND 函数: ??(?) ≈ x1AND?x2
(2)OR 函数

??(?) = ?(?10 + 20?1 +20?2),真值表如下:

(2)多次神经元
用神经网络表示二元逻辑运算符( BINARY LOGICAL OPERATORS)
当输入特征为布尔值( 0 或 1)时,可以用一个单一的激活层可以作为二元逻辑运算符,为了表示不同的运算符,只需要选择不同的权重即可

利用神经元来组合成更为复杂的神经网络以实现更复杂的运算。要实现 XNOR 功能(输入的两个值必须一样,均为 1 或均为 0),即:
XNOR = (x1?AND?x2)?OR((NOT?x1)AND(NOT?x2))
首先构造一个能表达(NOT?x1)AND(NOT?x2)部分的神经元:

然后将表示 AND 的神经元和表示(NOT?x1)AND(NOT?x2)的神经元以及表示 OR 的神经元进行组合:

就能实现 XNOR 运算符功能的神经网络
三、多类分类
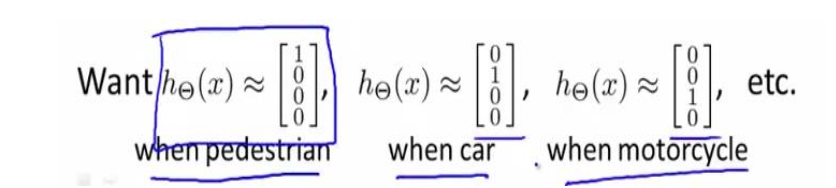
很多情况下,我们当不止有两种分类时,要训练一个神经网络算法来识别路人、汽车、摩托车和卡车,在输出层应该有 4 个值。例如,第一个值为 1 或 0 用于预测是否是行人,第二个值用于判断是否为汽车…
输入向量?有三个维度,两个中间层,输出层 4 个神经元分别用来表示 4 类,每一个数据在输出层都会出现[? ? ? ?]?,且?, ?, ?, ?中仅有一个为 1,表示当前类

神经网络算法的输出结果为四种可能情形之一: