等价关系——离散数学_综合

定义：集合S上的关系≡,称为S上为等价关系，当且仅当它在S上是对称的，自反的，传递的。
例如：

x=x
x=y意味着y=x
x=y且y=z意味着x=z
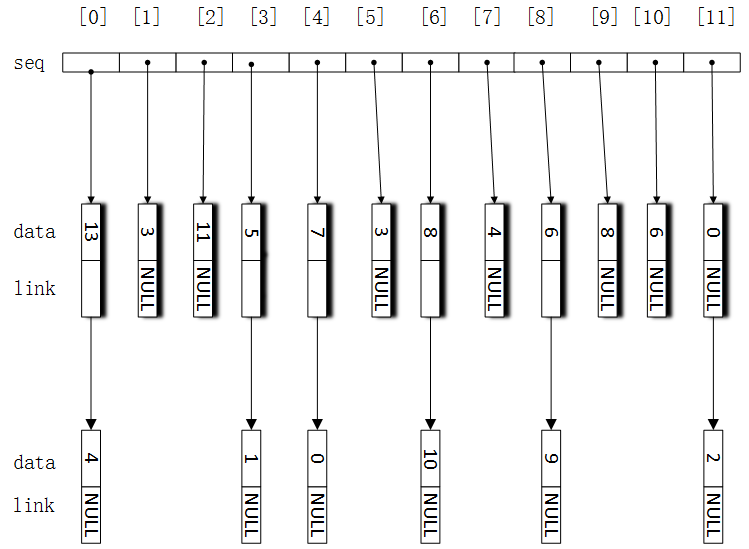
可以使用等价关系将集合S划分为等价类，S的两个元素x和y属于同一等价类，当且仅当≡，例如，有12个编号为0至11元素：
0≡4,3≡1,6≡10,8≡9,7≡4,6≡8,3≡5,2≡11,11≡0
那么根据关系≡的自反性，对称性和传递性的结果，可以归为以下几个等价类：
{0, 2, 4, 7, 11};{1, 3, 5};{6, 8, 9, 10}.
如果用二维数组去表示其等价关系，不仅会浪费大量空间，还需相当的时间去寻找两个等价元素之间的第三个等价元素。那么我们可以考虑用链表来去查找等价类的元素，来减少时间和空间复杂度，其用链表设计查找等价类的结构如图：

代码实现：

#include <iostream>
#include<stdlib.h>
#include<stdio.h>
//等价关系最大范围(0-MAX_SIZE)其中不包括MAX_SIZE
#define MAX_SIZE 24
#define IS_FULL(ptr) (!(ptr))
//标记输出过
#define FALSE 0
//标记没有输出过
#define TRUE 1
typedef struct node *node_pointer;
//存储结构
struct node
{int data;node_pointer link;
};
using namespace std;
int main()
{//存储元素是否输出过的标记int out[MAX_SIZE];//每个等价元素链表的头结点node_pointer seq[MAX_SIZE];node_pointer x,y,top;int i,j,n;//输入其元素范围[0,n)printf("Enter the size(<=%d) ",MAX_SIZE);scanf("%d",&n);//初始化操作for(i=0;i<n;i++){out[i]=TRUE;seq[i]=NULL;}printf("Enter a pair of numbers (-1 -1 to quit):" );//循环输入等价关系的元素对scanf("%d%d",&i,&j);while(i>=0){x=(node_pointer)malloc(sizeof(node));if(IS_FULL(x)){fprintf(stderr,"the memory is full\n");exit(1);}//插入到第i个链表的前端x->data=j;x->link=seq[i];seq[i]=x;x=(node_pointer)malloc(sizeof(node));if(IS_FULL(x)){fprintf(stderr,"the memory is full\n");exit(1);}//插入到第j个链表的前端x->data=i;x->link=seq[j];seq[j]=x;printf("Enter a pair of numbers (-1 -1 to quit):" );scanf("%d%d",&i,&j);}for(i=0;i<n;i++){//判断是否输出if(out[i]){printf("\nNew class:%5d",i);out[i]=FALSE;//查找剩下的等价结点x=seq[i];top=NULL;for(;;){//输出链表的等价元素while(x){j=x->data;if(out[j]){printf("%5d",j);out[j]=FALSE;//使其链表结点的指针方向反向y=x->link;x->link=top;top=x;x=y;}else{x=x->link;}}if(!top) break;//查找第top->data个等价链表的元素x=seq[top->data];top=top->link;}}} 
}

分析：seq和out初始化的时间开销为O(n),输入等价对时，其时间开销是常量，故该阶段为的时间总开销为O(m+n),在第二阶段中，每个节点至多放入链栈一次，由于只有2m个节点，并且for循环n次，故该阶段的时间开销是O(m+n),因此总的计算时间开销是O(m+n).其算法空间的开销是O(m+n).