GBDT(分类,回归(线性/非线性))
1.原理简介
2.原理:回归/分类
3.正则化
4.优缺点
1.原理简介:(gradient boosting decision tree)
(形式+迭代目标+拟合方法)
GBDT就是boosting框架+任意损失函数+CART回归树模型;他关注的是残差值,迭代目标是找到一个CART回归树模型的弱学习器,让损失函数最小(找决策树,让损失最小);损失函数拟合方法:通过用损失函数的负梯度来拟合损失进而拟合一个CART回归树,将残差向梯度方向减小。
弱分类器要求:对弱分类器的要求一般是足够简单,并且是低方差和高偏差的。因为训练的过程是通过降低偏差来不断提高最终分类器的精度
GBDT应用:搜索排序、点击率预估
实例

2.原理:回归/分类
回归
(1)原理:初始化弱学习器,T轮迭代,每轮都去拟合负梯度,得到强学习器

(2)损失函数(回归)
1)均方差:L(y,f(x))=(y?f(x))2
2)绝对损失:L(y,f(x))=|y?f(x)|
对应负梯度误差:sign(yi?f(xi))
3)Huber损失:对靠近中心的用均方差,对远离中心的用绝对损失。界限用分位数点度量
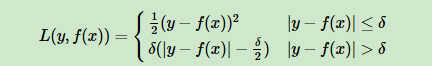
对应负梯度误差:
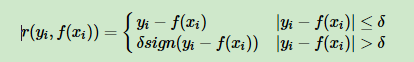
4)分位数损失:

其中θ为分位数,需要我们在回归前指定
对应负梯度误差:
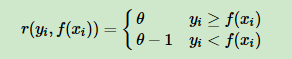
对Huber损失和分位数损失,主要用于健壮回归,也就是减少异常点对损失函数的影响。
分类
(1)原理:GBDT的分类算法思想和回归一样,但是由于样本输出不是连续值而是离散值,导致无法直接从输出类别去拟合类别输出的误差
解决方法:使用指数损失/对数似然损失函数
(2)损失函数(分类)
1)指数损失:退化成adaboost算法 L(y,f(x))=exp(?yf(x))
2)对数似然损失:用类别的预测概率值和真实概率值的差来拟合损失
对数似然损失函数分类:
1)二元GBDT分类算法——类似二元LR

除负梯度计算和叶子节点的最佳负梯度拟合的线性搜索,二元GBDT分类,回归算法过程相同。
2)多元GBDT分类算法——类似多元LR

除负梯度计算和叶子结点的最佳负梯度拟合的线性搜索,多元GBDT分类回归算法过程相同
4.正则化
(1)步长

(2)子采样比例subsample
GBDT的子采样和RF的不一样,GBDT不放回,RF有放回,取值=1时就是全部样本都用等于没有子采样,取值<1时,可减少方差(防止过拟合),但会增加偏差。推荐取[0.5,0.8]
(3)对CART回归树进行剪枝
5.优缺点
优点:
(1)可灵活处理各种类型的数据,包括连续值和离散值
(2)使用健壮的损失函数,如Huber损失函数,对异常值的鲁棒性非常强
(3)非线性变换比较多,表达能力强,不需要做复杂的特征工程
缺点:
(1)弱学习器直接存在依赖关系,难以并行训练数据
(2)由于GBDT很容易出现过拟合的问题,所以推荐的GBDT深度不要超过6,而随机森林可以在15以上。
(3)计算复杂度高
(4)不适合高维稀疏特征
GBDT问题
1.GBDT如何选特征?(其实就是CART Tree生成的过程)
gbdt选择特征的过程就是CART Tree生成的过程。
关键:如何选特征m+如何选特征切分点j
在m个特征中选出一个特征j做完二叉树的第一个节点,对特征j的值选一个切分点m,大于m为一类,小于m为另一类
方法:暴力搜索
遍历所有特征,然后对每个特征遍历他所有可能的切分点,找到最优特征m的最优切分点j。找到使下式最小的m和j:
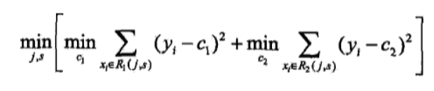
2. gbdt 如何构建特征 ?
将样本输入到GBDT生成的树中,所有树的叶子结点可以构建一个向量,输入样本可以获得一个关于叶子结点的0-1向量,将这个向量作为该样本的组合特征,和原来的特征一起输入到逻辑回归当中训练
其实说gbdt 能够构建特征并非很准确,gbdt 本身是不能产生特征的,但是我们可以利用gbdt去产生特征的组合。在CTR预估中,工业界一般会采用LR去进行处理, LR本身是适合处理线性可分的数据,如果我们想让逻辑回归处理非线性的数据,其中一种方式便是组合不同特征,增强逻辑回归对非线性分布的拟合能力。
3.gbdt 如何用于分类?
gbdt核心是每轮的训练是在上一轮的训练的残差基础之上进行训练的,残差就是当前模型的负梯度值 。这要求每轮迭代时,弱分类器的输出的结果相减是有意义的,即残差相减是有意义的。但选用的弱分类器是分类树时,类别相减是没有意义的。
方法:K分类,同时训练K棵树
具体流程:(如K=3)
(1)样本x属于第二类,用向量[0,1,0]表示
(2)第一棵树样本x的第一类,输入为(x,0),第二棵树样本x的第二类,输入为(x,1),第三棵树样本x的第三类,输入为(x,0),按CART的生成得出三棵树和对x类别的预测值f1(x),f2(x),f3(x),仿照多分类LR,使用softmax 产生概率,则属于类别1的概率:

对类别1求残差y11(x)=0?p1(x);类别2残差y22(x)=1?p2(x);类别3残差y33(x)=0?p3(x)。
(3)然后开始第二轮训练,迭代
针对第一类 输入为(x, y11(x)), 针对第二类输入为(x,y22(x)), 针对第三类输入为 (x,y33(x)).继续训练出三颗树。一直迭代M轮,每轮构建3颗树。当K =3,应该有三个式子
F1M(x)=∑C1mI
F2M(x)=∑C2mI
F3M(x)=∑C3mI
(4)训练完毕以后,新来一个样本 x1 ,我们需要预测该样本的类别的时候,便可以有这三个式子产生三个值,f1(x),f2(x),f3(x),样本属于某个类别c的概率为
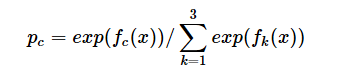
4.gbdt 通过什么方式减少误差 ?
每棵树都是在拟合当前模型的预测值和真实值之间的误差,GBDT是通过不断迭代来使得误差见小的过程。
5 gbdt 如何加速训练?(不确定)
小数据集使用True,可加快训练,是否预排序,预排序可以加速查找最佳分裂点
6.gbdt的参数有哪些,如何调参 ?
GBDT参数(最大迭代器个数、步长、子采样比例)
(1)第一类Miscellaneous Parameters: Other parameters for overall functioning. 没啥用
(2)第二类:Boosting Parameters: These affect the boosting operation in the model.
n_estimators 最大弱学习器的个数,太小欠拟合,太大过拟合
learning_rate 学习率,太大过拟合,一般很小0.1,和n_estimators一起调
subsample 子采样,防止过拟合,太小欠拟合。GBDT中是不放回采样
(3)第三类:Tree-Specific Parameters: These affect each individual tree in the model.
max_features 最大特征数
max_depth 最大树深,太大过拟合
min_samples_split 内部节点再划分所需最小样本数,越大越防过拟合
min_weight_fraction_leaf 叶子节点最小的样本权重和。如果存在较多样本有缺失值,或者分类树样本的分布类别偏差很大,就会引入样本权重,这时我们就要注意这个值了。越大越防过拟合
max_leaf_nodes:最大叶子节点数 ,太大过拟合
min_impurity_split:节点划分最小不纯度
presort:是否对数据进行预分类,以加快拟合中最佳分裂点的发现。默认False,适用于大数据集。小数据集使用True,可以加快训练。是否预排序,预排序可以加速查找最佳分裂点,对于稀疏数据不管用,Bool,auto:非稀疏数据则预排序,若稀疏数据则不预排序
GBDT调参
(1)首先使用默认的参数,进行数据拟合;
(2)从步长(learning rate)和迭代次数(n_estimators)入手;一般来说,开始选择一个较小的步长来网格搜索最好的迭代次数。这里,可以将步长初始值设置为0.1。对于迭代次数进行网格搜索;
(3)接下来对决策树的参数进行寻优
(4)首先我们对决策树最大深度max_depth和内部节点再划分所需最小样本数min_samples_split进行网格搜索。[min_samples_split暂时不能一起定下来,因为这个还和决策树其他的参数存在关联]
(5)接着再对内部节点再划分所需最小样本数min_samples_split和叶子节点最少样本数min_samples_leaf一起调参;做到这里,min_samples_split要做两次网格寻优,一次是树的最大深度max_depth,一次是叶子节点最少样本数min_samples_leaf。
[具体观察min_samples_split的值是否落在边界上,如果是可以进一步寻优]
(6)继续对最大特征数max_features进行网格搜索。做完这一步可以看看寻找出的最优参数组合给出的分类器的效果。
(7)可进一步考虑对子采样的比例进行网格搜索,得到subsample的寻优参数
(8)回归到第2步调整设定的步长(learning rate)和迭代次数(n_estimators),注意两者的乘积保持不变,这里可以分析得到:通过减小步长可以提高泛化能力,但是步长设定过小,也会导致拟合效果反而变差,也就是说,步长不能设置的过小。
7.GBDT中为什么要用负梯度来代替残差计算?
关键:损失函数收敛到最小
1.负梯度的方向可证,模型优化下去一定会收敛
2.对于一些损失函数来说最大的残差方向,并不是梯度下降最好的方向。boosting的本质是通过累加各个学习器使得损失函数减小,而不是使训练样本拟合的更好
3.在每一轮迭代中需要对损失函数的负梯度构造回归树,而不是对“残差”构造回归树,这样才能保证GBDT最终能收敛到一个强学习器,使损失函数最小。如果直接对“残差”构造回归树的话,最终损失函数能否收敛到最小值就不一定了。
4.拓展到更复杂的损失函数:其实除了均方误差的情况一阶导是残差外,其他的情况没有残差的概念,GBDT每一轮拟合的都是损失函数负梯度。使用梯度计算代替残差的主要原因是为了将GBDT拓展到更复杂的损失函数中。当损失函数形式简单,可以认为模型输出值等于实际值时损失函数最小,但当损失函数加入正则项(决策树的正则项主要是叶子节点个数,在xgboost中还与叶子节点的取值有关)后,并非在时损失函数取得最小值,所以我们需要计算损失函数的梯度,而不能直接使用模型来计算残差。
采用Square loss为损失函数时,负梯度和残差相等。当采用Absolute loss/Huber loss等其它损失函数时,负梯度只是残差的近似
8.为什么GBDT不适合使用高维稀疏特征?
1.时间慢
特征太多,GBDT不一定跑的动,即使可以跑也会耗费很长时间。主要是由于树模型在分支时的特征选择相当耗时,尤其是当特征量很大的时候。其次由于GBDT的boosting算法,需要构建多棵CART树,虽然对于弱分类器CART树而言,不需要很深,但弱分类器的构建往往在开始的时候是很慢的。
2.特征浪费
树的分割往往只考虑了少量的特征,大部分的特征都用不到。boosting过程需要迭代多棵CART树,每次树的构建可能使用的特征都类似,所以高维稀疏特征会造成大量特征的浪费。
9.GBDT里的G代表什么,体现在哪里?
Gradient,用梯度下降的负方向去拟合残差
10.GBDT的适用范围
几乎可用于所有回归问题(线性/非线性),相对LR仅能用于线性回归,GBDT的适用面非常广,也可用于二分类问题(设定阈值,大于阈值为正例,反之为负例)。
11 GBDT如何进行正则化?
(1)与Adaboost类似的正则项,即learning_rate
(2)子采样比例subsample
(3)针对基学习器的正则化剪枝操作
12.GBDT对异常值敏感吗?
GBDT在不使用一些健壮的损失函数的情形下,对于异常值实际上是极为敏感的。如果使用一些健壮的损失函数,如Huber以及分位数Quantile损失函数则可以改善这个状况。
13.从GBDT的算法模型来理解为什么GBDT对异常值相当敏感?
GBDT每一次拟合上一次弱回归树的负梯度。如果样本中存在异常值。则每一次的负梯度往往都会被异常值给放大(仔细回想回归树的最优分裂点选取准则以及子节点的预测值计算)。直观来想,其实很好理解,模型是无法判断这个值是不是异常值的,它只会机械的让模型去充分拟合样本,如果存在异常值,模型依旧希望可以较为充分的拟合它(使得损失函数最低),此时整个模型的预测就会因为一个极端的预测值而被带偏。对于正常样本的预测能力就会大大降低了。
14.GBDT如何减少异常点的影响?
1) 使用健壮的损失函数,比如Huber损失函数和分位数(Quantile)损失函数;
2) 增加正则化项;
3) 采用无放回的子采样。
15.RF和GBDT对于异常点的鲁棒性比较?
对于异常点的鲁棒性,RF要比GBDT好的多。主要原因是GBDT的模型在迭代过程中较远的异常点残差往往会比正常点大,导致最终建立的模型出现偏差。一般的经验是,异常点少的样本集GBDT表现更加优秀,而异常点多的样本集,随机森林表现更好。