AcWing 1212. 地宫取宝四维线性dp_综合

AcWing 1212. 地宫取宝

X 国王有一个地宫宝库，是 n×m 个格子的矩阵，每个格子放一件宝贝，每个宝贝贴着价值标签。

地宫的入口在左上角，出口在右下角。

小明被带到地宫的入口，国王要求他只能向右或向下行走。

走过某个格子时，如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它（当然，也可以不拿）。

当小明走到出口时，如果他手中的宝贝恰好是 k 件，则这些宝贝就可以送给小明。

请你帮小明算一算，在给定的局面下，他有多少种不同的行动方案能获得这 k 件宝贝。

输入格式
第一行 3 个整数，n,m,k，含义见题目描述。

接下来 n 行，每行有 m 个整数 Ci 用来描述宝库矩阵每个格子的宝贝价值。

输出格式
输出一个整数，表示正好取 k 个宝贝的行动方案数。

该数字可能很大，输出它对 1000000007 取模的结果。

数据范围
1≤n,m≤50,
1≤k≤12,
0≤Ci≤12
输入样例1：

2 2 2
1 2
2 1

输出样例1：

输入样例2：

2 3 2
1 2 3
2 1 5

输出样例2：

这道题呀，刚开始我是想到了用三维dp存 $d p [k] [i] [j]$
i，j表示运行到{i,j}这个点，k表示背包有k个物品。确实没有做出来，于是看了yxc的视频然后了解到了一个四维的做法，看来思维要大胆一点，万物皆可dp
看一下y总的思路。
在这里插入图片描述

解题思路：这道题可以用四维DP解决，由于接触DP没多久，对于我来说确实是一个挑战，但是经过大半天的挣扎，算是把这道题的思路
整理出来了，这里我模仿yxc的DP分析思路：用集合的思想考虑DP
第一个要想清楚的就是，要取得当前格子的物品，这个物品必须比当前所拥有的物品都大，所以有一个性质：后面拿的物品
比前面的物品大
然后画出以下的分析图：

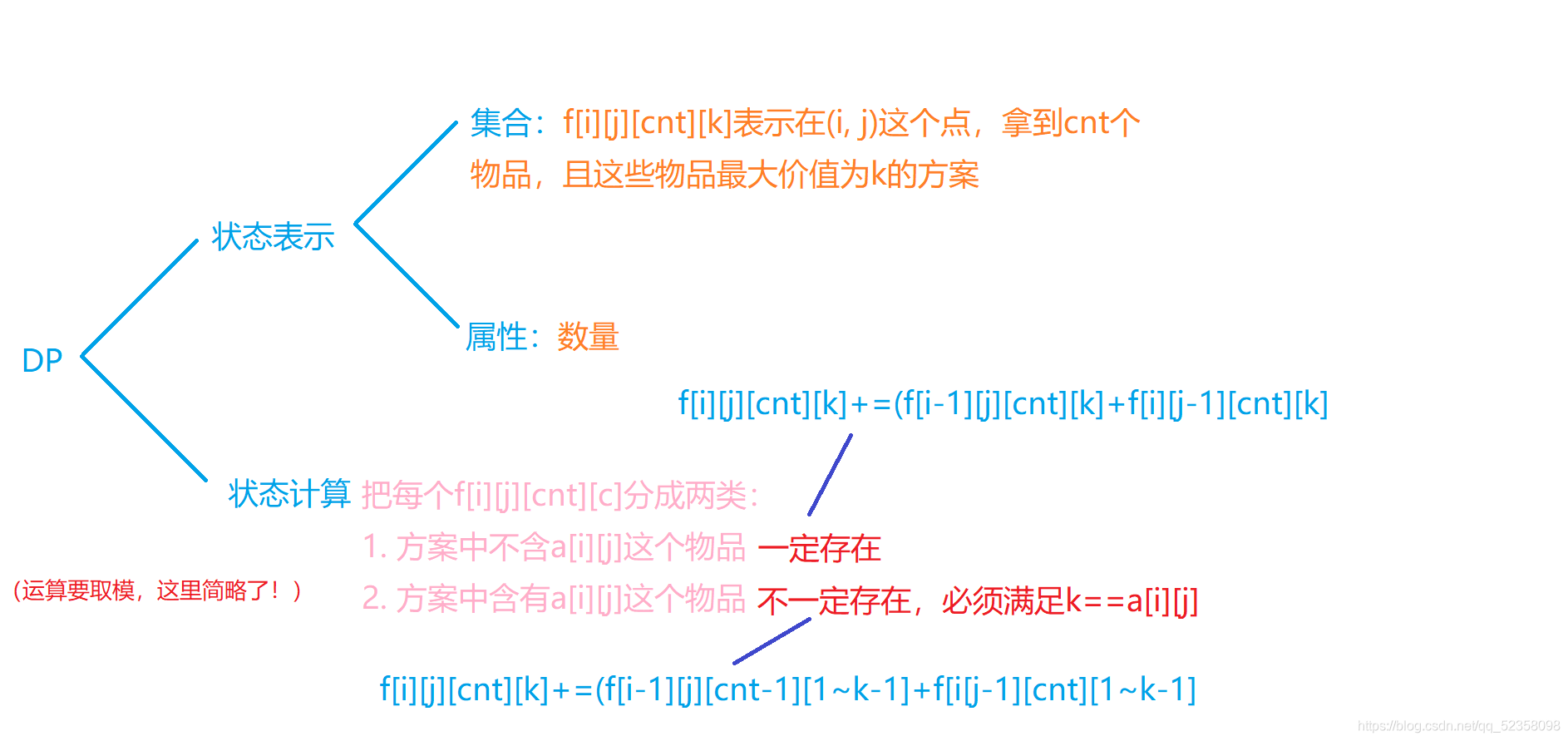
在这里插入图片描述


难点在于状态计算部分，联想到01背包问题，对于每个物品，都有取或不取两种选择，而不取是肯定可以的，要取的话，要
满足背包能放下这个条件
这里也一样，对于每个物品，都可以不选，也就是直接从上一步转移状态过来，但是如果要取得(i,j)(i,j)位置的物品，
就必须满足当前的kk和a[i][j]a[i][j]相等，因为上面分析过了，如果现在取了a[i][j]a[i][j]，那么它肯定是现在所
有物品最大的，这和我们一开始四维数组的定义是对应的
在具体的状态转移中，如果不选，就直接从上一步完完整整地把状态cntcnt和kk转移过来；如果选，那上一步就应该选了
cnt?1cnt?1个物品，而且上一步身上所有物品最大值只能是1…k?11…k?1，把这些状态的方案数累加，就可以成为选择当
前物品的条件
注意事项：因为这道题的所有物品价值范围是0…120…12，可以把他们全部都递增，范围就变成了1…131…13，因为我们记录的是方案
数，只关心各个物品之间的大小关系，具体数值不影响答案，但是这样的做法可以把00作为一个特殊边界来处理
整个过程不理解的话，可以用纸笔模拟一下，看看每个状态的数值应该是多少作者：Daniel丶y
链接：https://www.acwing.com/solution/content/7116/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

大佬的思路很清晰，根据这位大佬的思路，我写出了相应的代码。
代码如下

#include<iostream>
#include<algorithm>using namespace std;const int N=55,M=15,MOD=1000000007;int dp[N][N][13][14];//开数组要注意一下开大一点
int wi[N][N];int main(void)
{
    int n,m,k;cin>>n>>m>>k;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)cin>>wi[i][j],wi[i][j]++;//注意加1，因为价值为0的也表示选了dp[1][1][1][wi[1][1]]=1;dp[1][1][0][0]=1;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){
    if(i==1&&j==1) continue;//已经排好了else{
    for(int a=0;a<=k;a++)for(int b=0;b<=13;b++){
    int &val=dp[i][j][a][b];//类似于杨老师的照相序列，介绍代码复杂度val=(val+dp[i-1][j][a][b])%MOD;//未选val=(val+dp[i][j-1][a][b])%MOD;//未选if(b==wi[i][j]&&a)//只有背包有东西并且当前的价值为坐标的价值的时候。{
    for(int p=0;p<b;p++){
    val=(val+dp[i-1][j][a-1][p])%MOD;val=(val+dp[i][j-1][a-1][p])%MOD;}}}}}int res=0;for(int i=1;i<=13;i++)  res=(res+dp[n][m][k][i])%MOD;//y总的代码从1开始，表示从来没有选过，我改成从1开始了cout<<res;
}

AcWing 1212. 地宫取宝 四维线性dp

AcWing 1212. 地宫取宝四维线性dp