题:
The 2050 volunteers are organizing the “Run! Chase the Rising Sun” activity. Starting on Apr 25 at 7:30 am, runners will complete the 6km trail around the Yunqi town.
There are n+1 checkpoints on the trail. They are numbered by 0, 1, …, n. A runner must start at checkpoint 0 and finish at checkpoint n. No checkpoint is skippable — he must run from checkpoint 0 to checkpoint 1, then from checkpoint 1 to checkpoint 2 and so on. Look at the picture in notes section for clarification.
Between any two adjacent checkpoints, there are m different paths to choose. For any 1≤i≤n, to run from checkpoint i?1 to checkpoint i, a runner can choose exactly one from the m possible paths. The length of the j-th path between checkpoint i?1 and i is bi,j for any 1≤j≤m and 1≤i≤n.
To test the trail, we have m runners. Each runner must run from the checkpoint 0 to the checkpoint n once, visiting all the checkpoints. Every path between every pair of adjacent checkpoints needs to be ran by exactly one runner. If a runner chooses the path of length li between checkpoint i?1 and i (1≤i≤n), his tiredness is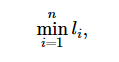
i. e. the minimum length of the paths he takes.
Please arrange the paths of the m runners to minimize the sum of tiredness of them.
Input
Each test contains multiple test cases. The first line contains the number of test cases t (1≤t≤10000). Description of the test cases follows.
The first line of each test case contains two integers n and m (1≤n,m≤100).
The i-th of the next n lines contains m integers bi,1, bi,2, …, bi,m (1≤bi,j≤10^9).
It is guaranteed that the sum of n?m over all test cases does not exceed 10^4.
Output
For each test case, output n lines. The j-th number in the i-th line should contain the length of the path that runner j chooses to run from checkpoint i?1 to checkpoint i. There should be exactly m integers in the i-th line and these integers should form a permuatation of bi,1, …, bi,m for all 1≤i≤n.
If there are multiple answers, print any.
Example
input
2
2 3
2 3 4
1 3 5
3 2
2 3
4 1
3 5
output
2 3 4
5 3 1
2 3
4 1
3 5
Note
In the first case, the sum of tiredness is min(2,5)+min(3,3)+min(4,1)=6.
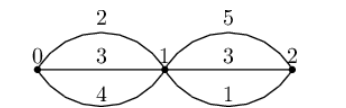
In the second case, the sum of tiredness is min(2,4,3)+min(3,1,5)=3.
题意:
m个跑步者,n条路径,求疲劳度最小化。
思路:
用一个数组把所有的数都放进去从小到大排序并标记前m个,使得每一列都有一个被标记的数。
ps:这题题目都看错了QAQ,而且我还对着理解错了的题意纠结了好久,还是最后sj大佬给我讲解的时候我才发现理解错了,又是被自己蠢到的一天。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<memory.h>
using namespace std ;#define bug(a) cout << "*" << a << endl ;typedef long long ll ;
const int N = 105 ;ll v[N][N] , b[N][N] , a[N][N] ;
bool vis[N][N] ;int t , n , m ;struct node
{
int x , y ;ll z ;
}mi[10005] ;bool cmp( node k , node l )
{
return k.z < l.z ;
}int main()
{
ios::sync_with_stdio(false) ;cin.tie(0) ;cout.tie(0) ;cin >> t ;while( t-- ){
cin >> n >> m ;ll cnt = 0 ;ll q = 0 ;memset( mi , 0 , sizeof mi ) ;memset( v , 0 , sizeof v ) ;memset( vis , 0 , sizeof vis ) ;memset( a , 0 , sizeof a ) ;for( int i = 1 ; i <= n ; ++i ){
for( int j = 1 ; j <= m ; ++j ){
cin >> mi[++cnt].z ;mi[cnt].x = i ;mi[cnt].y = j ;b[i][j] = mi[cnt].z ;}}sort( mi + 1 , mi + 1 + cnt , cmp ) ;for( int i = 1 ; i <= m ; ++i ){
a[mi[i].x][i] = mi[i].z ;vis[mi[i].x][mi[i].y] = 1 ;}for( int i = 1 ; i <= n ; ++i ){
q = 0 ;for( int j = 1 ; j <= m ; ++j ){
if( !vis[i][j] )v[i][++q] = b[i][j] ; }}for( int i = 1 ; i <= n ; ++i ){
q = 0 ;for( int j = 1 ; j <= m ; ++j ){
if( !a[i][j] )a[i][j] = v[i][++q] ;}}for( int i = 1 ; i <= n ; ++i ){
for( int j = 1 ; j <= m ; ++j )cout << a[i][j] << " \n"[j==m] ;}}return 0 ;
}