当前位置：代码迷 >> 综合 >> MIT 线性代数 1-5讲总结：消元、主元、初等矩阵、不可逆矩阵的证明、高斯-约尔当求逆、上下三角矩阵、置换矩阵、转置、向量空间与子空间

详细解决方案

MIT 线性代数 1-5讲总结：消元、主元、初等矩阵、不可逆矩阵的证明、高斯-约尔当求逆、上下三角矩阵、置换矩阵、转置、向量空间与子空间

热度：29 发布时间：2023-11-22 20:03:36.0

1.增广矩阵

系数矩阵右边加一列（线性方程组的解）

2.消元与主元

主元(图中绿色圈中的元素)：消元的关键，不能为0，为0则需行变换改变主元

3.初等矩阵

通过将n倍的某行加到令一行达到消元的目的

而这种手段也是通过矩阵乘法进行的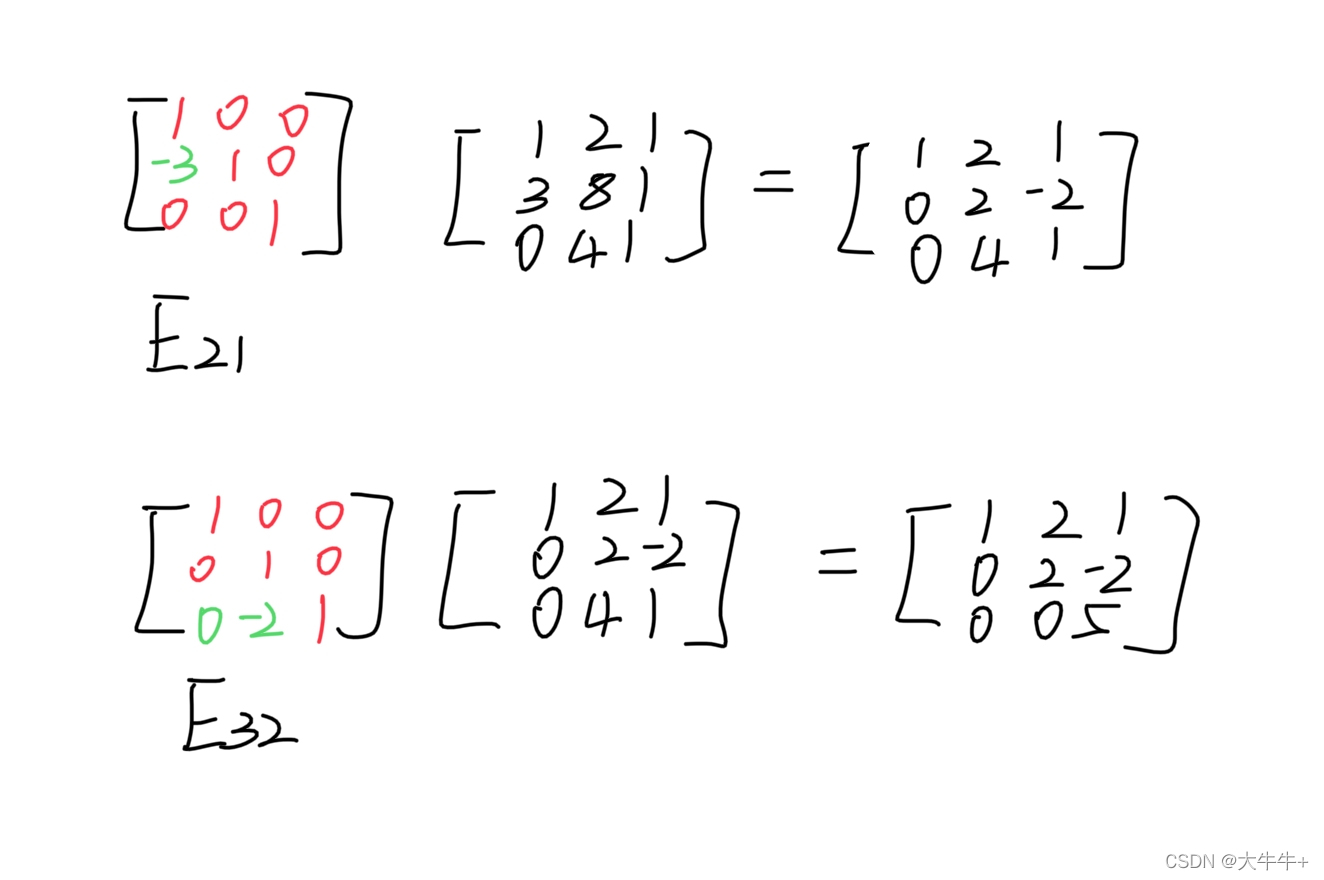

E:element matrix:初等矩阵

$E_{nm}$ :将原矩阵第n行m列的元素归零需要的矩阵

红色部分为固定的，绿色部分为需要考虑的

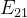$E_{21}$ :为了将2行1列的元素归零，我们需要利用本行前面行的元素来清除他（第二行前面的行只有第一行，因此只有一个能考虑的）

第一行：1 0 0：数字n为需要原矩阵n个第几行：需要1个第一行，0个第二行和第三行

第二行：-3 1 0：需要1个第二行，-3个第一行和0个第三行

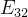$E_{32}$ :将第3行第2列元素清零可用前两行（即两个绿色元素）

初始矩阵的融合

由乘法结合律可将两初始矩阵二合为一

$E_{32}(E_{21}A)=U$ $(E_{32}E_{21})A=U$ $EA=U$

4.矩阵的乘法

1.将矩阵B分解为列，矩阵A分别与矩阵B的所有列相乘，最后将所得合并

2.矩阵B分解为行，矩阵A分别与矩阵B所有行相乘最后合并（与1类似）

3.初始矩阵的乘法：左矩阵当初始矩阵， $a_{32}$ ：得出的结果的第三行需要原始矩阵的 $a_{32 }$ 个第二行

4.一个个元素计算：答案的第ij个元素(1x1)为第i行的元素(1xm)乘第j列的元素(mx1)

5.矩阵的逆

矩阵与他的逆相乘为单位矩阵： $A^{-1}A=I$

不可逆矩阵（奇异矩阵）的证明

$\begin{bmatrix} 1 &3 \\ 2& 6 \end{bmatrix}$ 矩阵A，取一x使得Ax=0 即x= $\begin{bmatrix} 3\\ -1 \end{bmatrix}$

若A有逆则 $A^{-1}Ax=x$ ，但 $0 A^{-1}!= x$

高斯-约尔当公式求逆

AB的逆为： $B^{-1}A^{-1}$

$(AB)(B^{-1}A^{-1})=I$

$A(BB^{-1})A^{-1}=I$

$AA^{-1}=I$

6.A=LU

因为： $E_{32}E_{21}A=U$ 所以： $A=E_{21}^{-1}E_{32}^{-1}U$ 所以： $E_{21}^{-1}E_{32}^{-1}=L$

L：下三角矩阵 U：上三角矩阵 D（diagonal）：对角矩阵

7.置换矩阵（permutation）

行重新排列的单位矩阵，n阶矩阵的置换矩阵的个数为n!

例：三阶矩阵的所有置换矩阵 6种

$\begin{bmatrix} 1 & 0 &0 \\ 0& 1&0 \\ 0&0 & 1 \end{bmatrix}$ $\begin{bmatrix} 0 & 1 &0 \\ 1& 0&0 \\ 0&0 & 1 \end{bmatrix}$ $\begin{bmatrix} 0 & 0 &1 \\ 1& 0&0 \\ 0&1 & 0 \end{bmatrix}$

$\begin{bmatrix} 1 & 0 &0 \\ 0& 0&1 \\ 0&1 & 0 \end{bmatrix}$ $\begin{bmatrix} 0 & 1 &0 \\ 0& 0&1 \\ 1&0 & 0 \end{bmatrix}$ $\begin{bmatrix} 0 & 0 &1 \\ 0& 1&0 \\ 1&0 & 0 \end{bmatrix}$

定义： $P^{-1}=P^{T}$ $P^{T}P=I$

8.转置(transpose)

$(A^{T})_{ij}=A_{ji}$

对称矩阵（symmetric matrix)： $A^{T}=A$

9.向量空间与子空间

向量空间内的向量必须满足向量加法（向量空间内两向量相加仍在该向量空间内）与向量乘法（向量空间内某向量×一个标量，其仍在该向量空间中）

以二维空间举例：

向量a：（2，3）向量b：（1，4）

a+b=（3，7）仍在向量空间（二维空间）内，5a=（10，15）仍在向量空间内

线性组合：a+b、5a即为两个线性组合

子空间（subspace）：子空间为向量空间的子集，本身也为向量空间

二维空间子空间：1.二维空间本身 2.穿过原点的直线 3.原点本身

穿过原点的直线：直线上的任何向量相加都仍处在直线上，任何向量与任何系数相乘都在直线上（与0相乘则为(0,0)向量，所以必须过原点）

原点本身：只有一个向量(0,0)，相加为(0,0),乘任何系数也为(0,0)

三维空间的子空间：1.三维空间本身，2.过原点的平面，3.过原点的线，4.原点

相关解决方案