数学知识：快速幂

前言

复习acwing算法基础课的内容，本篇为讲解数学知识：快速幂，关于时间复杂度：目前博主不太会计算，先鸽了，日后一定补上。

一、快速幂

所谓快速幂就是用很短的时间去解决a^b % c，解决这类的问题，最传统的做法就是循环暴力枚举，但是一旦我们的范围在1e8+，这种暴力的枚举显然会TLE，这也是快速幂算法的独到之处.

二、例题，代码

AcWing 875. 快速幂

本题链接：AcWing 875. 快速幂
本博客提供本题截图：

本题解析

我们把a^b中的b当成它的二进制去考虑这个题，这里举一个例子，比如说是a^(1001)2，这样我们就可以按照如下图的方法去计算它的值：

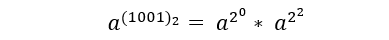
这就是快速幂的核心思想

AC代码

#include <cstdio>
#include <algorithm>using namespace std;typedef long long LL;LL qmi(int a, int b, int p)
{
    LL res = 1;while (b){
    if (b & 1) res = res * a % p; //快速幂b >>= 1;                   	  //每次都把b向右移动一个二进制长度a = (LL)a * a % p;            //每次都把a平方}return res;
}int main()
{
    int n;scanf("%d", &n);while (n -- ){
    int a, b, p;scanf("%d%d%d", &a, &b, &p);printf("%lld\n", qmi(a, b, p));}return 0;
}

AcWing 876. 快速幂求逆元

本题链接：AcWing 876. 快速幂求逆元
本博客提供本题截图：

本题解析

本题其实就是去求a^(p - 2) mol p，注意如果a % p == 0的情况是无解的，输出impossible

AC代码

#include <iostream>
#include <algorithm>using namespace std;typedef long long LL;LL qmi(int a, int b, int p)
{
    LL res = 1;while (b){
    if (b & 1) res = res * a % p;a = a * (LL)a % p;b >>= 1;}return res;
}int main()
{
    int n;scanf("%d", &n);while (n -- ){
    int a, p;scanf("%d%d", &a, &p);if (a % p == 0) puts("impossible");else printf("%lld\n", qmi(a, p - 2, p));}return 0;
}

三、时间复杂度

关于快速幂各步操作的时间复杂度以及证明，后续会给出详细的说明以及证明过程，目前先鸽了。