数学知识：求组合数

---

前言

复习acwing算法基础课的内容，本篇为讲解数学知识：求组合数，关于时间复杂度：目前博主不太会计算，先鸽了，日后一定补上。

---

一、组合数

---

二、例题，代码

AcWing 885. 求组合数 I

本题链接：AcWing 885. 求组合数 I
本博客提供本题截图：

本题解析

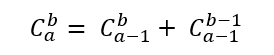
AC代码

#include <iostream>using namespace std;const int N = 2010;
const int INF = 1e9 + 7;int c[N][N];void init()
{
    for (int i = 0; i < N; i ++ )for (int j = 0; j <= i; j ++ )if (!j) c[i][j] = 1;else c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % INF;
}int main()
{
    init();int n;cin >> n;while (n -- ){
    int a, b;cin >> a >> b;cout << c[a][b] << endl;}return 0;
}

AcWing 886. 求组合数 II

本题链接：AcWing 886. 求组合数 II
本博客提供本题截图：

本题解析

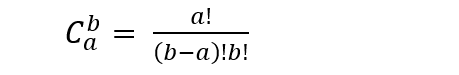
我们知道直接进行除法的话会有精度问题，所以我们可以用逆元去求解，关于逆元的求法见：数学知识：快速幂

AC代码

#include <iostream>
#include <algorithm>using namespace std;typedef long long LL;const int N = 100010, mod = 1e9 + 7;int fact[N], infact[N];int qmi(int a, int k, int p)
{
    int res = 1;while (k){
    if (k & 1) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1;}return res;
}int main()
{
    fact[0] = infact[0] = 1;for (int i = 1; i < N; i ++ ){
    fact[i] = (LL)fact[i - 1] * i % mod;infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;}int n;scanf("%d", &n);while (n -- ){
    int a, b;scanf("%d%d", &a, &b);printf("%d\n", (LL)fact[a] * infact[b] % mod * infact[a - b] % mod);}return 0;
}

AcWing 887. 求组合数 III

本题链接：AcWing 887. 求组合数 III
本博客提供本题截图：

本题解析

卢卡斯定理：

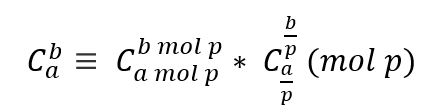
我们知道直接进行除法的话会有精度问题，所以我们可以用逆元去求解，关于逆元的求法见：数学知识：快速幂

AC代码

#include <iostream>
#include <algorithm>using namespace std;typedef long long LL;int qmi(int a, int k, int p)
{
    int res = 1;while (k){
    if (k & 1) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1;}return res;
}int C(int a, int b, int p)
{
    if (b > a) return 0;int res = 1;for (int i = 1, j = a; i <= b; i ++, j -- ){
    res = (LL)res * j % p;res = (LL)res * qmi(i, p - 2, p) % p;}return res;
}int lucas(LL a, LL b, int p)
{
    if (a < p && b < p) return C(a, b, p);return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}int main()
{
    int n;cin >> n;while (n -- ){
    LL a, b;int p;cin >> a >> b >> p;cout << lucas(a, b, p) << endl;}return 0;
}

AcWing 888. 求组合数 IV

本题链接：AcWing 888. 求组合数 IV
本博客提供本题截图：

本题解析

这个题就是直接硬算，利用公式直接展开进行计算，注意本题需要用到高精度乘法，高精度乘法的模板见：高精度运算，展开方式如下图：

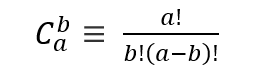
展开的过程中注意化简：我们把分母和分子使用分解质因数的形式进行化简，分解质因数见：数学知识：质数

AC代码

#include <iostream>
#include <algorithm>
#include <vector>using namespace std;const int N = 5010;int primes[N], cnt;
int sum[N];
bool st[N];void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ ){
    if (!st[i]) primes[cnt ++ ] = i;for (int j = 0; primes[j] <= n / i; j ++ ){
    st[primes[j] * i] = true;if (i % primes[j] == 0) break;}}
}int get(int n, int p)
{
    int res = 0;while (n){
    res += n / p;n /= p;}return res;
}vector<int> mul(vector<int> a, int b)
{
    vector<int> c;int t = 0;for (int i = 0; i < a.size(); i ++ ){
    t += a[i] * b;c.push_back(t % 10);t /= 10;}while (t){
    c.push_back(t % 10);t /= 10;}return c;
}int main()
{
    int a, b;cin >> a >> b;get_primes(a);for (int i = 0; i < cnt; i ++ ){
    int p = primes[i];sum[i] = get(a, p) - get(a - b, p) - get(b, p);}vector<int> res;res.push_back(1);for (int i = 0; i < cnt; i ++ )for (int j = 0; j < sum[i]; j ++ )res = mul(res, primes[i]);for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);puts("");return 0;
}

AcWing 889. 满足条件的01序列

本题链接：AcWing 889. 满足条件的01序列
本博客提供本题截图：

本题解析

我们拿样例去分析，样例3的含义就是给你3个0和3个1，假设有这么一幅图：

我们规定0是往右走，1是向上走一格，按照样例的要求，我们需要向右走三格，向上走三格，那么，不管我们怎么去选择走的方法（0和1的次序），我们的最终都会走到点（3, 3），题中的要求为求它们能排列成的所有序列中，能够满足任意前缀序列中 0 的个数都不少于 1 的个数，即我们需要满足我们路径中任何一个点都不可以超过或碰到如下图所示的红线：

如图，我们的橙色的线条对应的就是一条正确的路线，而蓝色的线条对应的就是一条错误的路线，接着，我们把蓝线第一个接触到红线的点(1,2)开始，其后图像做关于红线对称，可得到绿线如下图所示：

我们不难知道，只要我们有违规的线条（比如上图所示的蓝色的线），在经过上述得到绿线后，最终到达的点都是点(2,4)，即本题结果为：

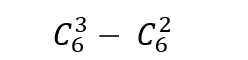
由特殊到一般，对于每一个n，都有结果为

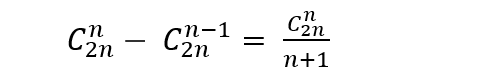
AC代码

#include <iostream>
#include <algorithm>using namespace std;typedef long long LL;const int N = 100010, mod = 1e9 + 7;int qmi(int a, int k, int p)
{
    int res = 1;while (k){
    if (k & 1) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1;}return res;
}int main()
{
    int n;cin >> n;int a = n * 2, b = n;int res = 1;for (int i = a; i > a - b; i -- ) res = (LL)res * i % mod;for (int i = 1; i <= b; i ++ ) res = (LL)res * qmi(i, mod - 2, mod) % mod;res = (LL)res * qmi(n + 1, mod - 2, mod) % mod;cout << res << endl;return 0;
}

---

三、时间复杂度

关于求组合数各步操作的时间复杂度以及证明，后续会给出详细的说明以及证明过程，目前先鸽了。