算法题！求解解决方法

算法题！！！求解
输入一张图： 


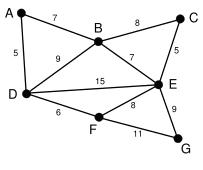
说明：边的数值代表从A到B的代价；

输出：从a到G的路线，要求，代价最小：

求解：算法：
1
先随便输出5条路径：
比如：abeg adbeg  adfg  abceg  adefg
2，计算每条路径的健康度：也就是花费：
比如：abeg＝7+7+9；
3，选出5条中最健康的4条。两两进行交配。

交配就是如果有相同节点，则交换路径：
比如：
abc  d  efg
afscv d   fdsg

他们俩交换以后是
afscv  d  efg
abc d   fdsg

然后在计算这四条的健康度。

以此类推。直到只有一条思想本身就不是最权威的，而且，这种问题最好自己去实现，不要总是想着用别人提供好的API，虽然咱身为码工，但是一定要有成为设计人员的目标。
试试用迪杰斯特拉算法，参考http://baike.baidu.com/view/1939816.htm。
基本思想：
将图G中所有的顶点V分成两个顶点集合S和T。以v为源点已经确定了最短路径的终点并入S集合中，S初始时只含顶点v,T则是尚未确定到源点v最短路径的顶点集合。然后每次从T集合中选择S集合点中到T路径最短的那个点，并加入到集合S中，并把这个点从集合T删除。直到T集合为空为止。 
首先，你要明白“图”是点的集合与关系的集合这两个集合组合在一起的数据结构，而“邻接表”是最常用的描述无向图或者有向图的方法
图论算法我研究过一段时间，所以这里就把我写的代码直接贴上去了，会有一些用不到的代码，请大家见谅：
迪杰斯特拉算法的类，对照这个类来看下面三个类吧！

package tm.cao.tu;

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
//专门用于迪杰斯特拉算法的类 

public class Dijkstra{
	//顶点集合
	private List<DingDian> dianList;
	//关系集合
	private List<GuanXi> guanxiList;
	public List<DingDian> getDianList() {
		return dianList;
	}
	public List<GuanXi> getGuanxiList() {
		return guanxiList;
	}
	public void setDianList(List<DingDian> dianList) {
		this.dianList = dianList;
	}
	public void setGuanxiList(List<GuanXi> guanxiList) {
		this.guanxiList = guanxiList;
	}
	//构造器
	public Dijkstra(List<DingDian> dianList, List<GuanXi> guanxiList, Integer flag) {
		super();
		this.dianList = dianList;
		//有向图
		if(flag==0){
			this.guanxiList=guanxiList;
		}else if(flag==1){
			//如果是无向图，则需要加入反序的关系
			List<GuanXi> list2=new ArrayList<GuanXi>();
			for(GuanXi gx:guanxiList){
				GuanXi fan=new GuanXi(gx.getWei(), gx.getTou(), gx.getQuan());
				list2.add(fan);
			}
			guanxiList.addAll(list2);
			this.guanxiList=guanxiList;
		}else{
			//无论如何也不扩展边集  相当于只创建边集数组
			this.guanxiList=guanxiList;
		}
	}


//构造邻接表
public void createLingJieBiao(){
	if(guanxiList.size()>0){
		Collections.sort(guanxiList);
	}
	for(GuanXi gx:guanxiList){
		DingDian tou=gx.getTou();
		Hu q=new Hu(gx.getWei(), gx.getQuan());
		q.setId(gx.getId());
		//入度+1 对应于拓扑排序
		DingDian wei=gx.getWei();
		int rudu=wei.getRudu();
		rudu++;
		wei.setRudu(rudu);
		if(tou.getFirstHu()==null){
			tou.setFirstHu(q);
		}else{
			Hu p=tou.getFirstHu();
			while(p.getNextHu()!=null){
				p=p.getNextHu();
			}
			p.setNextHu(q);
		}
	}
}
/**迪杰斯克拉算法  http://baike.baidu.com/view/1939816.htm
 *sList:需要求的顶点集合 一开始只有一个点 dist属性：记录长度，path属性：记录路径的数组
 */
public List<DingDian> disjaktra(DingDian which){
	this.createLingJieBiao();
	List<DingDian> sList=new ArrayList<DingDian>();
	//为了计算dist方便 设置一个动态集合 用于记录dist已经不是null的点
	List<DingDian> dongtaiList=new ArrayList<DingDian>();