机器学习（3）：局部加权线性回归算法、Logistic回归算法

前言：本节记录STANFORD机器学习课程（Andrew Ng主讲），第3课学习笔记。

               第1、2课请看：机器学习（一、二）：批梯度下降法、随机/增量梯度下降法、最小二乘法

简介：在本节中，介绍局部加权线性回归算法（Loess/LWR）和Logistic回归算法。

一：局部加权线性回归

假设有一组数据是这样的：

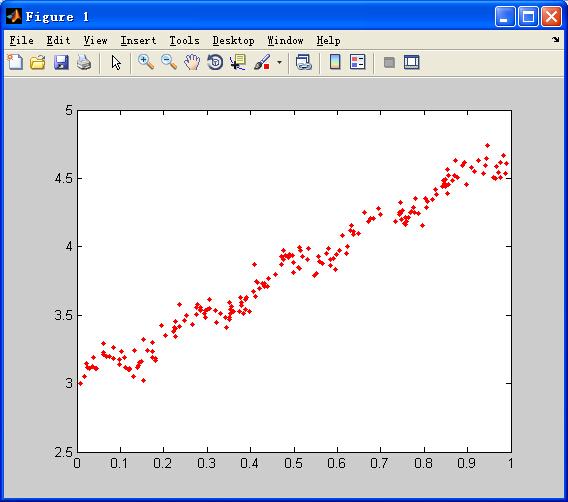
根据上一节线性回归算法，最小二乘法结果为：

局部加权线性回归算法，是一种非参数学习法（non-parametric）：

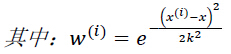
        对于上述公式的理解是这样的：x为某个预测点，x^((i))为样本点，样本点距离预测点越近，贡献的误差越大（权值越大），越远则贡献的误差越小（权值越小）。关于预测点的选取，在我的代码中取的是样本点。其中k是带宽参数，控制w（钟形函数）的宽窄程度，类似于高斯函数的标准差。

        算法思路：假设预测点取样本点中的第i个样本点（共m个样本点），遍历1到m个样本点（含第i个），算出每一个样本点与预测点的距离，也就可以计算出每个样本贡献误差的权值，可以看出w是一个有m个元素的向量（写成对角阵形式），代入上式J(θ)中。

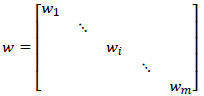
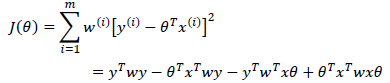
利用最小二乘法，可以计算出一个θ向量（一个预测点对应一个向量）

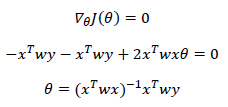
如此下去，i从1取到m，就可以计算出m个θ向量。

MATLAB代码如下：

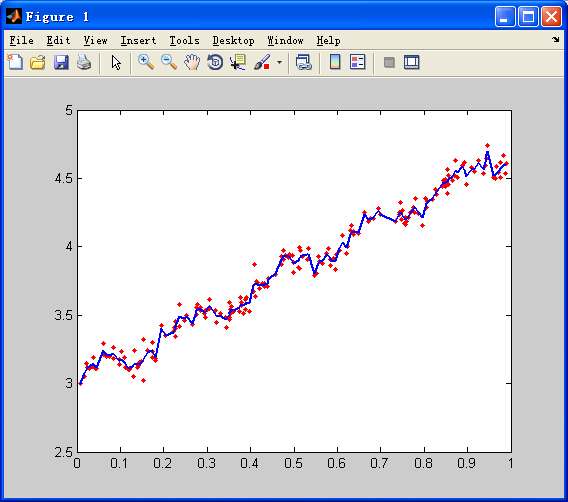
%局部加权线性回归算法（LWR/LOESS）clc;clear all;close all;%%%载入数据%load ('data1.mat');load ('data2.mat');%load ('data3.mat');x=data(:,1:2);y=data(:,3);%%m=size(x,1);%样本数n=size(x,2);%特征维数k=0.1;w=zeros(m,m);theta=zeros(n,m);for i=1:m    for j=1:m        w(j,j)=exp(-((x(i,2)-x(j,2))^2)/(2*k^2));    end    theta(:,i)=((x'*w*x)\x')*w*y;endfigure;plot(x(:,2),y,'r.');%原始数据hold on;y_fit=x*theta;y=diag(y_fit);data(:,1:2)=x;data(:,3)=y;data=sortrows(data,2);x=data(:,1:2);y=data(:,3);plot(x(:,2),y);%完

当然，局部加权线性回归算法存在欠拟合和过拟合问题。

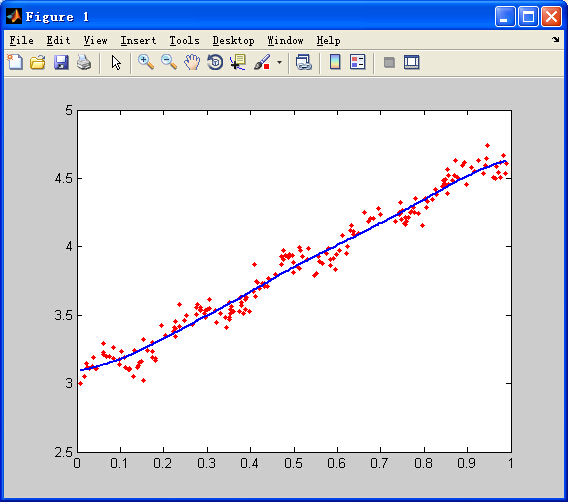
k=0.1

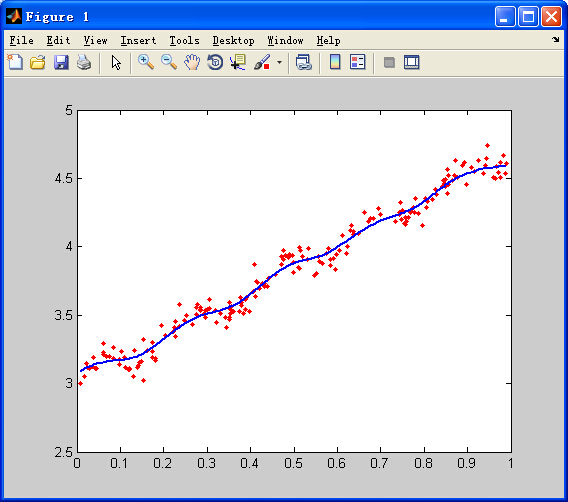
k=0.05

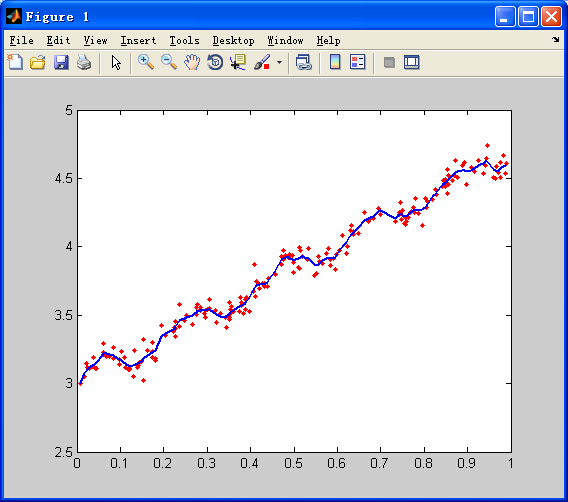
k=0.005

二、Logistic回归

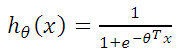
与线性回归类似，只是假设函数变成了上式的Logistic函数，而非线性函数。

求解方法类似，利用最小二乘法可求解。

MATLAB代码如下：

%Logistic回归算法clc;clear all;close all;%%load ('data5.mat');x=data(:,1:2);y=data(:,3);%%n=size(x,2);%特征维数m=size(x,1);%样本个数alpha=2.68;theta=zeros(n,1);%参数t=theta;for k=1:100    for j=1:m        for i=1:n            t(i,1)=theta(i,1)-alpha*(1/(1+exp(-(x(j,:)*theta)))-y(j,1))*x(j,i);        end        theta=t;    endendfigure;plot(x(:,2),y,'r.');%原始数据hold on;for j=1:m    y(j,1)=1/(1+exp(-(x(j,:)*theta)));%拟合数据enddata(:,1:2)=x;data(:,3)=y;data=sortrows(data,2);x=data(:,1:2);y=data(:,3);plot(x(:,2),y);for i=1:n    fprintf('theta%d=%f;\n',i-1,theta(i,1));%打印估计的参数end%完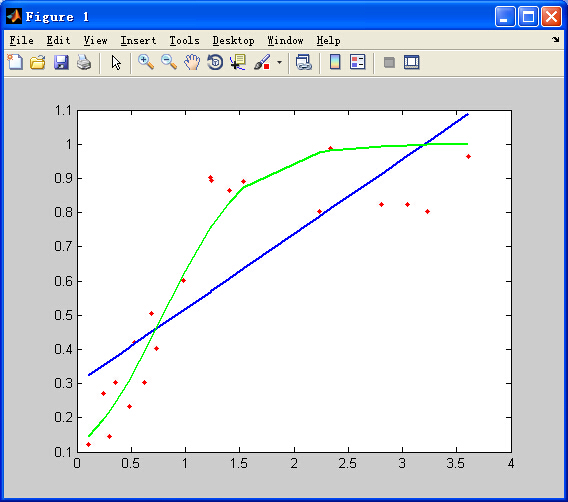

实验数据已上传，此处下载：http://download.csdn.net/detail/hujingshuang/8754931